R でダネットのテストを実行する方法

事後検定は、どのグループの平均値が互いに統計的に有意に異なるかを決定するために、 ANOVAの後に実行される検定の一種です。

研究グループの 1 つが対照グループとみなされる場合は、 ダネットの検定を事後検定として使用する必要があります。

このチュートリアルでは、R でダネット テストを実行する方法について説明します。

例: R でのダネット テスト

教師が 2 つの新しい学習テクニックが生徒のテストの成績を向上させる可能性があるかどうか知りたいと考えているとします。これをテストするために、彼女は 30 人の生徒のクラスを次の 3 つのグループにランダムに分割しました。

• 対照群: 10 人の学生
• 新しい技術学習 1: 学生 10 名
• 新技術学習2：10名

割り当てられた学習方法を 1 週間使用した後、各生徒は同じ試験を受けます。

R で次の手順を使用して、データセットを作成し、グループ平均を視覚化し、一元配置分散分析を実行し、最後にダネット検定を実行して、どの新しい研究手法 (存在する場合) が対照グループと比較して異なる結果を生み出すかを判断できます。 。

ステップ 1: データセットを作成します。

次のコードは、30 人の学生全員の試験結果を含むデータセットを作成する方法を示しています。

 #create data frame
data <- data.frame(technique = rep (c("control", "new1", "new2"), each = 10 ),
                   score = c(76, 77, 77, 81, 82, 82, 83, 84, 85, 89,
                             81, 82, 83, 83, 83, 84, 87, 90, 92, 93,
                             77, 78, 79, 88, 89, 90, 91, 95, 95, 98))

#view first six rows of data frame
head(data)

  technical score
1 control 76
2 controls 77
3 controls 77
4 controls 81
5 controls 82
6 controls 82

ステップ 2: 各グループの試験結果を表示します。

次のコードは、箱ひげ図を作成して各グループの検査結果の分布を視覚化する方法を示しています。

 boxplot(score ~ technique,
        data = data,
        main = "Exam Scores by Studying Technique",
        xlab = "Studying Technique",
        ylab = "Exam Scores",
        col = "steelblue",
        border = "black")

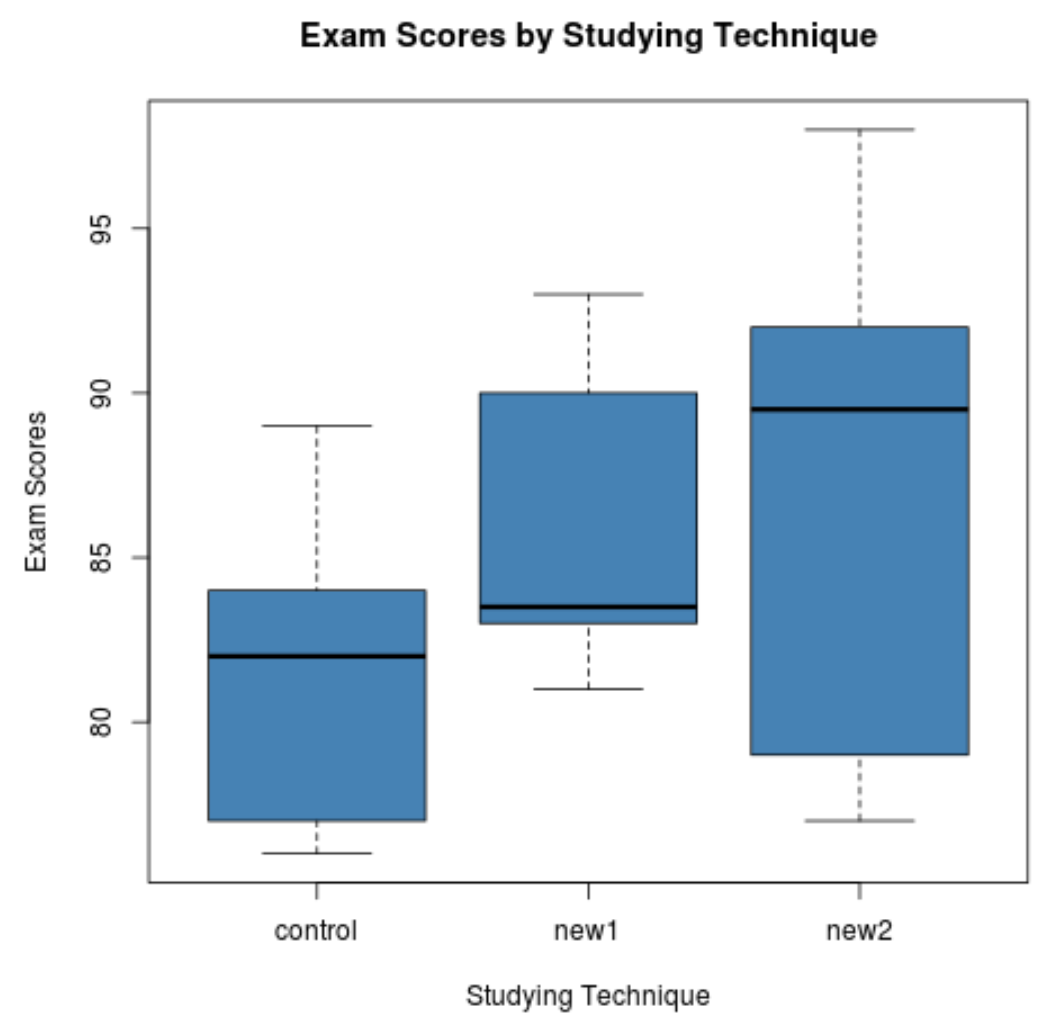
箱ひげ図からだけでも、試験の得点の分布が学習手法ごとに大きく異なることがわかります。次に、一元配置分散分析を実行して、これらの違いが統計的に有意であるかどうかを判断します。

関連: R で単一のグラフに複数の箱ひげ図をプロットする方法

ステップ 3: 一元配置分散分析を実行します。

次のコードは、一元配置分散分析を実行して、各グループの平均試験得点間の差異をテストする方法を示しています。

 #fit the one-way ANOVA model
model <- aov(score ~ technique, data = data)

#view model output
summary(model)

            Df Sum Sq Mean Sq F value Pr(>F)  
technical 2 211.5 105.73 3.415 0.0476 *
Residuals 27 836.0 30.96                 
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

全体の p 値 ( 0.0476 ) は 0.05 未満であるため、これは各グループの試験平均点が同じではないことを示しています。次に、ダネット テストを実行して、どの勉強法が対照群と異なる試験の平均点をもたらしたかを判断します。

ステップ 4: ダネット テストを実行します。

R で Dunnett テストを実行するには、次の構文を使用するDescToolsライブラリのDunnettTest()関数を使用できます。

ダネット検定(x, g)

金：

• x:データ値の数値ベクトル (試験結果など)
• g:グループの名前を指定するベクトル (例: 学習テクニック)

次のコードは、この例でこの関数を使用する方法を示しています。

 #load DescTools library
library(DescTools)

#perform Dunnett's Test
DunnettTest(x=data$score, g=data$technique)

  Dunnett's test for comparing several treatments with a control:  
    95% family-wise confidence level

$control
             diff lwr.ci upr.ci pval    
new1-control 4.2 -1.6071876 10.00719 0.1787    
new2-control 6.4 0.5928124 12.20719 0.0296 *  

---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1' '1.' 0.1 ' ' 1

結果を解釈する方法は次のとおりです。

• 新しい勉強法 1 と対照群の試験得点の平均差は4.2 でした。対応する p 値は0.1787です。
• 新しい勉強法 2 と対照群の試験得点の平均差は6.4 でした。対応する p 値は0.0296です。

結果に基づいて、テクニック 2 の学習が、対照グループの平均スコアと有意に (p = 0.0296) 異なる平均試験スコアを生み出す唯一のテクニックであることがわかります。

追加リソース

一元配置分散分析の概要
R で一元配置分散分析を実行する方法
R で Tukey テストを実行する方法