Anova の仮定を確認する方法
一元配置分散分析は、 3 つ以上の独立したグループの平均値間に有意差があるかどうかを判断するために使用される統計検定です。
一元配置分散分析を使用する場合の例を次に示します。
90 人の生徒からなるクラスを 30 人ずつの 3 つのグループにランダムに分割します。各グループは、1 か月間異なる学習テクニックを使用して試験に備えます。月末に、生徒全員が同じ試験を受けます。
勉強法が試験の成績に影響するかどうか知りたい。そこで、一元配置分散分析を実行して、3 つのグループの平均スコア間に統計的に有意な差があるかどうかを判断します。
一元配置分散分析を実行する前に、まず 3 つの仮定が満たされていることを確認する必要があります。
1. 正規性– 各サンプルは正規分布した母集団から抽出されました。
2. 等しい分散– サンプルが抽出された母集団の分散は等しい。
3. 独立性– 各グループ内の観測値は互いに独立しており、グループ内の観測値はランダムサンプリングによって取得されました。
これらの仮定が満たされない場合、一元配置分散分析の結果は信頼できない可能性があります。
この記事では、これらの前提を確認する方法と、これらの前提に違反している場合の対処方法について説明します。
仮定 #1: 正常性
ANOVA は、各サンプルが正規分布した母集団から抽出されたことを前提としています。
R でこの仮説を確認する方法:
この仮説を検証するには、次の 2 つのアプローチを使用できます。
- ヒストグラムまたはQQ プロットを使用して仮説を視覚的に検証します。
- Shapiro-Wilk、Kolmogorov-Smironov、Jarque-Barre、D’Agostino-Pearson などの正式な統計検定を使用して仮説を検証します。
たとえば、減量実験に参加する人を 90 人募集し、30 人をランダムに割り当てて、プログラム A、プログラム B、またはプログラム C のいずれかを 1 か月間実行するとします。プログラムが減量に影響を与えるかどうかを確認するために、一元配置分散分析を実行します。次のコードは、ヒストグラム、QQ プロット、および Shapiro-Wilk 検定を使用して正規性の仮定をチェックする方法を示しています。
1. ANOVA モデルを当てはめます。
#make this example reproducible
set.seed(0)
#create data frame
data <- data. frame (program = rep(c(" A ", " B ", " C "), each = 30 ),
weight_loss = c(runif(30, 0, 3),
runif(30, 0, 5),
runif(30, 1, 7)))
#fit the one-way ANOVA model
model <- aov(weight_loss ~ program, data = data)
2. 応答値のヒストグラムを作成します。
#create histogram
hist(data$weight_loss)
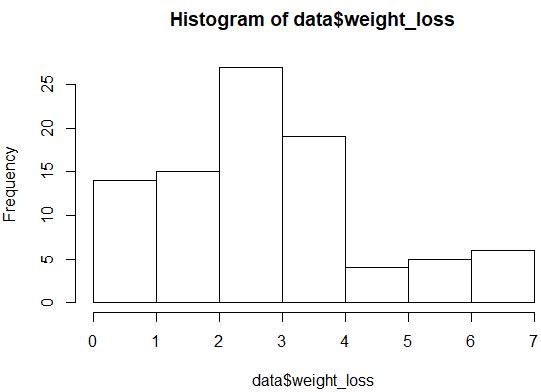
分布はあまり正規分布ではありません (たとえば、「釣鐘」の形ではありません) が、QQ プロットを作成して分布をもう一度確認することもできます。
3. 残差の QQ プロットを作成する
#create QQ plot to compare this dataset to a theoretical normal distribution qqnorm(model$residuals) #add straight diagonal line to plot qqline(model$residuals)

一般に、データ ポイントが QQ プロットの直線の対角線に沿って配置されている場合、データ セットは正規分布に従う可能性があります。この場合、端に沿った線から顕著な逸脱があることがわかります。これは、データが正規分布していないことを示している可能性があります。
4. 正規性について Shapiro-Wilk 検定を実行します。
#Conduct Shapiro-Wilk Test for normality shapiro. test (data$weight_loss) #Shapiro-Wilk normality test # #data: data$weight_loss #W = 0.9587, p-value = 0.005999
Shapiro-Wilk 検定では、サンプルが正規分布に由来しないという対立仮説に対して、サンプルが正規分布に由来するという帰無仮説を検定します。この場合、検定の p 値は0.005999で、アルファ レベルの 0.05 よりも低くなります。これは、サンプルが正規分布に従っていないことを示唆しています。
この前提が尊重されない場合はどうすればよいですか:
一般に、一元配置分散分析は、サンプル サイズが十分に大きい限り、正規性の仮定の違反に対して非常に堅牢であると考えられます。
さらに、サンプルが非常に大きい場合、シャピロ・ウィルク検定などの統計検定では、ほとんどの場合、データが正規ではないことがわかります。このため、多くの場合、ヒストグラムや QQ プロットなどのグラフを使用してデータを視覚的に検査することが最善です。グラフを見るだけで、データが正規分布しているかどうかをかなり理解できます。
正規性の前提が著しく違反されている場合、または単に非常に保守的でありたい場合には、2 つの選択肢があります。
(1)分布がより正規分布になるようにデータの応答値を変換します。
(2)正規性の仮定を必要としないクラスカル・ウォリス検定などの同等のノンパラメトリック検定を実行します。
仮定 #2: 分散が等しい
ANOVA は、サンプルの抽出元となる母集団の分散が等しいと仮定します。
R でこの仮説を確認する方法:
R では、次の 2 つのアプローチを使用してこの仮説を検証できます。
- 箱ひげ図を使用して仮説を視覚的に検証します。
- バートレット検定などの正式な統計検定を使用して仮説を検定します。
次のコードは、以前に作成したものと同じ偽の減量データセットを使用して、これを行う方法を示しています。
1. 箱ひげ図を作成します。
#Create box plots that show distribution of weight loss for each group boxplot(weight_loss ~ program, xlab=' Program ', ylab=' Weight Loss ', data=data)
各グループの体重減少の分散は、各箱ひげ図の長さによって観察できます。ボックスが長いほど、分散は大きくなります。たとえば、プログラム A およびプログラム B と比較して、プログラム C の参加者の分散がわずかに高いことがわかります。
2. バートレット テストを実行します。
#Create box plots that show distribution of weight loss for each group bartlett. test (weight_loss ~ program, data=data) #Bartlett test of homogeneity of variances # #data: weight_loss by program #Bartlett's K-squared = 8.2713, df = 2, p-value = 0.01599
バートレット検定では、サンプルの分散が等しいという帰無仮説と、サンプルの分散が等しいという対立仮説を検定します。この場合、検定の p 値は0.01599で、アルファ レベルの 0.05 よりも低くなります。これは、サンプルの分散がすべて同じではないことを示唆しています。
この前提が尊重されない場合はどうすればよいですか:
一般に、一元配置分散分析は、各グループが同じサンプル サイズである限り、等分散の仮定の違反に対してかなり堅牢であると考えられます。
ただし、サンプル サイズが同じではなく、この仮定に大きく違反する場合は、代わりに、一元配置分散分析のノンパラメトリック バージョンであるクラスカル ウォリス検定を実行できます。
前提 #3: 独立性
ANOVA は次のことを前提としています。
- 各グループの観察は、他のすべてのグループの観察から独立しています。
- 各グループ内の観察結果は、ランダムなサンプルによって得られました。
この仮説を検証する方法:
各グループの観測値が独立していること、およびそれらがランダムなサンプルによって得られたものであることを検証するために使用できる正式なテストはありません。この仮定を満たす唯一の方法は、ランダム化された設計を使用することです。
この前提が尊重されない場合はどうすればよいですか:
残念ながら、この前提が満たされない場合、できることはあまりありません。簡単に言えば、各グループの観測値が他のグループの観測値から独立していないような方法でデータが収集された場合、または各グループ内の観測値がランダム化プロセスによって取得されなかった場合、ANOVA の結果は信頼できなくなります。 。
この仮定が満たされない場合、最善の方法は、ランダム化された計画を使用して実験を再作成することです。
参考文献:
