Anova モデルで残差を分析する方法
ANOVA (「分散分析」) は、3 つ以上の独立したグループの平均間に有意な差があるかどうかを判断するために使用されるモデルの一種です。
ANOVA モデルをデータセットに当てはめると、常に残差が存在します。これらは、個々の観測値とその観測値の元となったグループ平均との差を表します。
次の例は、実際に ANOVA モデルの残差を計算する方法を示しています。
例: ANOVA での残差の計算
減量実験に参加する人を 90 人募集し、30 人をランダムに割り当てて、プログラム A、プログラム B、またはプログラム C を 1 か月間実行するとします。
一元配置分散分析を実行して、3 つのプログラムによる体重減少の間に統計的に有意な差があるかどうかを判断できます。
各プログラムに参加している人の平均体重減少を次のように計算するとします。
- プログラム A : 1.58 ポンド
- プログラム B : 2.56 ポンド
- プログラム C : 4.13 ポンド
ANOVA モデルからの残差は、各個人の体重減少とプログラムの平均体重減少の差になります。
たとえば、次の表は、研究における 10 人の異なる個人の残差を計算する方法を示しています。
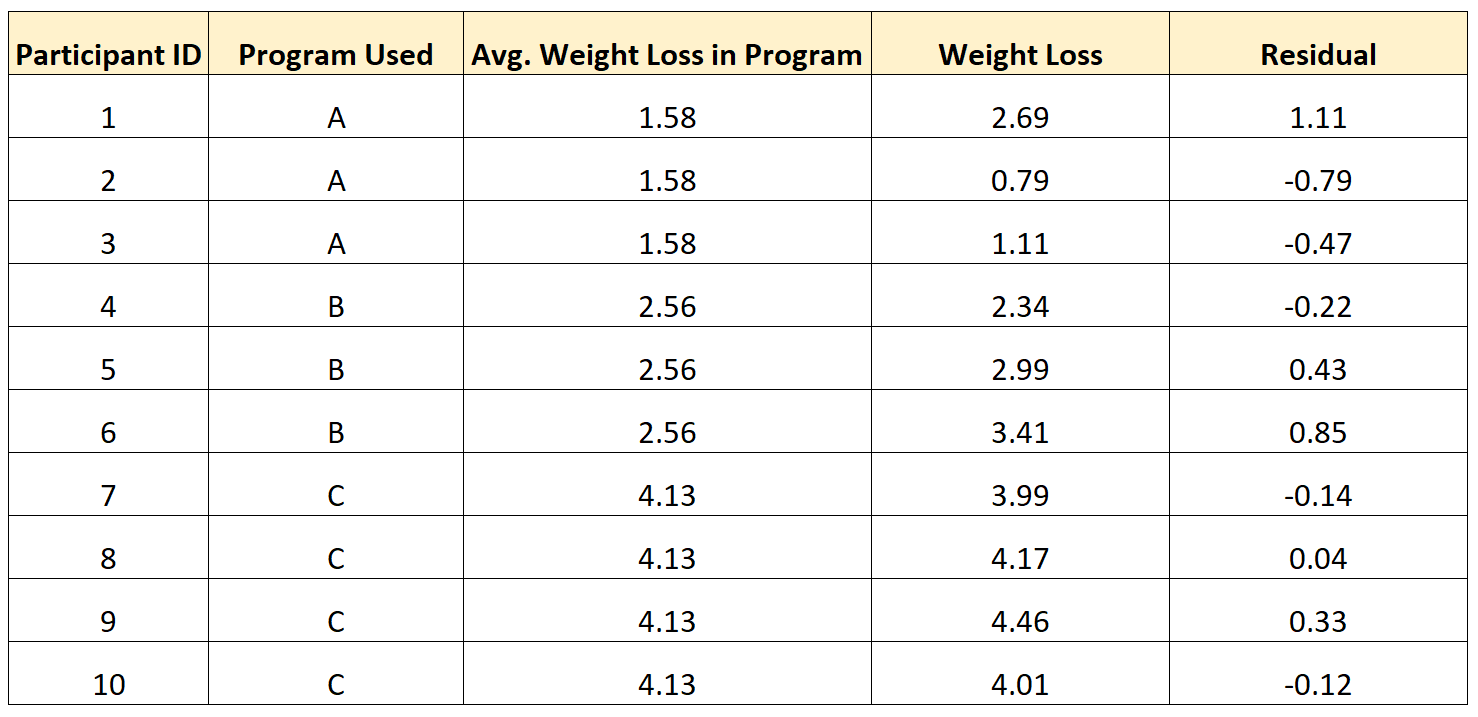
次のパターンに注意してください。
- グループ平均を超える値を持つ個人の残差は正でした。
- グループの平均値よりも低い値を持つ個人の残差は負でした。
実際には、90 人全員の残差を計算します。
残差を使用して正規性を確認する方法
ANOVA の仮定の1 つは、残差が正規分布するということです。
この仮定を検証する最も一般的な方法は、 QQ プロットを作成することです。
残差が正規分布している場合、QQ プロット上の点は直線の対角線上にあります。
前の例の QQ プロットは次のようになります。
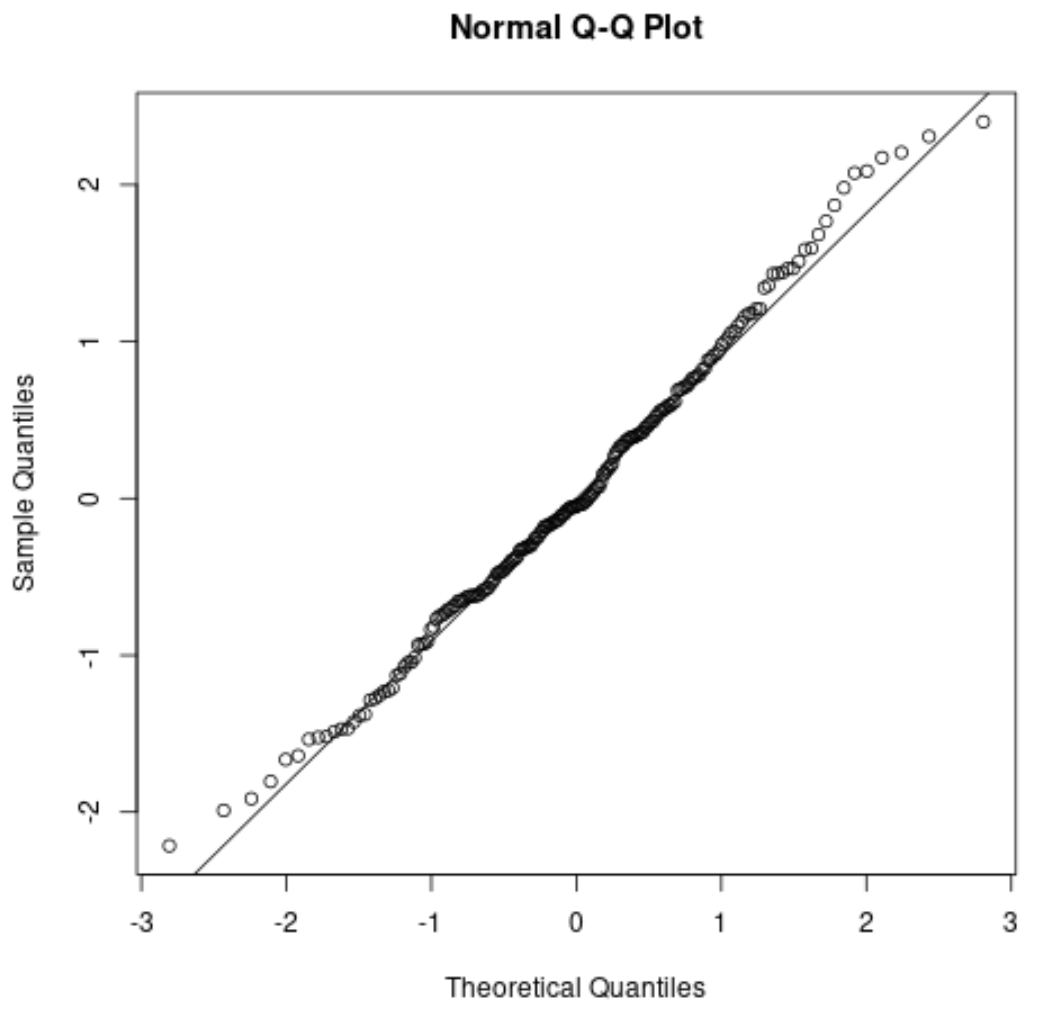
テール先端の真っすぐな対角線からティップが少しずれていますが、全体的にティップフォールは対角線によく沿っています。これは、正規性の仮定がおそらく満たされることを示しています。
参考として、非正規分布残差の QQ プロットは次のようになります。
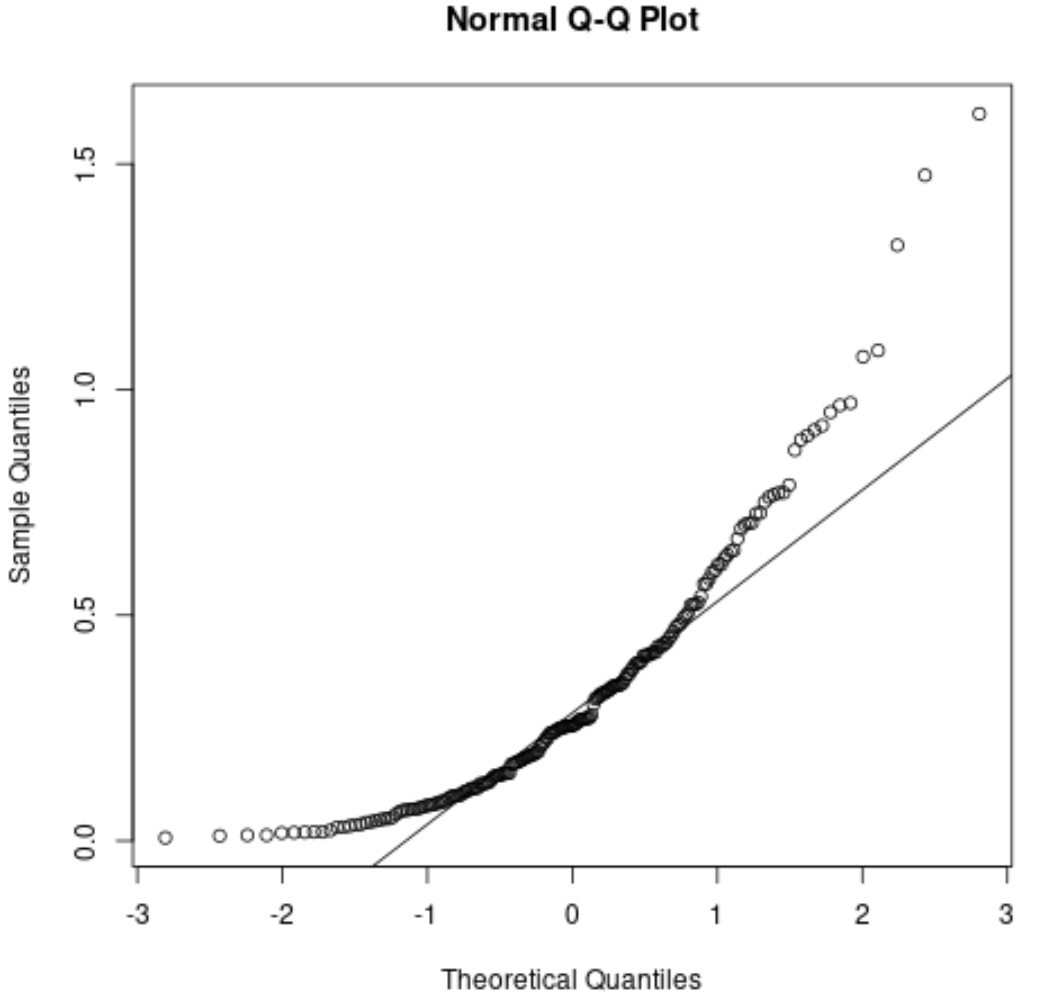
点は直線の対角線から大きく外れており、残差が正規分布していないことを示しています。
さまざまなソフトウェアで QQ プロットを作成する方法については、次のチュートリアルを参照してください。
追加リソース
次の記事では、ANOVA モデルに関する追加情報を提供します。