R でデータを変換する方法 (対数、平方根、立方根)
多くの統計検定では、 応答変数の残差が正規分布すると仮定しています。
ただし、残差は正規分布にならないことがよくあります。この問題を解決する 1 つの方法は、次の 3 つの変換のいずれかを使用して応答変数を変換することです。
1. 対数変換:応答変数を y からlog(y)に変換します。
2. 平方根変換:応答変数を y から√yに変換します。
3. 立方根変換:応答変数を y からy 1/3に変換します。
これらの変換を実行することにより、応答変数は通常、正規分布に近似します。次の例は、R でこれらの変換を実行する方法を示しています。
R でのログ変換
次のコードは、応答変数に対してログ変換を実行する方法を示しています。
#create data frame df <- data.frame(y=c(1, 1, 1, 2, 2, 2, 2, 2, 2, 3, 3, 3, 6, 7, 8), x1=c(7, 7, 8, 3, 2, 4, 4, 6, 6, 7, 5, 3, 3, 5, 8), x2=c(3, 3, 6, 6, 8, 9, 9, 8, 8, 7, 4, 3, 3, 2, 7)) #perform log transformation log_y <- log10(df$y)
次のコードは、対数変換の実行前後のyの分布を表示するヒストグラムを作成する方法を示しています。
#create histogram for original distribution hist(df$y, col='steelblue', main='Original') #create histogram for log-transformed distribution hist(log_y, col='coral2', main='Log Transformed')
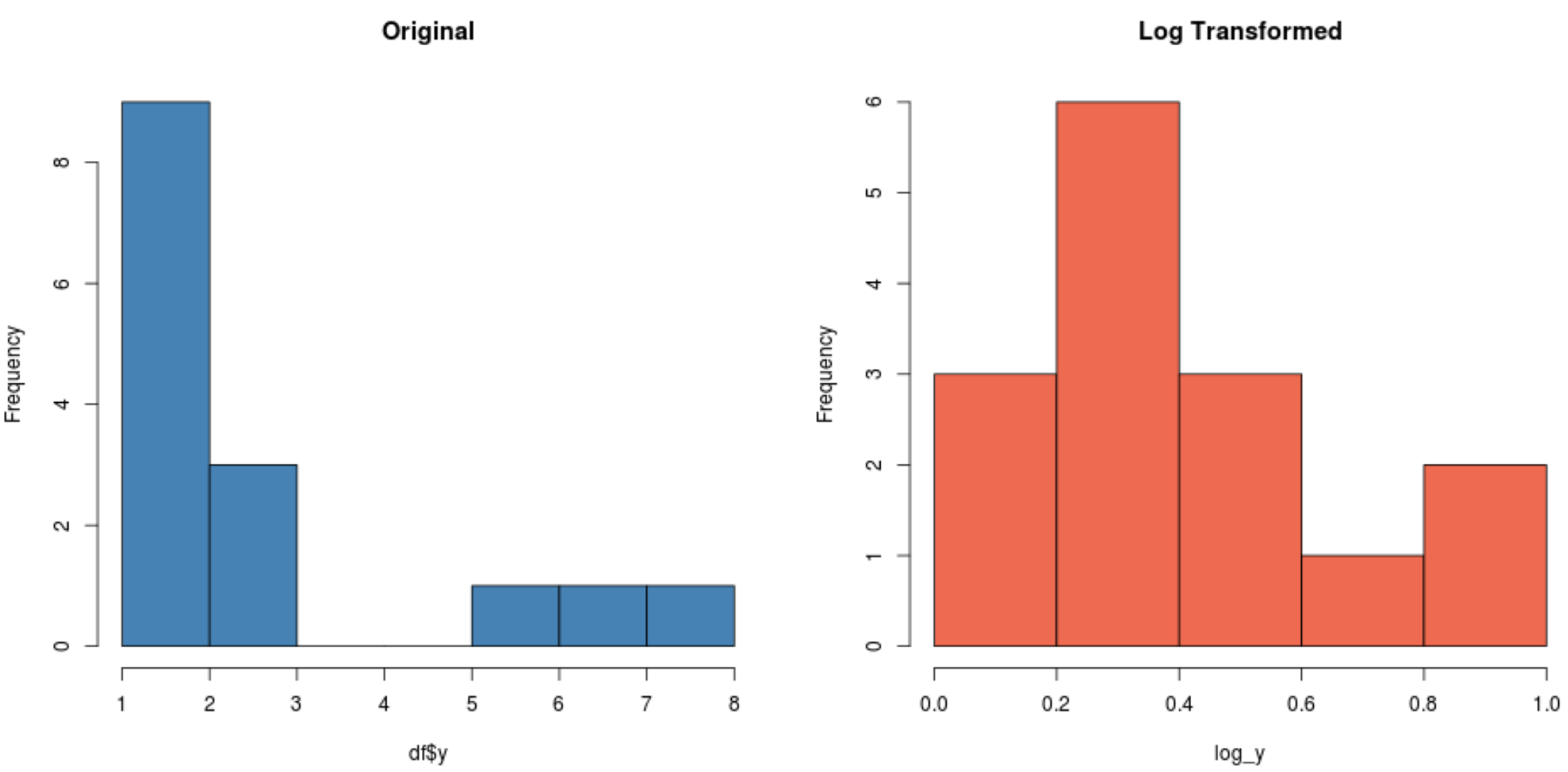
対数変換された分布が元の分布よりもはるかに正規になっていることに注目してください。まだ完全な「釣鐘型」ではありませんが、元の分布よりも正規分布に近づいています。
実際、各分布に対してShapiro-Wilk 検定を実行すると、元の分布は正規性の仮定を満たさないのに対し、対数変換された分布は正規性の仮定を満たさないことがわかります (α = 0.05)。
#perform Shapiro-Wilk Test on original data shapiro.test(df$y) Shapiro-Wilk normality test data: df$y W = 0.77225, p-value = 0.001655 #perform Shapiro-Wilk Test on log-transformed data shapiro.test(log_y) Shapiro-Wilk normality test data:log_y W = 0.89089, p-value = 0.06917
R の平方根変換
次のコードは、応答変数に対して平方根変換を実行する方法を示しています。
#create data frame df <- data.frame(y=c(1, 1, 1, 2, 2, 2, 2, 2, 2, 3, 3, 3, 6, 7, 8), x1=c(7, 7, 8, 3, 2, 4, 4, 6, 6, 7, 5, 3, 3, 5, 8), x2=c(3, 3, 6, 6, 8, 9, 9, 8, 8, 7, 4, 3, 3, 2, 7)) #perform square root transformation sqrt_y <- sqrt(df$y)
次のコードは、平方根変換を実行する前後のyの分布を表示するヒストグラムを作成する方法を示しています。
#create histogram for original distribution hist(df$y, col='steelblue', main='Original') #create histogram for square root-transformed distribution hist(sqrt_y, col='coral2', main='Square Root Transformed')
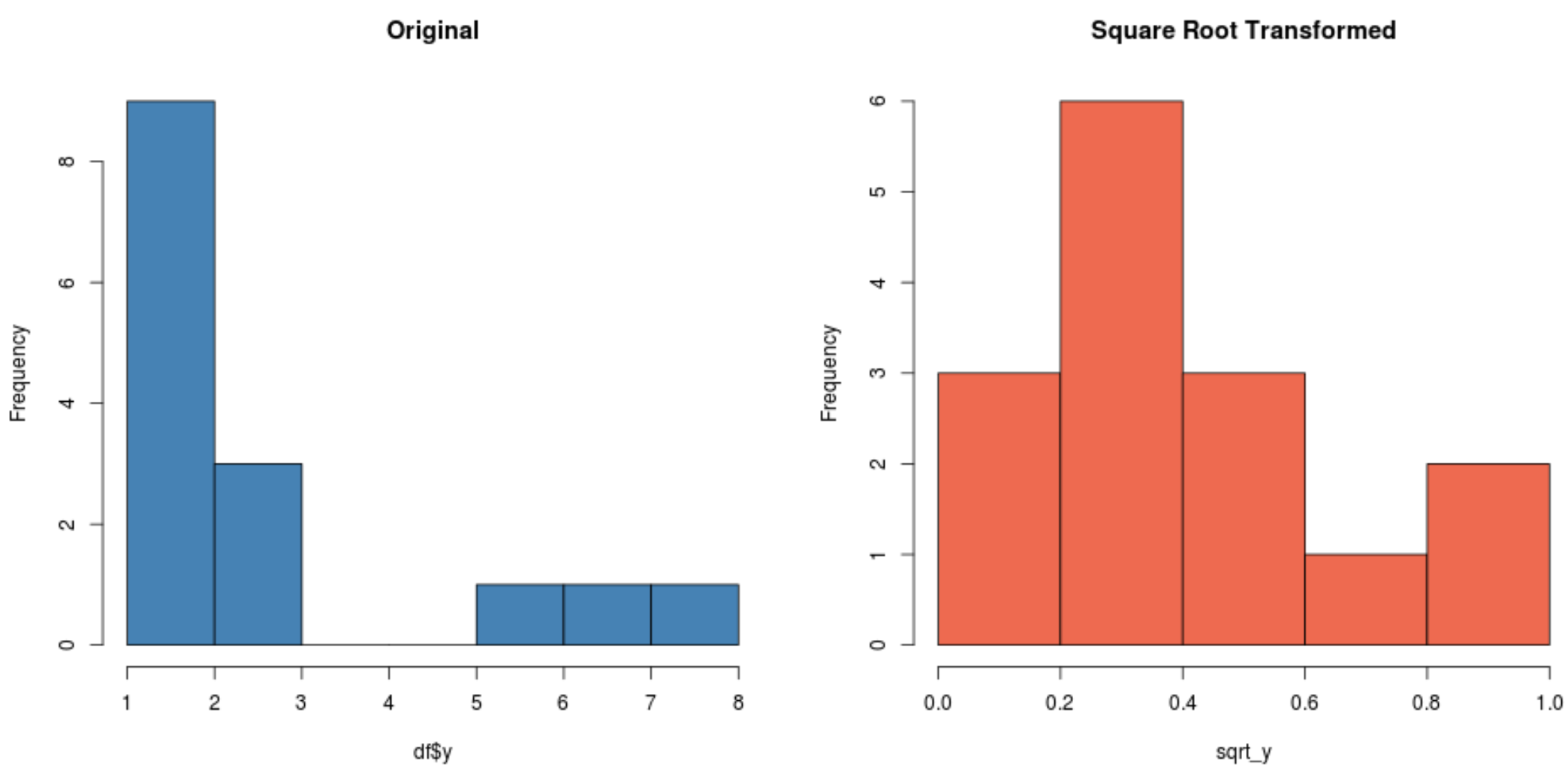
平方根変換された分布が元の分布よりもはるかに正規分布になっていることに注目してください。
R での立方根変換
次のコードは、応答変数に対して立方根変換を実行する方法を示しています。
#create data frame df <- data.frame(y=c(1, 1, 1, 2, 2, 2, 2, 2, 2, 3, 3, 3, 6, 7, 8), x1=c(7, 7, 8, 3, 2, 4, 4, 6, 6, 7, 5, 3, 3, 5, 8), x2=c(3, 3, 6, 6, 8, 9, 9, 8, 8, 7, 4, 3, 3, 2, 7)) #perform square root transformation cube_y <- df$y^(1/3)
次のコードは、平方根変換を実行する前後のyの分布を表示するヒストグラムを作成する方法を示しています。
#create histogram for original distribution hist(df$y, col='steelblue', main='Original') #create histogram for square root-transformed distribution hist(cube_y, col='coral2', main='Cube Root Transformed')
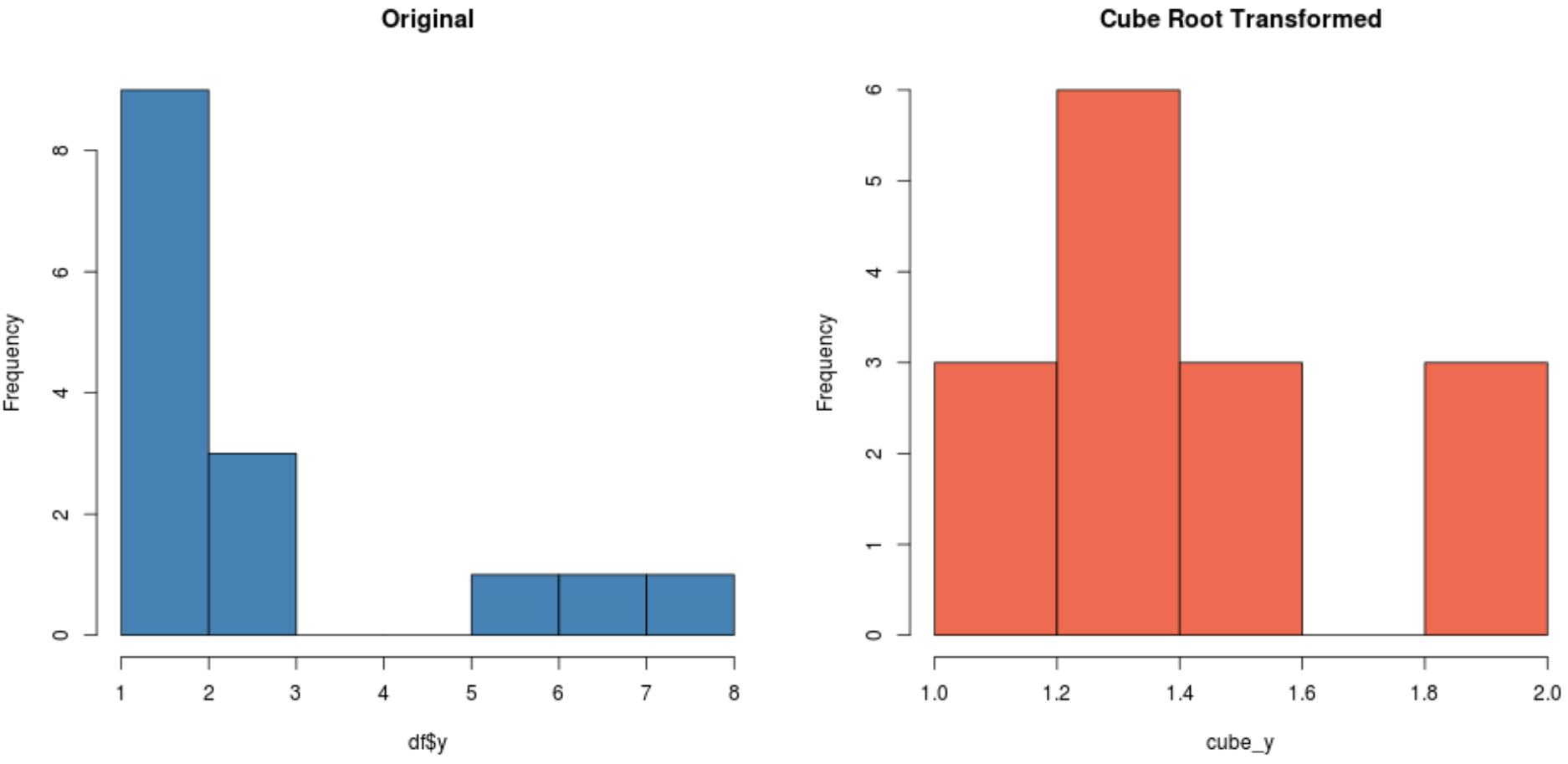
データセットによっては、これらの変換の 1 つにより、他の変換よりも正規分布の新しいデータセットが生成される場合があります。