バランスの取れた精度とは何ですか? (定義&例)

バランスの取れた精度は、分類モデルのパフォーマンスを評価するために使用できる指標です。

次のように計算されます。

バランスの取れた精度= (感度 + 特異度) / 2

金：

• 感度: 「真陽性率」 – モデルが検出できる陽性症例の割合。
• 特異度: 「真陰性率」 – モデルが検出できる陰性ケースの割合。

このメトリクスは、2 つのクラスのバランスが崩れている場合、つまり、一方のクラスが他方のクラスよりも多く表示される場合に特に役立ちます。

次の例は、実際にバランスの取れた精度を計算する方法を示し、それがなぜ非常に有用な指標であるかを示しています。

例: バランスの取れた精度の計算

スポーツ アナリストがロジスティック回帰モデルを使用して、400 人のさまざまな大学バスケットボール選手が NBA にドラフトされるかどうかを予測するとします。

次の混同行列は、モデルによって行われた予測を要約したものです。

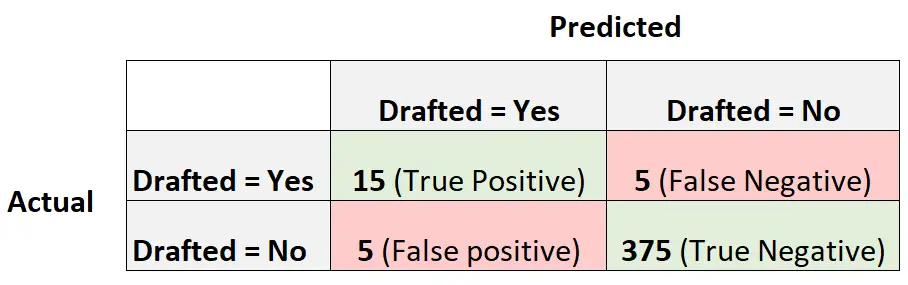
モデルのバランスの取れた精度を計算するには、まず感度と特異度を計算します。

• 感度: 「真陽性率」 = 15 / (15 + 5) = 0.75
• 特異度: 「真陰性率」 = 375 / (375 + 5) = 0.9868

次に、バランスの取れた精度を次のように計算できます。

• バランスの取れた精度 = (感度 + 特異度) / 2
• バランスの取れた精度 = (0.75 + 9868) / 2
• バランスの取れた精度 = 0.8684

モデルの平衡精度は0.8684であることがわかります。

バランスの取れた精度が 1 に近づくほど、モデルが観測値を正しく分類できるようになります。

この例では、バランスの取れた精度が非常に高く、ロジスティック回帰モデルが大学の選手が NBA にドラフトされるかどうかを非常にうまく予測していることがわかります。

このシナリオでは、クラスが非常にアンバランスであるため (20 人のプレーヤーがドラフトされ、380 人のプレーヤーがドラフトされませんでした)、バランスのとれた精度により、全体的な精度の測定と比較して、モデルのパフォーマンスのより現実的なイメージが得られます。

たとえば、モデルの精度は次のように計算します。

• 精度 = (TP + TN) / (TP + TN + FP + FN)
• 精度 = (15 + 375) / (15 + 375 + 5 + 5)
• 精度 = 0.975

モデルの精度は0.975で、非常に高いようです。

ただし、すべての選手がドラフト外になることを単純に予測するモデルを考えてみましょう。精度は 380/400 = 0.95になります。これはモデルの精度よりわずかに低いだけです。

バランスのとれた精度スコア0.8684により、両方のクラスを予測するモデルの能力がよりよくわかります。

言い換えれば、どの選手がドラフト外になるのか、どの選手がドラフト外になるのかを予測するモデルの能力をよりよく理解できるようになります。

追加リソース

次のチュートリアルでは、さまざまな統計ソフトウェアで混同行列を作成する方法を説明します。

Excel で混同行列を作成する方法
R で混同行列を作成する方法
Python で混同行列を作成する方法