パレート分布
この記事では、統計におけるパレート分布とは何か、また何に使用されるのかについて説明します。パレート分布グラフとこのタイプの確率分布のプロパティも確認できます。
パレート分布とは何ですか?
パレート分布は、パレートの法則をモデル化するために統計で使用される連続確率分布です。したがって、パレート分布は、出現確率が残りの値よりもはるかに高いいくつかの値を持つ確率分布です。
パレートの法則は 80-20 の法則とも呼ばれ、現象の原因のほとんどは人口のごく一部によるものであるという統計原則であることを思い出してください。
パレート分布には、スケール パラメーター x mと形状パラメーター α という 2 つの特徴的なパラメーターがあります。
![]()
元々、パレート分布は人口内の富の分布を表すために使用されていました。なぜなら、その大部分は人口の少数の割合によるものだったからです。しかし現在、パレート分布は、品質管理、経済学、科学、社会分野など、多くの用途に応用されています。
パレート分布は、分布を作成した経済学者のヴィルフレド パレートにちなんで名付けられました。しかし、彼はパレート図で最もよく知られています。
パレート分布表
パレート分布の定義を理解したところで、グラフで表されたパレート分布の例をいくつか見てみましょう。
したがって、以下では、パレート分布の密度関数のグラフが特性値に応じてどのように見えるかを確認できます。
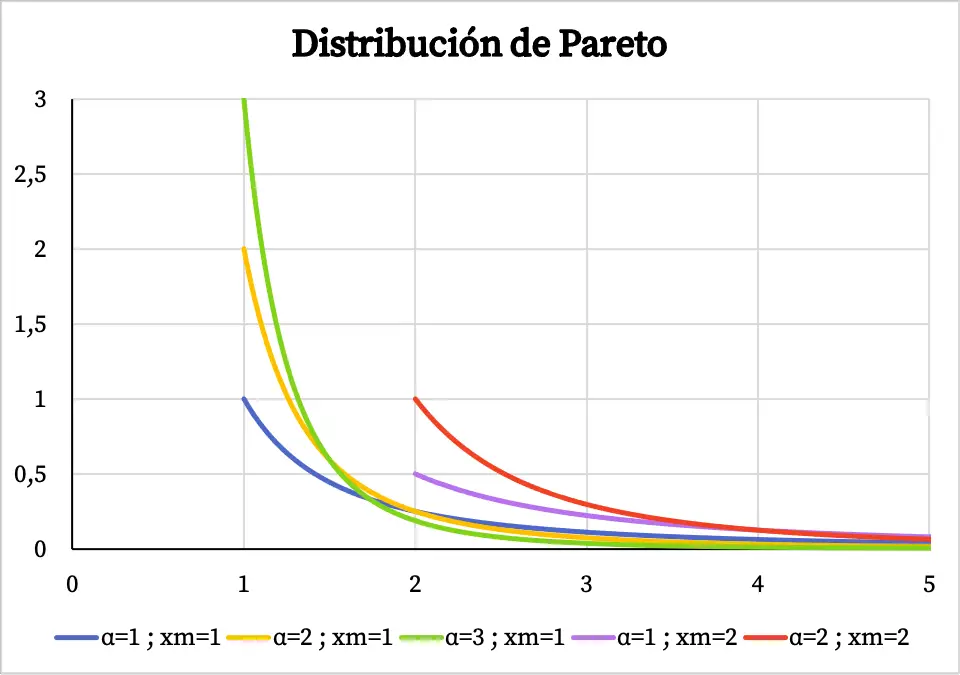
パレート分布の領域は値 x mから +∞ まで変化することに注意してください。これが、密度関数が x mの値より前に存在しない理由です。
一方、パレート分布の累積確率関数のグラフは次のようになります。
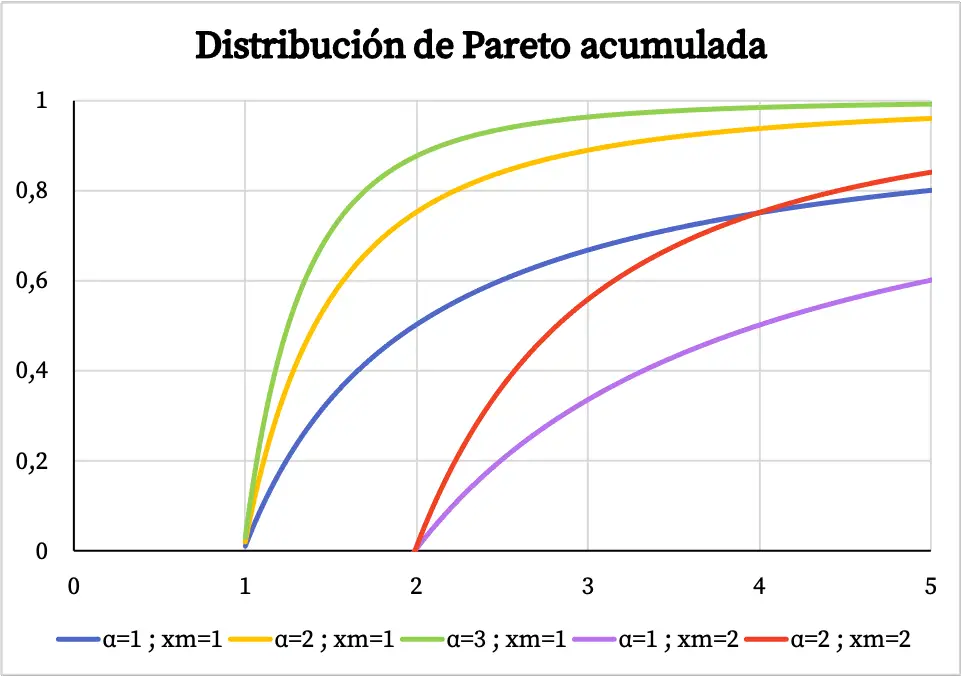
パレート分布の特徴
以下は、確率理論と統計に関連するパレート分布の最も重要な特徴です。
- パレート分布には、その曲線を定義する 2 つの特徴的なパラメーター、スケール パラメーター x mと形状パラメーター α があります。
![]()
- パレート分布の領域は、スケール パラメーターからプラス無限大までのすべての実数で構成されます。
![]()
- α が 1 より大きい場合、パレート分布の平均は、α 掛ける x mと α から 1 を引いた積に等しくなります。
![E[X]=\cfrac{\alpha\cdot x_m}{\alpha-1}\quad\text{para } \alpha>1″ title=”Rendered by QuickLaTeX.com” height=”34″ width=”214″ style=”vertical-align: -12px;”></p>
</p>
<ul>
<li>パレート分布の分散は、分布の 2 つの特性パラメータに依存し、次の式で計算されます。</li>
</ul>
<p class=](https://statorials.org/wp-content/ql-cache/quicklatex.com-6d26513868f9ed6fa45ab0fde0030884_l3.png)
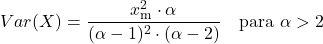
![]()
- パレート分布の最頻値は、分布のスケール パラメーター x mに相当します。
![]()
- パレート分布の密度関数の式は次のとおりです。
![]()
- 同様に、パレート分布の累積確率関数の式は次のとおりです。
![]()
- パレート分布の非対称係数は形状パラメーター α のみに依存し、その式は次のとおりです。
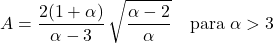
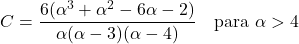
著者について
ベンジャミン・アンダーソン博士
私はベンジャミンです。退職した統計教授から、専任の Statorials 教育者になりました。 統計分野における豊富な経験と専門知識を活かして、私は Statorials を通じて学生に力を与えるために自分の知識を共有することに尽力しています。もっと知る