ピアソン相関係数

ピアソン相関係数(「積率相関係数」とも呼ばれます) は、2 つの変数XとYの間の線形関連性の尺度です。値は -1 から 1 の間です。ここで、次のとおりです。

• -1 は、2 つの変数間の完全な負の線形相関を示します。
• 0 は 2 つの変数間に線形相関がないことを示します
• 1 は、2 つの変数間の完全な正の線形相関を示します。

ピアソン相関係数を求める式

データのサンプルについて、 rで示されるピアソン相関係数を求める式は次のとおりです ( Wikipedia より)。

ソフトウェアを使用してこの式を計算できるため、おそらく手動で計算する必要はありませんが、例を確認することで、この式が正確に何を行うかを理解するのに役立ちます。

次のデータセットがあるとします。

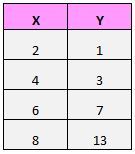
これらのペア (X、Y) を散布図にプロットすると、次のようになります。

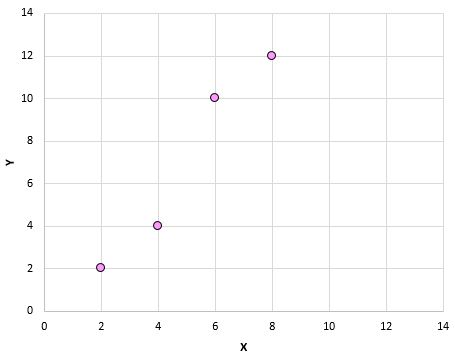
この散布図を見るだけで、変数 X と Y の間に正の相関があることがわかります。X が増加すると、Y も同様に増加する傾向があります。しかし、これら 2 つの変数がどの程度積極的に関連しているかを正確に定量化するには、ピアソン相関係数を見つける必要があります。

式の分子に注目してみましょう。

データセット内の各ペア (X、Y) について、x 値と平均 x 値の差、y 値と平均 y 値の差を見つけて、これら 2 つの数値を乗算する必要があります。

たとえば、最初のペア (X, Y) は (2, 2) です。このデータ セットの x の平均値は 5 で、このデータ セットの y の平均値は 7 です。したがって、このペアの x 値と x の平均値の差は 2 – 5 = -3 となります。このペアの y 値と平均 y 値の差は 2 – 7 = -5 です。次に、これら 2 つの数値を掛けると、-3 * -5 = 15 が得られます。

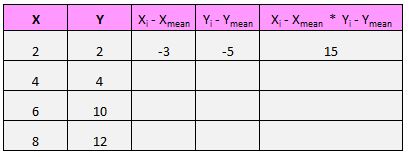
これが今行ったことの視覚的な概要です:

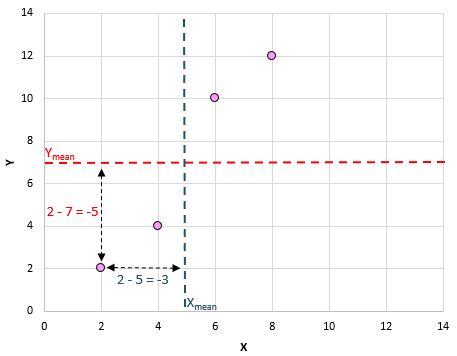
次に、各ペアに対してこれを実行します。

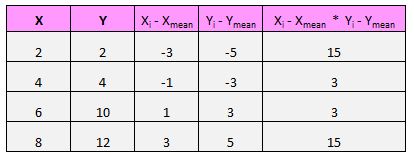
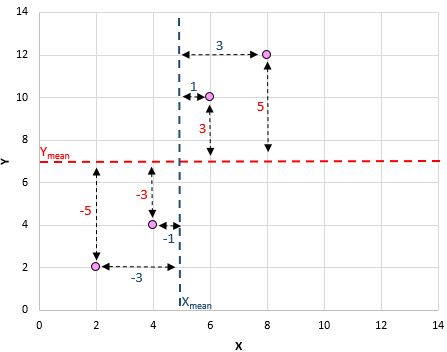
式の分子を取得する最後のステップは、これらすべての値を単純に加算することです。

15 + 3 +3 + 15 = 36

次に、式の分母は、x と y の差の二乗の合計を求め、これら 2 つの数値を掛け合わせて平方根を求めるように指示します。

したがって、まず x と y の差の二乗和を求めます。

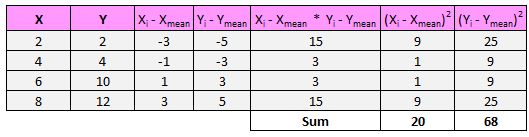
次に、これら 2 つの数値を掛け合わせます: 20 * 68 = 1,360。

最後に平方根を求めます: √ 1,360 = 36.88

したがって、式の分子は 36、分母は 36.88 であることがわかりました。これは、ピアソン相関係数が r = 36 / 36.88 = 0.976であることを意味します。

この数値は 1 に近く、変数XとYの間に強い正の線形関係があることを示しています。これは、散布図で観察された関係を裏付けています。

相関関係を表示する

ピアソン相関係数は、2 つの変数間の線形関係のタイプ(正、負、なし) と、この関係の強さ(弱い、中程度、強い) を示すことに注意してください。

2 つの変数の散布図を作成すると、2 つの変数間の実際の関係がわかります。以下に、観察される可能性のあるさまざまな種類の線形関係を示します。

強い正の関係: X 軸の変数が増加すると、Y 軸の変数も増加します。ポイントは密接に密集しており、強い関係があることを示しています。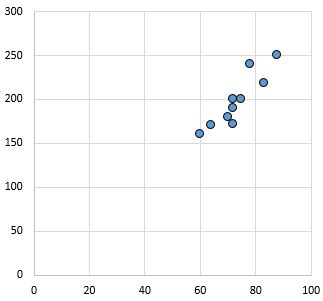

ピアソン相関係数: 0.94

弱い正の関係: X 軸の変数が増加すると、Y 軸の変数も増加します。ポイントはかなり分散しており、関係が弱いことを示しています。

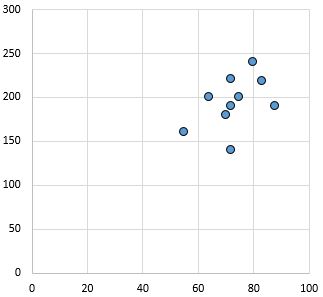
ピアソン相関係数: 0.44

関係なし:変数間に明確な関係 (正または負) がありません。

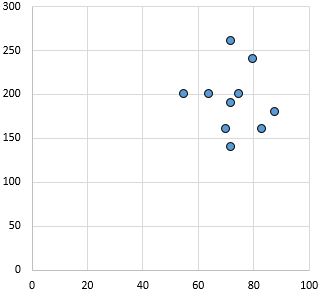
ピアソン相関係数: 0.03

強い負の関係: X 軸の変数が増加すると、Y 軸の変数は減少します。ポイントがしっかりと詰まっており、強い関係性を示しています。

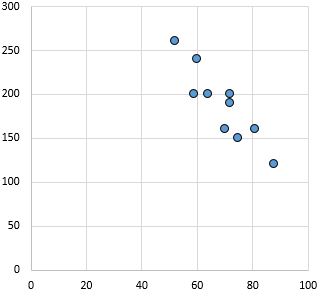
ピアソン相関係数: -0.87

弱い負の関係: X 軸の変数が増加すると、Y 軸の変数は減少します。ポイントはかなり分散しており、関係が弱いことを示しています。

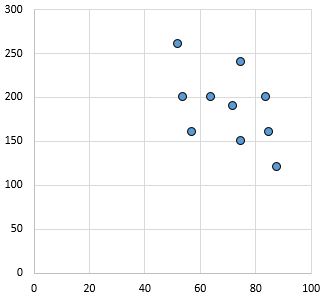
ピアソン相関係数: – 0.46

ピアソン相関係数の有意性のテスト

一連のデータのピアソン相関係数を見つけるとき、多くの場合、より大きな母集団からのデータのサンプルを使用します。これは、母集団全体で実際には相関関係がない場合でも、2 つの変数の非ゼロ相関を見つけることが可能であることを意味します。

たとえば、母集団全体のデータ ポイントごとに変数XとYの散布図を作成すると、次のようになります。

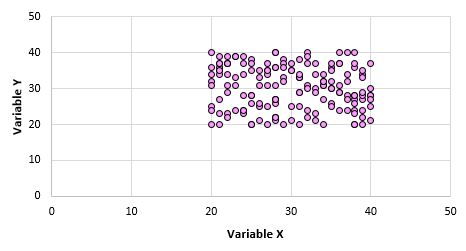
これら 2 つの変数に相関がないことは明らかです。ただし、母集団から 10 ポイントのサンプルを抽出するときに、次のポイントを選択する可能性があります。

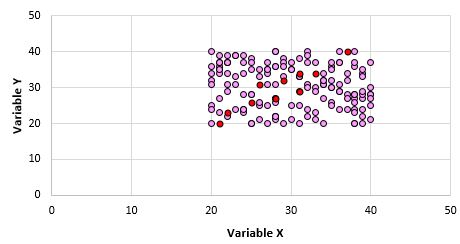
この点サンプルのピアソン相関係数は 0.93 であり、母集団相関がゼロであっても強い正の相関があることがわかります。

2 つの変数間の相関関係が統計的に有意かどうかをテストするには、次の検定統計量を見つけることができます。

検定統計量 T = r * √ (n-2) / (1-r ² )

ここで、 nはサンプル内のペアの数、 rはピアソン相関係数、T 検定統計量は n-2 自由度の分布に従います。

ピアソン相関係数の有意性を検定する方法の例を見てみましょう。

例

次のデータセットは、12 人の身長と体重を示しています。

以下の散布図は、これら 2 つの変数の値を示しています。

これら 2 つの変数のピアソン相関係数は r = 0.836 です。

検定統計量 T = 0.836 * √ (12 -2) / (1-0.836 ² ) = 4.804。

t 分布計算ツールによると、自由度 10 のスコア 4.804 の p 値は 0.0007 です。 0.0007 < 0.05 であるため、この例の体重と身長の相関は alpha = 0.05 で統計的に有意であると結論付けることができます。

予防

ピアソン相関係数は、2 つの変数に線形関連があるかどうかを知るのに役立ちますが、ピアソン相関係数を解釈する際には、次の 3 つのことに留意する必要があります。

1. 相関関係は因果関係を意味しません。 2 つの変数に相関があるからといって、一方の変数が他方の変数の出現頻度を多かれ少なかれ必然的に引き起こすわけではありません。この典型的な例は、アイスクリームの売上とサメの攻撃との間の正の相関関係です。一年の特定の時期にアイスクリームの売り上げが増加すると、サメによる襲撃も増加する傾向があります。

ということは、アイスクリームを食べるとサメに襲われるということなのでしょうか？もちろん違います！これは単純に、夏には氷の人気が高まり、海に入る人が増えるため、夏には氷の消費とサメの攻撃が増加する傾向があることを意味します。

2. 相関関係は外れ値の影響を受けやすくなります。極端な外れ値はピアソン相関係数を大きく変える可能性があります。以下の例を考えてみましょう。

変数XとYのピアソン相関係数は0.00です。しかし、データセットに外れ値があると想像してください。

ただし、これら 2 つの変数のピアソン相関係数は0.878です。この 1 つの異常値がすべてを変えます。このため、2 つの変数の相関関係を計算するときは、散布図を使用して変数を視覚化し、外れ値をチェックすることをお勧めします。

3. ピアソン相関係数は、2 つの変数間の非線形関係を捉えません。次の関係を持つ 2 つの変数があると想像してみましょう。

これら 2 つの変数のピアソン相関係数は、線形関係がないため 0.00 です。ただし、これら 2 つの変数には非線形の関係があります。y 値は単に x 値を二乗したものです。

ピアソン相関係数を使用する場合は、2 つの変数が線形に関連しているかどうかをテストしているだけであることに留意してください。たとえピアソン相関係数によって 2 つの変数に相関がないことが示されたとしても、それらには依然として何らかの非線形関係がある可能性があります。これが、2 つの変数間の関係を分析するときに散布図を作成することが役立つもう 1 つの理由です。非線形関係を検出するのに役立ちます。