Stata で breusch-pagan テストを実行する方法
重線形回帰は、複数の説明変数と応答変数の間の関係を理解するために使用できる方法です。
残念ながら、回帰でよく発生する問題は不均一分散として知られており、測定値の範囲にわたって残差の分散に系統的な変化が生じます。
不均一分散性が存在するかどうかを判断するために使用できるテストの 1 つは、 Breusch-Pagan テストです。この検定では、カイ二乗検定統計量と対応する p 値が生成されます。
p 値が特定のしきい値 (一般的な選択肢は 0.01、0.05、および 0.10) を下回っている場合、不均一分散性が存在すると言える十分な証拠があります。
このチュートリアルでは、Stata で Breusch-Pagan テストを実行する方法を説明します。
例: Stata での Breusch-Pagan テスト
自動的に統合された Stata データセットを使用して、Breusch-Pagan テストの実行方法を説明します。
ステップ 1: データをロードして表示します。
まず、次のコマンドを使用してデータをロードします。
システムの自動使用
次に、次のコマンドを使用して生データを表示します。
br
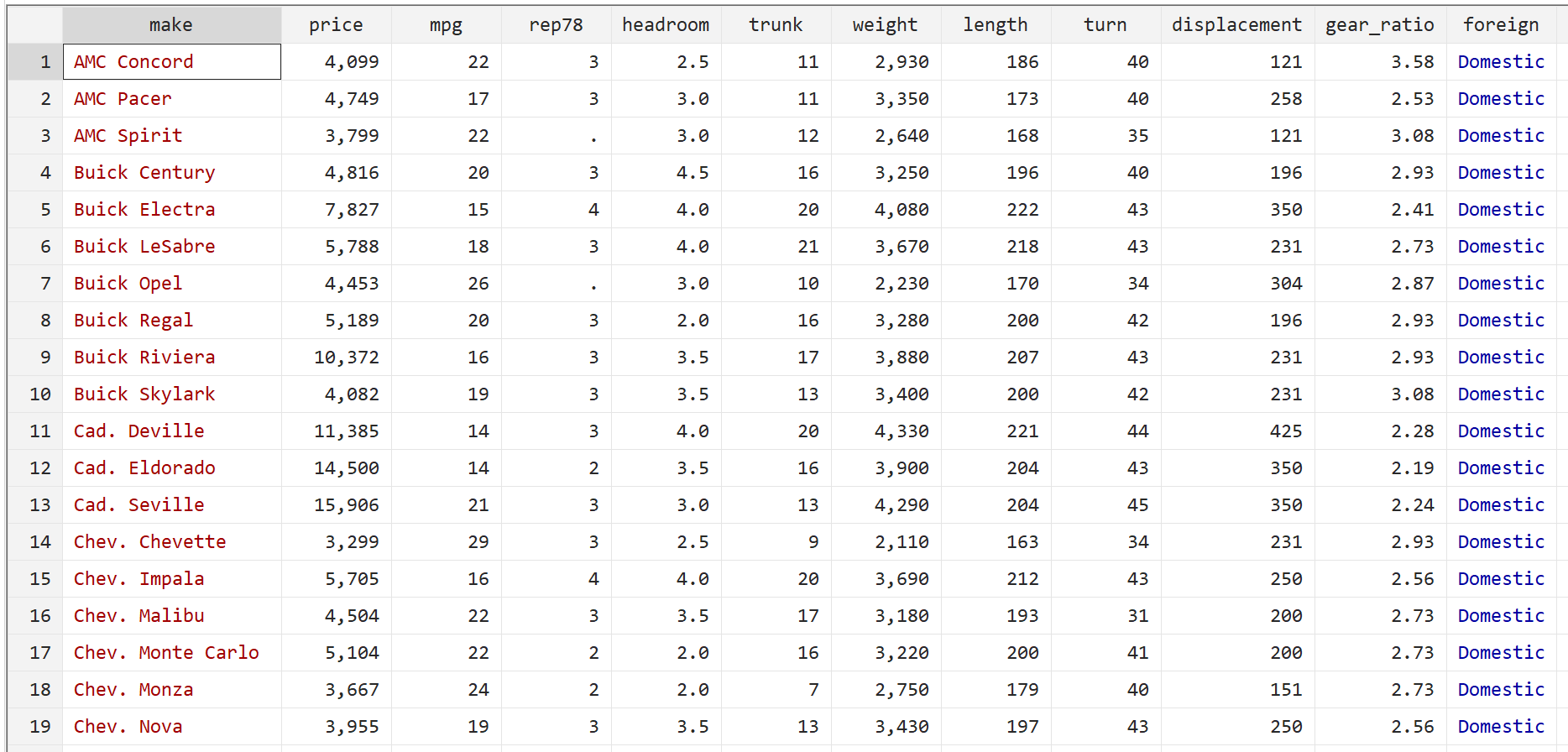
ステップ 2: 重回帰を実行します。
次に、次のコマンドを入力して、応答変数として価格、説明変数としてmpgとweightを使用して重線形回帰を実行します。
回帰価格 mpg 重量

ステップ 3: ブリューシュ・パガン テストを実行します。
回帰モデルを当てはめたら、 hettestコマンドを使用して Breusch-Pagan テストを実行できます。これは「不均一分散性テスト」の略です。
一番ホットな

結果を解釈する方法は次のとおりです。
Ho:これは検定の帰無仮説であり、残差間に一定の分散があることを示します。
変数:これにより、回帰モデルで使用された応答変数がわかります。この場合、それは変動価格でした。
chi2(1):これは検定のカイ二乗検定統計量です。この場合、午後 2 時 78 分です。
Prob > chi2:これは、カイ二乗検定統計量に対応する p 値です。この場合は 0.0001 です。この値が 0.05 未満であるため、帰無仮説は棄却され、データには不均一分散があると結論付けることができます。
次はどうする
Breusch-Pagan 検定の帰無仮説を棄却できなかった場合、不均一分散性は存在しないため、元の回帰の結果の解釈に進むことができます。
ただし、Breusch-Pagan 検定の帰無仮説を棄却すると、データに不均一分散性が存在することになります。この場合、回帰出力テーブルに表示される標準誤差は信頼できません。この問題を解決するには、次のようないくつかの方法があります。
1. 応答変数を変換します。応答変数に対して変換を実行してみることができます。たとえば、応答変数として、price の代わりに log(price) を使用できます。一般に、応答変数の対数を取得することは、不均一分散性を排除する効果的な方法です。もう 1 つの一般的な変換は、応答変数の平方根を使用することです。
2. 重み付け回帰を使用します。このタイプの回帰では、近似値の分散に基づいて各データ ポイントに重みが割り当てられます。基本的に、これにより、分散が大きいデータ ポイントに低い重みが与えられ、残差二乗が減少します。適切な重みを使用すると、不均一分散性の問題を解決できます。
3. 堅牢な標準誤差を使用します。ロバストな標準誤差は、不均一分散性の問題に対してより「ロバスト」であり、回帰係数の真の標準誤差のより正確な測定値を提供する傾向があります。 Stata の回帰で堅牢な標準誤差を使用する方法については、このチュートリアルをご覧ください。