フィット感の質
この記事では、統計における適合度について説明します。同様に、回帰モデルの適合度を測定する方法を示し、さらに、適合度の解決済みの演習を確認することができます。
フィット感の良さとは何でしょうか?
統計学における適合度は、回帰モデルがデータ サンプルにどの程度適合するかを表します。言い換えれば、回帰モデルの適合度は、一連の観測値と回帰によって得られた値との間の結合のレベルを指します。
したがって、回帰モデルの適合度が高いほど、調査対象のデータをよりよく説明できます。したがって、統計モデルの適合性が高いほど、より良い結果が得られます。
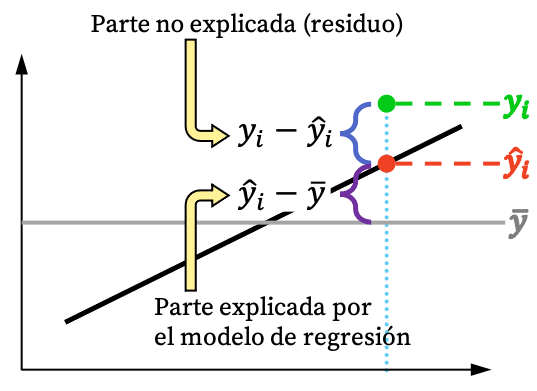
上の画像からわかるように、観測値は通常、回帰モデルでは完全に説明できません。しかし論理的には、回帰モデルがデータセットからより多くのことを説明できるほど、モデルはより適切に適合します。つまり、できる限り厳密な回帰モデルに興味があるのです。
回帰モデルの適合度
回帰モデルの適合度を判断するには、通常、回帰モデルによって説明されるパーセンテージを示す統計係数である決定係数を使用します。したがって、モデルの決定係数が高いほど、モデルはデータ サンプルに適切に適合します。
![]()
ただし、回帰モデルの変数が多いほど、決定係数が高くなることに注意してください。このため、調整された決定係数は、モデルの適合度を測定するためにもよく使用されます。調整された決定係数は、回帰モデルによって説明されるパーセンテージを示す前の係数の変化であり、モデルに含まれる各説明変数にペナルティを与えます。
![]()
したがって、モデルに含まれる変数の数が考慮されるため、調整された決定係数を使用して、多数の異なる変数を含む 2 つのモデルを比較することが好ましい。
最後に、通常は前の 2 つの係数の値が使用されますが、カイ二乗検定は回帰モデルの適合度を測定するためにも使用できることに注意してください。
適合性の具体例
最後に、この統計的概念の吸収を完了するために、調整の質に関する解決済みの演習を見ていきます。
- 同じデータ系列を使用して 2 つの異なる線形回帰モデルが実行され、その結果が次の表に示されています。どのモデルを使用するのが最適ですか?
| 回帰モデル 1 | 回帰モデル 2 | |
|---|---|---|
| 決定係数 | 57% | 64% |
| 調整後の決定係数 | 49% | 43% |
| 説明変数の数 | 3 | 7 |
この場合、両方のモデルが線形回帰モデルの以前の仮定を満たしていると仮定するため、モデルの適合度を分析するだけで済みます。
回帰モデル 2 は回帰モデル 1 よりも決定係数が高く、データ サンプルをより適切に説明できるため、アプリオリに優れた回帰モデルであると考えられます。
ただし、回帰モデル 2 にはモデル内に 7 つの独立変数がありますが、回帰モデル 1 には 3 つしかありません。そのため、モデル 2 は最初のモデルよりもはるかに複雑で、解釈が難しくなります。
さらに、モデル内の変数の数を考慮した調整後の決定係数を見ると、回帰モデル 1 の方が回帰モデル 2 よりも高い調整後の決定係数を持っています。
結論として、回帰モデル 1 を使用する方が良いですが、調整後の決定係数は回帰モデル 2 よりも高いためです。回帰モデル 2 の未調整の決定係数はより高くなりますが、これは回帰モデルにより多くの変数が含まれているためです。モデル 1. モデル。この係数の値は増加しますが、モデルの解釈がより困難になり、確実に新しい値の予測が悪化します。
変数の数が異なるモデルを比較するには、モデルに追加された各変数にペナルティが課されるため、調整された決定係数を使用することが最善です。この例で見たように、調整されていない決定係数によれば、回帰モデル 2 の方が優れていますが、調整された決定係数を通じて、実際には回帰モデル 1 の方が優れていることがわかります。