ベータ版の配布

この記事では、ベータ版配布とは何か、またその用途について説明します。同様に、ベータ分布グラフとこのタイプの確率分布のプロパティを確認できます。

ベータ版の配布とは何ですか?

ベータ分布は、区間 (0,1) で定義され、2 つの正のパラメーター α と β によってパラメーター化された確率分布です。つまり、ベータ分布の値はパラメータαとβに依存します。

したがって、ベータ分布の主な特徴は、その形状がパラメータ α と β によって制御できることです。さらに、ベータ分布は、値が 0 から 1 までの確率変数を定義するために使用されます。

連続確率変数がベータ分布によって支配されることを示す表記法がいくつかありますが、最も一般的なものは次のとおりです。

統計では、ベータ分布は非常に多様な用途に使用されます。たとえば、ベータ分布は、さまざまなサンプルのパーセンテージの変動を調べるために使用されます。同様に、プロジェクト管理では、Pert 分析を実行するためにベータ配布が使用されます。

ベータ分布プロット

ベータ分布の定義を考慮して、ベータ分布の密度関数と確率分布関数を以下にプロットします。

以下に、ベータ分布の密度関数グラフがパラメーター α と β に応じてどのように変化するかを示します。

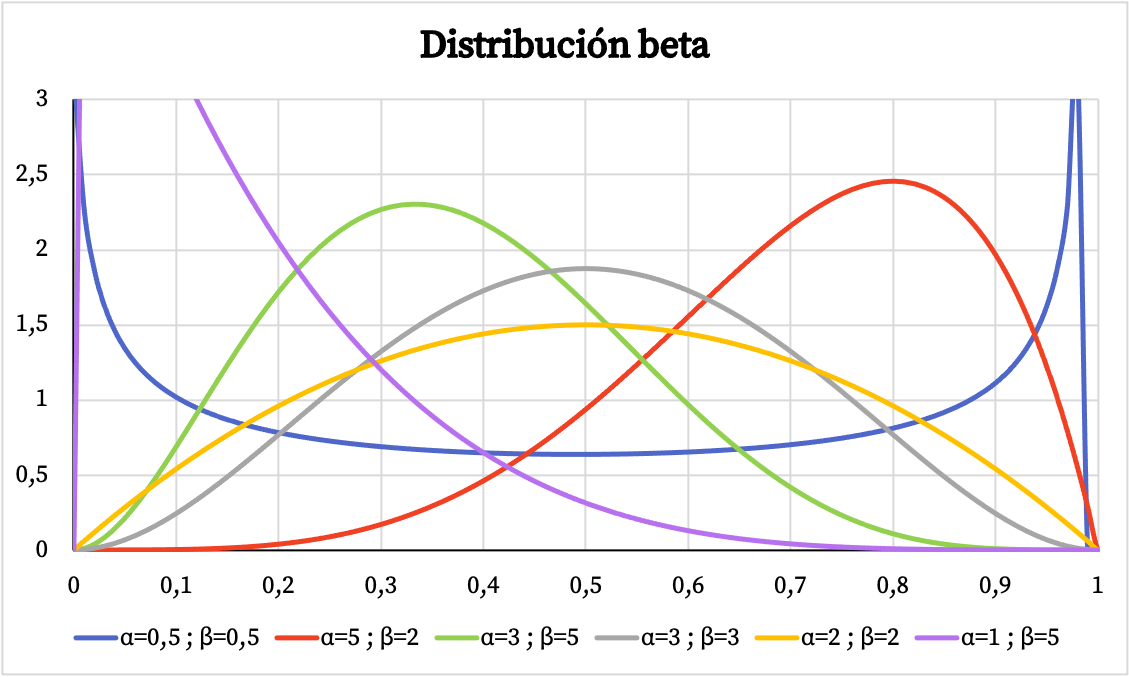
同様に、以下では、パラメーター α と β に基づくベータ分布の累積確率のグラフ表示を確認できます。

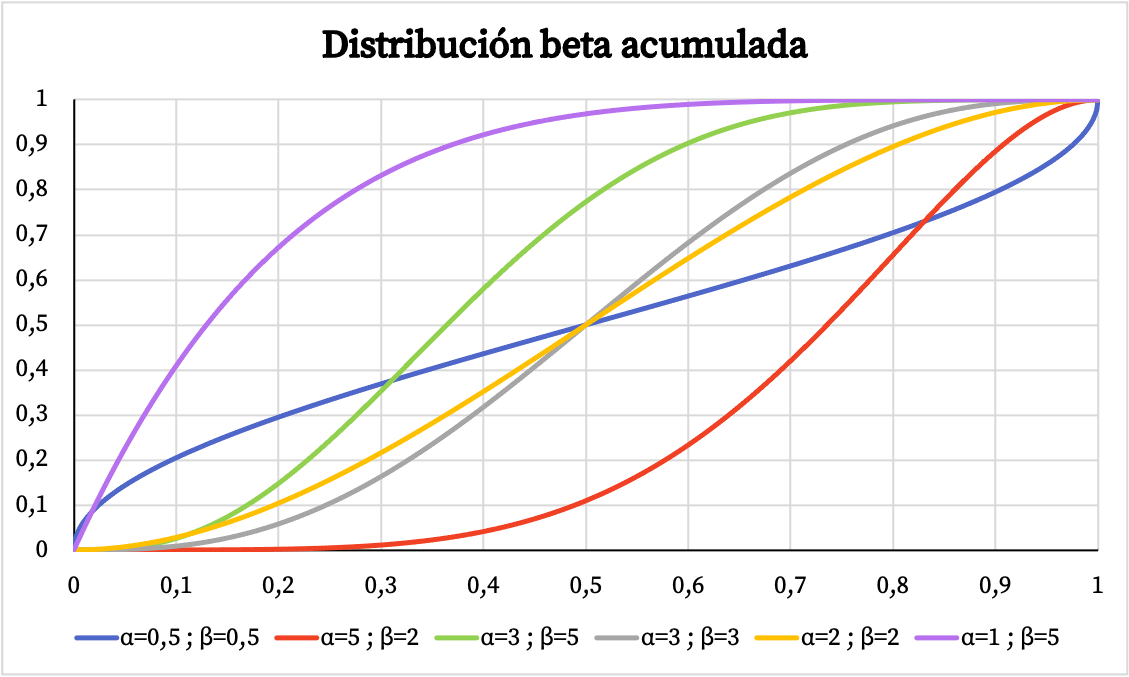
ベータ版ディストリビューションの特徴

このセクションでは、ベータ版ディストリビューションの最も重要な特徴が何かを見ていきます。

• ベータ分布のパラメータ α と β は、実数の正の数です。

• ベータ分布の平均は、アルファをアルファとベータの合計で割ったものに等しくなります。

• ベータ分布の分散は、次の式を使用して計算できます。

• アルファとベータの値が 1 より大きい場合、ベータ分布モードは次の式で簡単に見つけることができます。

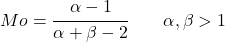
ここで、B(α,β) はベータ関数であり、次のように定義されます。

• ベータ分布の累積確率関数は次のとおりです。

ここで、B(x;α,β) は不完全ベータ関数であり、次のように定義されます。

• X がベータ分布によって定義される変数の場合、1-X はベータ分布によって定義される変数であり、そのアルファ パラメーターとベータ パラメーターはそれぞれ元のベータ分布のベータ パラメーターとアルファ パラメーターになります。

• ベータ分布のアルファ パラメータとベータ パラメータが両方とも 1 に等しい場合、その分布はパラメータ 0 と 1 の一様分布と等価です。