Spss で manova を実行する方法
一元配置分散分析は、説明変数の異なる水準が特定の応答変数において統計的に異なる結果をもたらすかどうかを判断するために使用されます。
たとえば、3 つの教育レベル (準学士号、学士号、修士号) が統計的に異なる年収につながるかどうかを理解することに興味があるかもしれません。この場合、説明変数と応答変数があります。
- 説明変数:教育レベル
- 応答変数:年収
MANOVA は、複数の応答変数がある一元配置分散分析を拡張したものです。たとえば、教育レベルによって年収や学生ローンの額が異なるかどうかを理解することに興味があるかもしれません。この場合、1 つの説明変数と 2 つの応答変数があります。
- 説明変数:教育レベル
- 応答変数:年収、学生ローン
複数の応答変数があるため、この場合は MANOVA を使用するのが適切です。
このチュートリアルでは、SPSS で MANOVA を実行する方法を説明します。
例: SPSS の MANOVA
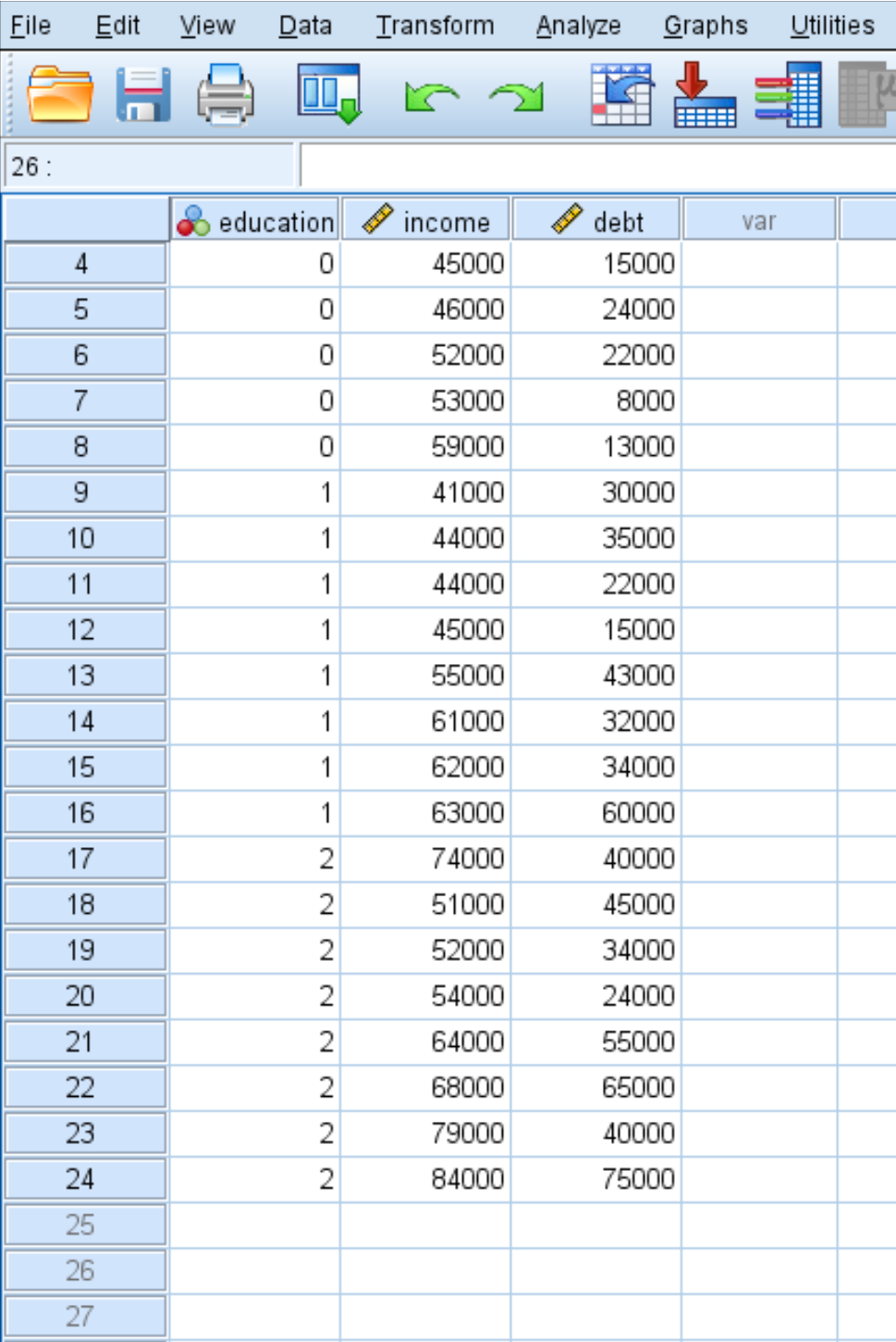
SPSS で MANOVA を実行する方法を説明するために、24 人に対する次の 3 つの変数を含む次のデータ セットを使用します。
- educ:学習レベル (0 = アソシエイト、1 = 学士、2 = 修士)
- 収入:年収
- 負債:学生ローンの負債総額
SPSS で MANOVA を実行するには、次の手順を使用します。
ステップ 1: MANOVA を実行します。
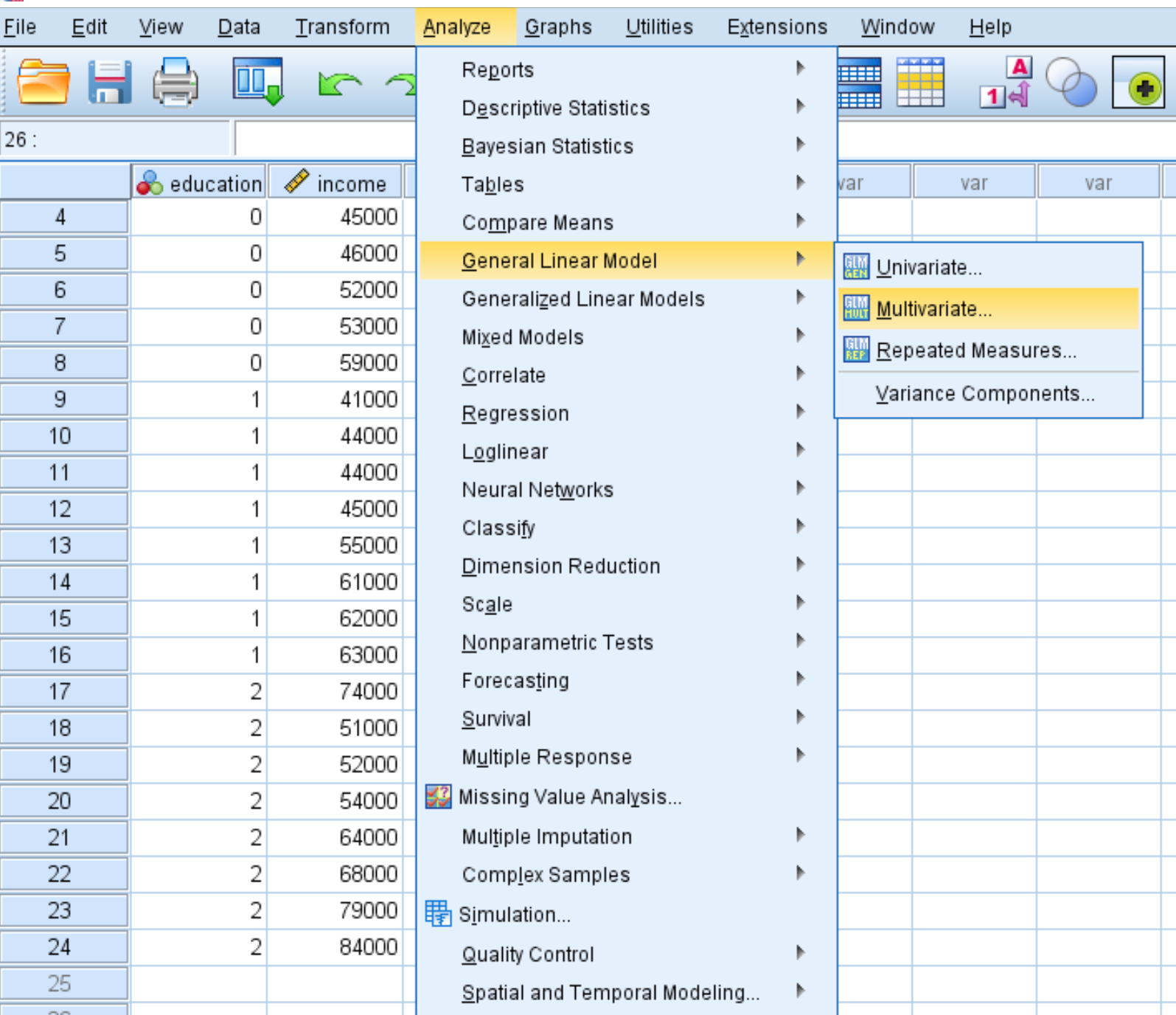
[分析]タブ、 [一般線形モデル] 、 [多変量]の順にクリックします。
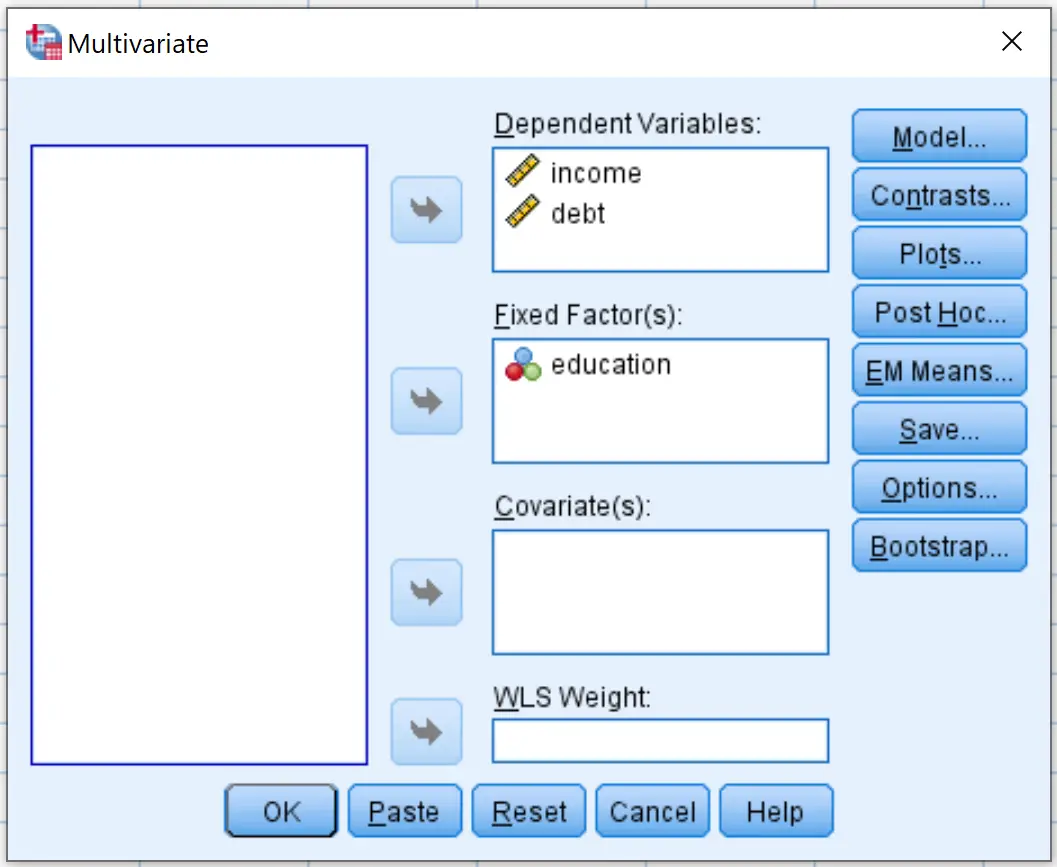
表示される新しいウィンドウで、収入変数と借金変数を「従属変数」というラベルのボックスにドラッグします。次に、教育因子変数を「固定因子」というラベルのボックスにドラッグします。
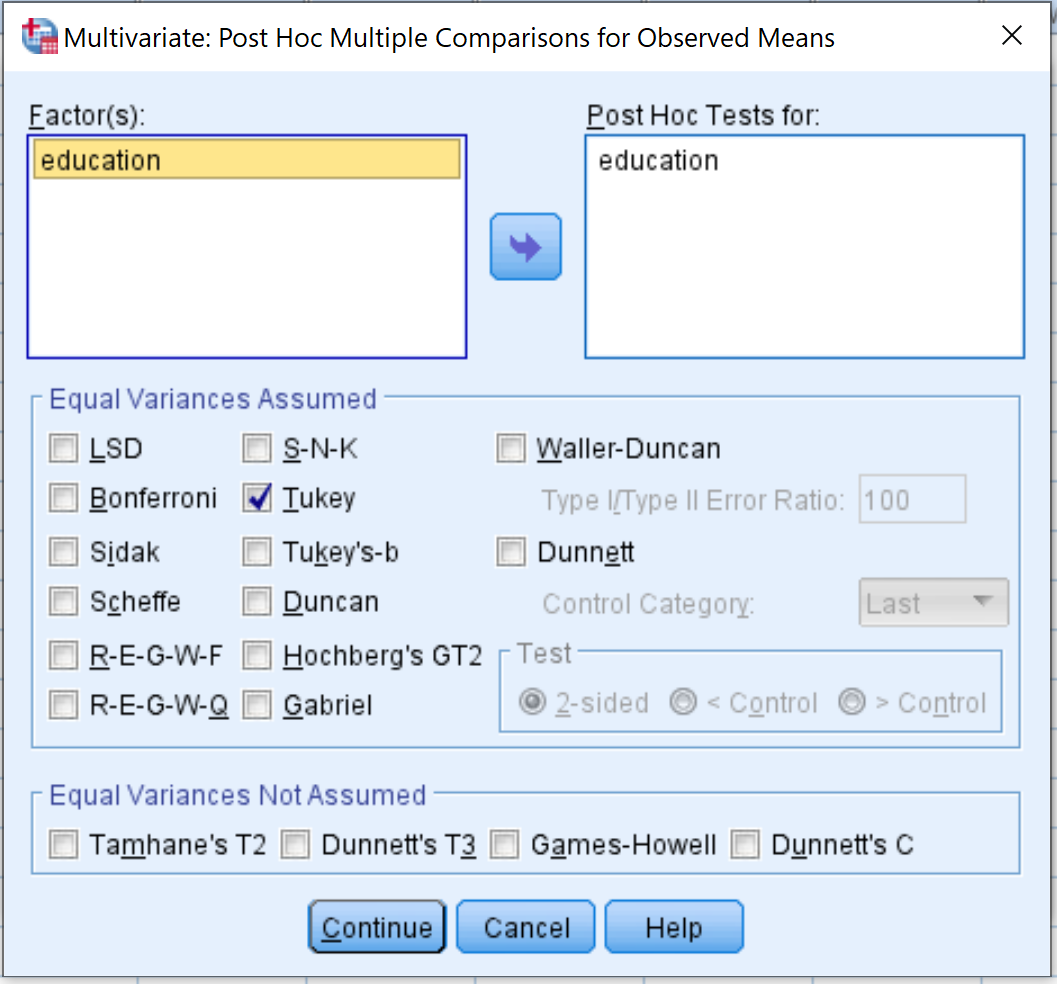
次に、 「ポストホック」ボタンをクリックします。教育係数を「Post-Hoc Tests for 」というラベルのボックスにドラッグします。次に、 Tukeyの横にあるボックスをオンにします。次に、 「続行」をクリックします。
最後に、 「OK」をクリックします。
ステップ 2: 結果を解釈します。
[OK]をクリックすると、MANOVA の結果が表示されます。結果を解釈する方法は次のとおりです。
多変量テスト
この表は、学歴によって年収と学生負債総額に統計的に有意な差が生じるかどうかを示しています。 Wilks のラムダというラベルの付いた行の数値を見てみましょう。
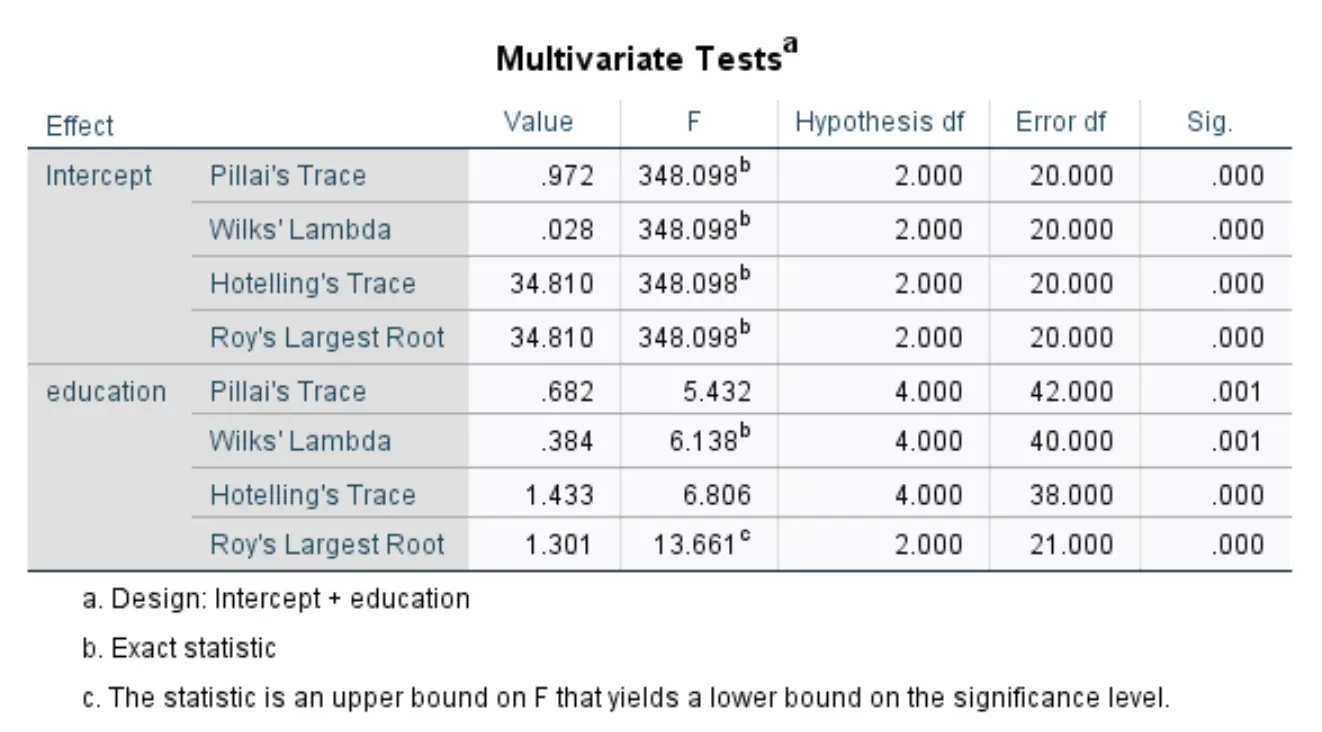
全体的な F 統計量は6.138で、対応する p 値は0.001です。この値は 0.05 未満であるため、教育レベルが年収と学生負債総額に大きな影響を与えていることがわかります。
被験者間の効果のテスト
この表は、収入と負債の個別の p 値を示しています。
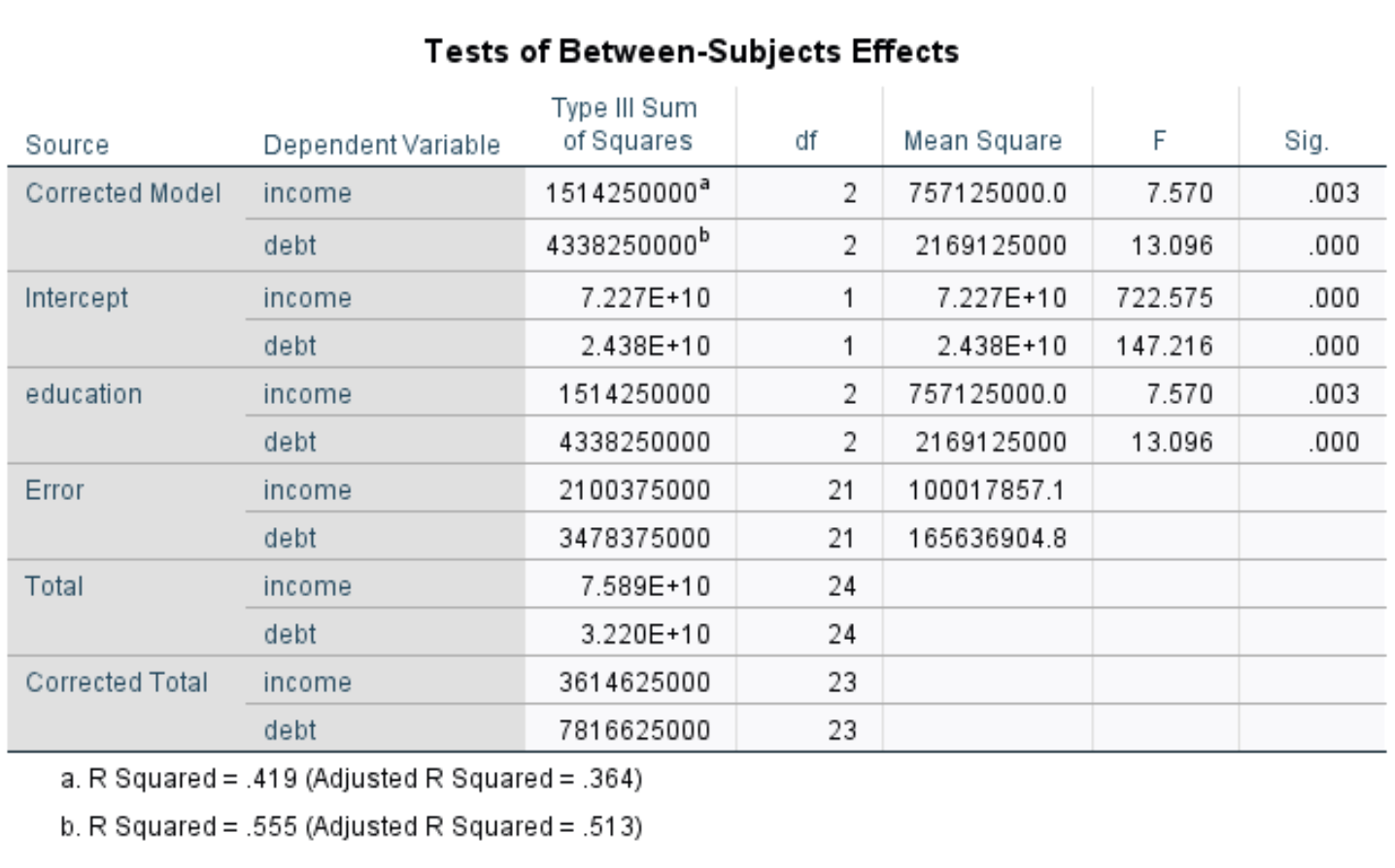
収入の p 値は0.003 、負債の p 値は0.000です。これら 2 つの値は 0.05 未満であるため、これは教育レベルが収入と負債に統計的に有意な影響を与えていることを意味します。
事後テスト
この表は、教育レベルごとの Tukey の事後比較を示しています。
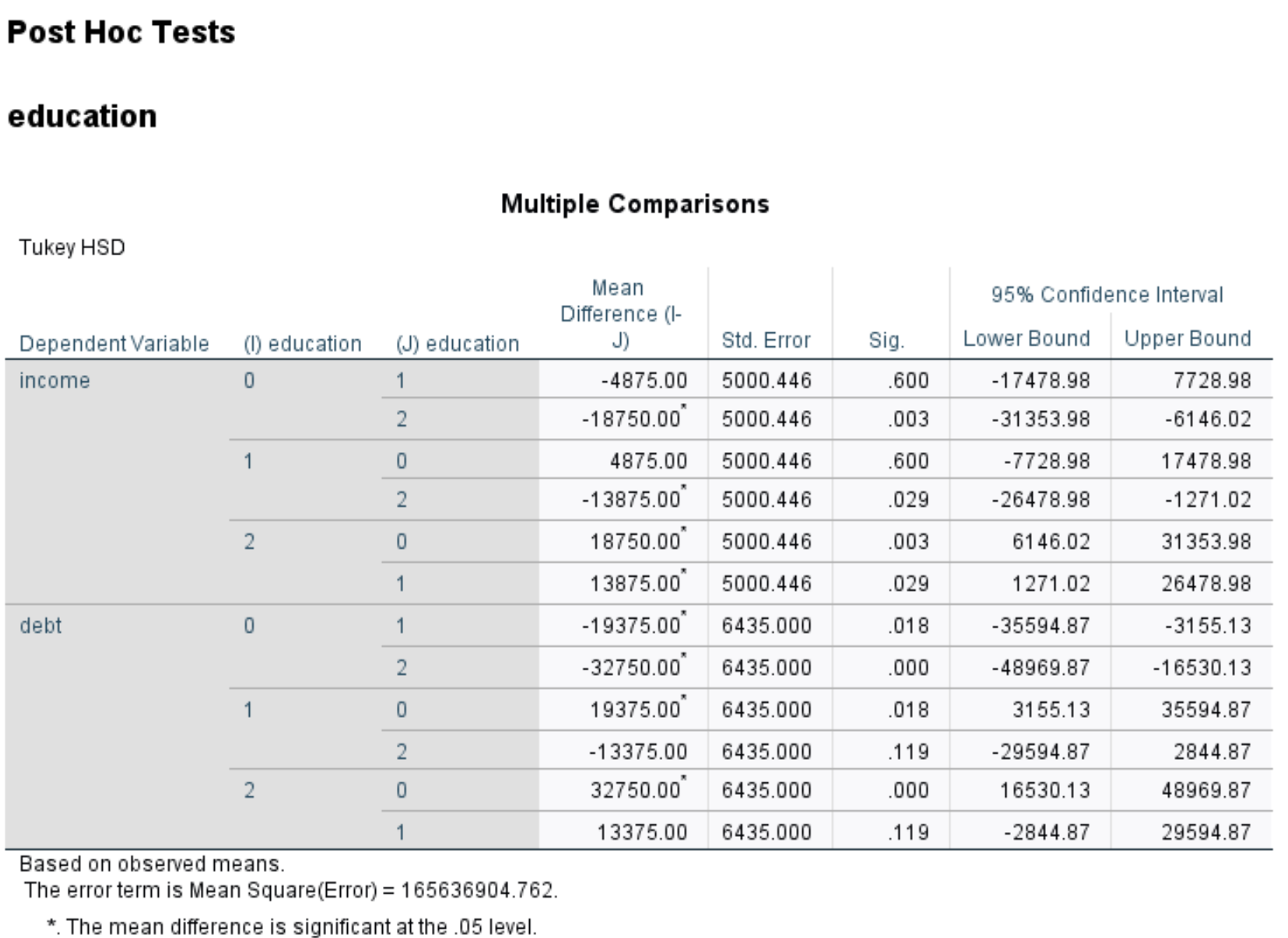
表から次のことがわかります。
- 準学士号取得者 (学歴 = 0) の収入額は、修士号取得者 (学歴 = 1) の収入額と大きく異なります。 p 値 = 0.003 。
- 学士号 (学歴 = 1) の人の収入額は、修士号 (学歴 = 2) の人の収入額と大きく異なります。 p 値 = 0.029 。
- 準学士号 (学歴 = 0) の人の収入額は、学士号 (学歴 = 1) の人の収入額と大きく異なります。 p 値 = 0.018 。
- 準学士号 (学歴 = 0) の人の収入額は、修士号 (学歴 = 2) の人の収入額と大きく異なります。 p 値 = 0.000 。