R で mann-kendall トレンド テストを実行する方法
Mann-Kendall トレンド テストは、時系列データにトレンドがあるかどうかを判断するために使用されます。これはノンパラメトリック検定であり、データの正規性について基礎的な仮定が行われていないことを意味します。
テスト仮説は次のとおりです。
H 0 (帰無仮説):データに傾向は存在しません。
H A (対立仮説):データには傾向が存在します。 (これは良い傾向または悪い傾向である可能性があります)
検定の p 値が特定の有意レベル (一般的な選択肢は 0.10、0.05、および 0.01) を下回っている場合、時系列データに傾向が存在するという統計的に有意な証拠があります。
このチュートリアルでは、R で Mann-Kendall トレンド テストを実行する方法について説明します。
例: R での Mann-Kendall 傾向検定
R で Mann-Kendall トレンド テストを実行するには、 KendallライブラリのMannKendall()関数を使用します。この関数は次の構文を使用します。
マンケンダル(x)
金:
- x = データのベクトル、多くの場合時系列
テストの実行方法を説明するために、 Kendall Library の組み込みPrecipGLデータセットを使用します。このデータセットには、1900 年から 1986 年までのすべての五大湖の年間降水量情報が含まれています。
#load Kendall library and PrecipGL dataset library(Kendall) data(PrecipGL) #view dataset PrecipGL Time Series: Start = 1900 End = 1986 Frequency = 1 [1] 31.69 29.77 31.70 33.06 31.31 32.72 31.18 29.90 29.17 31.48 28.11 32.61 [13] 31.31 30.96 28.40 30.68 33.67 28.65 30.62 30.21 28.79 30.92 30.92 28.13 [25] 30.51 27.63 34.80 32.10 33.86 32.33 25.69 30.60 32.85 30.31 27.71 30.34 [37] 29.14 33.41 33.51 29.90 32.69 32.34 35.01 33.05 31.15 36.36 29.83 33.70 [49] 29.81 32.41 35.90 37.45 30.39 31.15 35.75 31.14 30.06 32.40 28.44 36.38 [61] 31.73 31.27 28.51 26.01 31.27 35.57 30.85 33.35 35.82 31.78 34.25 31.43 [73] 35.97 33.87 28.94 34.62 31.06 38.84 32.25 35.86 32.93 32.69 34.39 33.97 [85] 32.15 40.16 36.32 attr(,"title") [1] Annual precipitation, 1900-1986, Entire Great Lakes
データに傾向があるかどうかを確認するには、Mann-Kendall 傾向検定を実行します。
#Perform the Mann-Kendall Trend Test
MannKendall(PrecipGL)
tau = 0.265, 2-sided pvalue = 0.00029206
検定統計量は0.265で、対応する両側 p 値は0.00029206です。この p 値は 0.05 未満であるため、検定の帰無仮説を棄却し、データに傾向が存在すると結論付けます。
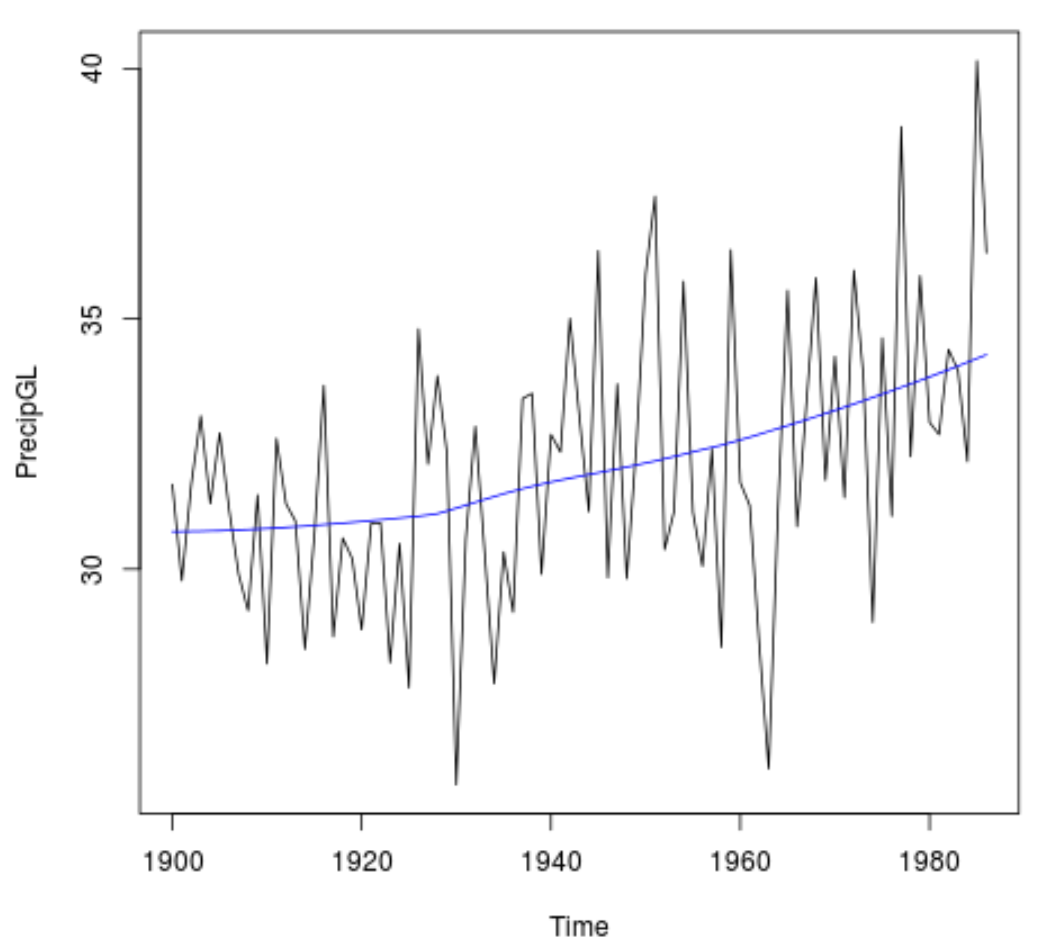
傾向を視覚化するには、年間降水量の時間プロットを作成し、傾向を表す滑らかな線を追加します。
#Plot the time series data plot(PrecipGL) #Add a smooth line to visualize the trend lines(lowess(time(PrecipGL),PrecipGL), col='blue')
SeasonalMannKendall(x)コマンドを使用して、データの季節性を考慮して、季節調整された Mann-Kendall トレンド テストを実行することもできることに注意してください。
#Perform a seasonally-adjusted Mann-Kendall Trend Test
SeasonalMannKendall(PrecipGL)
tau = 0.265, 2-sided pvalue = 0.00028797
検定統計量は0.265で、対応する両側 p 値は0.00028797です。この場合も、この p 値は 0.05 未満であるため、検定の帰無仮説を棄却し、データに傾向が存在すると結論付けます。