二乗平均平方根

によるベンジャミン・アンダーソン博士 8月 6, 2023 統計 0コメント

ここでは二乗平均平方根とは何か、またその計算方法について説明します。さらに、平均値を使用する利点と欠点、および段階的に解決された演習を学びます。最後に、記事の最後にある計算ツールを使用して、任意のデータセットの二乗平均平方根を計算できるようになります。

平均二乗とは何ですか?

二乗平均平方根は、記述統計の中心性の尺度です。二乗平均平方根は、データの二乗の算術平均の平方根に等しい。

二乗平均平方根は、二乗平均平方根またはRMSとも呼ばれます。

したがって、二次平均の公式は次のようになります。

二乗平均は、各データを二乗するとすべての値が正になるため、統計変数が正と負の値をとる場合に特に便利です。したがって、二乗平均は、符号が重要ではなく、その絶対値が重要である変数を分析するために使用されます。

たとえば、二乗平均は測定誤差を調べるために使用されます。この場合、誤差が正か負かではなく、測定時の誤差の大きさを分析するためです。

さらに、大きな数字の平方は小さな数字の平方よりもはるかに高い値を持つため、中央の正方形では小さな数字よりも大きな数字の方が重要です。

二乗平均は、算術平均、加重平均、幾何平均、調和平均と並ぶ統計平均の一種です。

二次平均には、他のタイプの平均と比較して長所と短所があります。

二次平均の主な利点は、離散変数の平均値の非常に良好な近似値を取得できることです。一方、二乗平均の大きな欠点は、いくつかの演算を実行する必要があるため、計算が非常に複雑であることです。

対照的に、二乗平均平方根は誤差測定の分析に非常に役立ちます。また、高い値がより重要になりますが、この特性は、間違った測定によって rms 結果が大幅に変化することを意味します。

二乗平均平方根を計算するには、次の手順を実行する必要があります。

👉以下の計算機を使用して、任意のデータセットの二乗平均平方根を計算できます。

二乗平均平方根を取得する方法がわかったら、例としてデータセットの二乗平均平方根を決定します。

大学の実験室の授業で、教授は学生に化学物質を使った実験をするように頼みます。化学実験の目標は、合計 3 リットルの溶液を得ることです。学生グループは次のデータを取得しました。

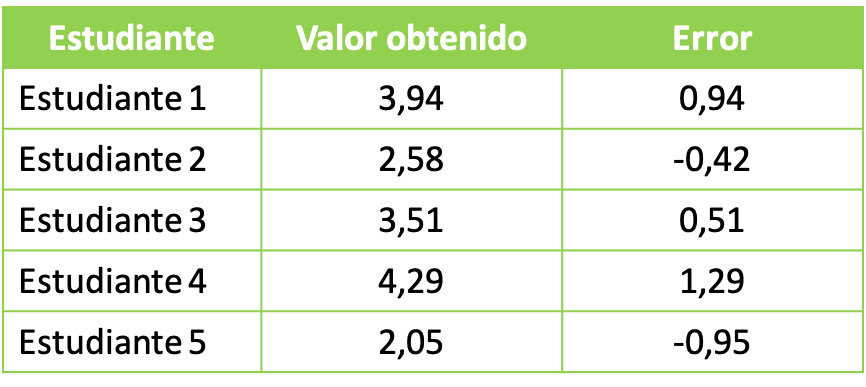
得られた統計データを調べるために、各グループから得られた誤差を含む二乗平均の値を計算します。したがって、二次平均の公式を適用します。

$\displaystyle RMS=\displaystyle\sqrt{\frac{1}{N}\sum_{i=1}^N x_i^2}=\sqrt{\frac{x_1^2+x_2^2+\dots + x_N^2}{N}\vphantom{\sum_{i=1}^N x_i^2}}}$

そして、データを式に代入して二乗平均平方根を計算します。

$\displaystyle RMS=\sqrt{\frac{0,94^2+(-0,42)^2+0,51^2+1,29^2+(-0,95)^2}{5}}=0,88$

したがって、二乗平均平方根による実験で得られた平均誤差は 0.88 リットルになります。

統計サンプルのデータを次の計算機に入力して、二乗平均平方根を計算します。データはスペースで区切られ、小数点としてピリオドを使用して入力する必要があります。

私はベンジャミンです。退職した統計教授から、専任の Statorials 教育者になりました。統計分野における豊富な経験と専門知識を活かして、私は Statorials を通じて学生に力を与えるために自分の知識を共有することに尽力しています。もっと知る