モンティ・ホール問題: 簡単な視覚的説明

Let’s Make a Dealという古いゲーム番組で、司会者のモンティ ホールは出場者に 3 つのドアをプレゼントしました。

ドアの 1 つは賞品が入っていましたが、他の 2 つは入っていませんでした。

モンティは出場者に、どのドアに賞品が入っていると思うかを選択するよう求めました。

出場者がドアを選択すると、モンティは賞品の入っていないドアを開けます。

賞品は 2 つの密室のうちの 1 つに保管されていました。

次に、モンティは候補者にドアを変更したいかどうか尋ねます。

信じられないかもしれませんが、ゲームのこの時点でドアを変更すると、実際に勝つチャンスが大きくなることがわかります。

その理由を知るために読み続けてください。

モンティ・ホール問題を視覚的に説明する

ドアを変更すると勝つ確率が高くなる理由を説明するために、最初にドア 1 を選択する次のシナリオを考えてみましょう。

シナリオ 1: ドア 1 を選択すると、賞品は実際にはドア 1 の後ろにあります。

この場合、モンティはドア 2 または 3 を開け、どちらのドアの後ろにも何もないことを示します。ドア 1 に留まれば勝ちです。

シナリオ 2: ドア 1 を選択すると、賞品は実際にはドア 2 の後ろにあります。

この場合、モンティはドア 3 を開け、その後ろには何もないことを示さなければなりません。ドア 1 に留まると負けです。

シナリオ 3: ドア 1 を選択すると、賞品は実際にはドア 3 の後ろにあります。

この場合、モンティはドア 2 を開け、その後ろには何もないことを示さなければなりません。ドア 1 に留まると負けです。

これらはすべて、ドア 1 を選択した場合に考えられる結果です。ドア 1 を選択した場合、節約できる時間は 3 分の 1 だけであることに注意してください。しかし、変更すると 3 分の 2 の時間を節約できます。

次の表は、このゲーム ショーで考えられるすべてのシナリオと、維持および変更に関連する結果をまとめたものです。

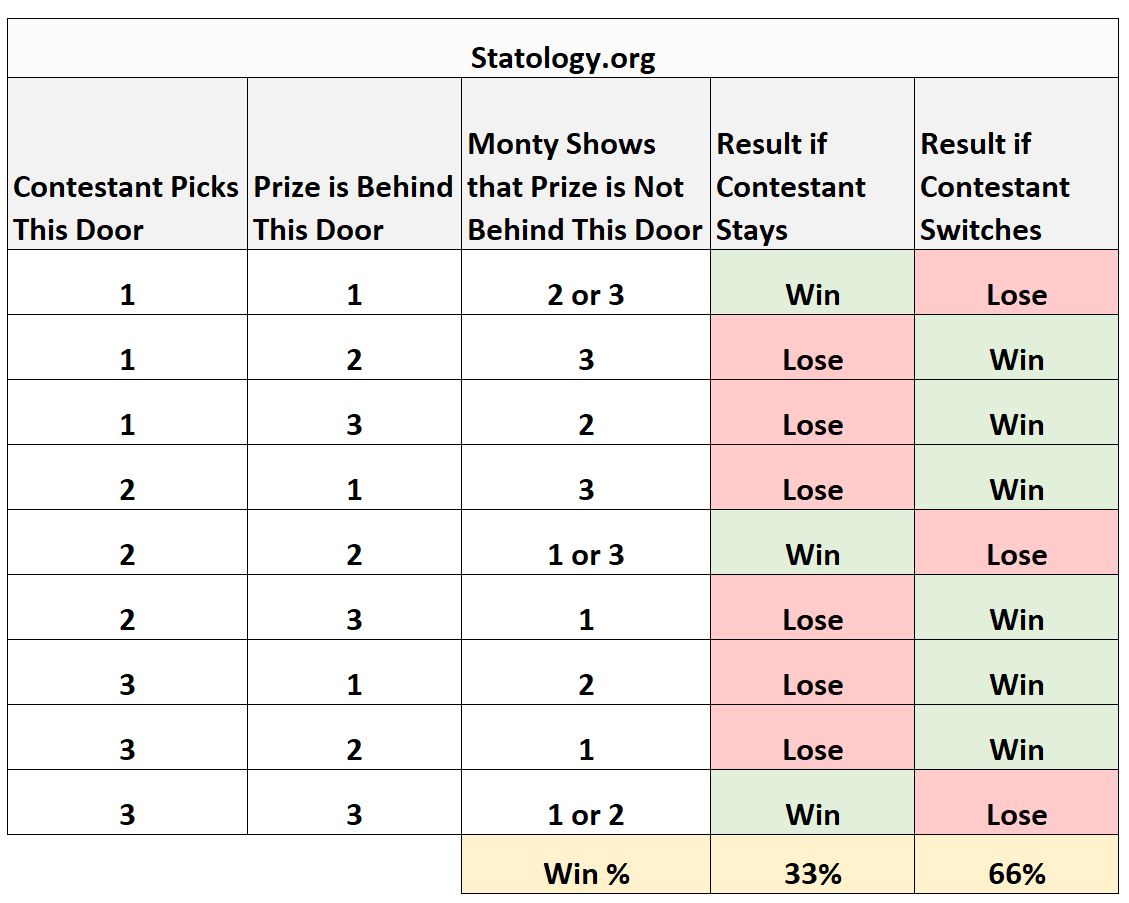
表から、滞在している場合は33%の確率で勝ちますが、切り替えた場合は66%の確率で勝ちます。

したがって、ドアを変更すると、賞品を獲得する可能性が高くなります。

これは直感的には意味がないと思われるかもしれませんが、数学は嘘をつきません。