ロジスティック回帰と線形回帰: 主な違い
最も一般的に使用される回帰モデルの 2 つは、線形回帰とロジスティック回帰です。
どちらのタイプの回帰モデルも、1 つ以上の予測変数と応答変数の間の関係を定量化するために使用されますが、2 つのモデルにはいくつかの重要な違いがあります。
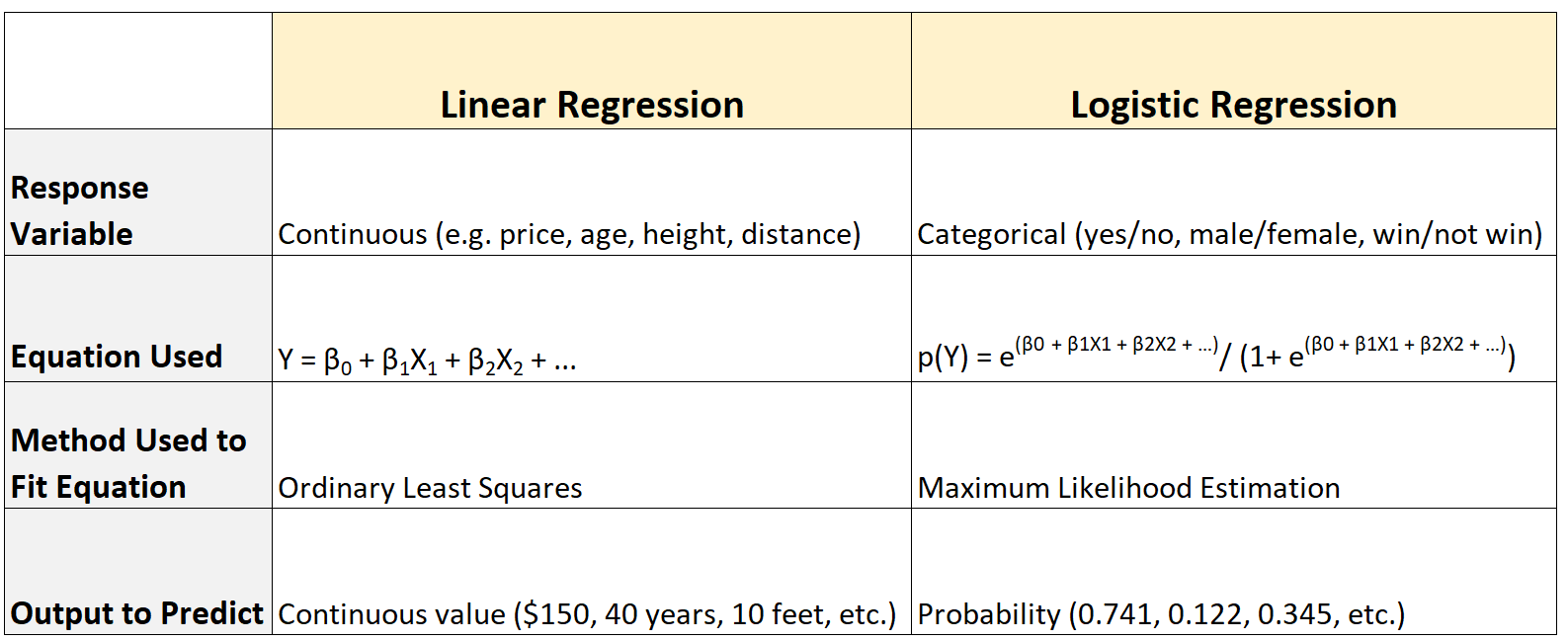
違いの概要は次のとおりです。
違い #1: 応答変数の型
線形回帰モデルは、応答変数が次のような連続値をとる場合に使用されます。
- 価格
- 身長
- 年
- 距離
逆に、ロジスティック回帰モデルは、応答変数が次のようなカテゴリ値を取る場合に使用されます。
- はい、もしくは、いいえ
- 男性か女性
- 勝つか勝たないか
違い #2: 使用される方程式
線形回帰では、次の方程式を使用して、予測変数と応答変数の間の関係を要約します。
Y = β 0 + β 1 X 1 + β 2 X 2 + … + β p
金：
- Y: 応答変数
- X j : j番目の予測変数
- β j : 他のすべての予測子を固定したまま、X jの 1 単位増加が Y に与える平均効果
逆に、ロジスティック回帰では次の方程式が使用されます。
p(X) = e β 0 + β 1 X 1 + β 2 X 2 + … + β p
この方程式は、個々の観測値が特定のカテゴリに分類される確率を予測するために使用されます。
違い #3: 方程式を当てはめるために使用される方法
線形回帰では、通常の最小二乗法として知られる方法を使用して、最適な回帰式を見つけます。
逆に、ロジスティック回帰では、最尤推定として知られる方法を使用して、最適な回帰式を見つけます。
違い #4: 予測される出力
線形回帰は、出力として連続値を予測します。例えば：
- 価格（150ドル、199ドル、400ドルなど）
- 高さ (14 インチ、2 フィート、94.32 センチメートルなど)
- 年齢（2ヶ月、6歳、41.5歳など）
- 距離 (1.23 マイル、4.5 キロメートルなど)
逆に、ロジスティック回帰は結果として確率を予測します。例えば：
- 大学に合格する確率は40.3％。
- 試合に勝つ確率は93.2%。
- 法案が採択される確率は34.2％。
ロジスティック回帰または線形回帰をいつ使用するか
次の練習問題は、ロジスティック回帰または線形回帰をいつ使用するかをより深く理解するのに役立ちます。
問題1: 年収
経済学者が、(1) 週間労働時間と (2) 教育年数を予測変数として使用して、個人の年収を予測したいとします。
このシナリオでは、応答変数 (年収) が連続であるため、線形回帰を使用します。
問題 #2: 大学への合格
大学の入学担当者が、予測変数 (1) GPA と (2) ACT スコアを使用して、学生が特定の大学に合格する可能性を予測したいとします。
このシナリオでは、応答変数がカテゴリ変数であり、受け入れられるか受け入れられないという 2 つの値しかとれないため、彼女はロジスティック回帰を使用します。
問題 #3: 不動産価格
不動産業者が、(1) 平方フィート、(2) 寝室の数、(3) バスルームの数という予測変数を使用して、住宅の販売価格を予測したいとします。
このシナリオでは、応答変数 (価格) が連続であるため、彼女は線形回帰を使用します。
問題 #4: スパムの検出
コンピューター プログラマーが、予測変数 (1) 単語数と (2) 発信国を使用して、特定の電子メールがスパムである確率を予測したいとします。
このシナリオでは、応答変数がカテゴリカルであり、スパムか非スパムかの 2 つの値しかとれないため、ロジスティック回帰が使用されます。
追加リソース
次のチュートリアルでは、線形回帰について詳しく説明します。
次のチュートリアルでは、ロジスティック回帰について詳しく説明します。
著者について
ベンジャミン・アンダーソン博士
私はベンジャミンです。退職した統計教授から、専任の Statorials 教育者になりました。 統計分野における豊富な経験と専門知識を活かして、私は Statorials を通じて学生に力を与えるために自分の知識を共有することに尽力しています。もっと知る