ロジスティック回帰
この記事では、統計におけるロジスティック回帰とは何かについて説明します。同様に、ロジスティック回帰の式、ロジスティック回帰のさまざまな種類、さらにロジスティック回帰の解決済み演習も見つかります。
ロジスティック回帰とは何ですか?
統計学において、ロジスティック回帰は、カテゴリ変数の結果を予測するために使用される回帰モデルの一種です。つまり、ロジスティック回帰を使用して、独立変数に基づいてカテゴリ変数が特定の値を取る確率をモデル化します。
最も一般的なロジスティック回帰モデルはバイナリ ロジスティック回帰で、考えられる結果は「失敗」または「成功」の 2 つだけです (ベルヌーイ分布)。 「失敗」は値 0 で表され、「成功」は値 1 で表されます。
たとえば、学生が勉強に費やした時間に基づいて試験に合格する確率は、ロジスティック回帰モデルを使用して調査できます。この場合、失敗は「失敗」の結果、成功は「成功」の結果ということになります。
ロジスティック回帰式
ロジスティック回帰モデルの方程式は次のとおりです。
![]()
したがって、ロジスティック回帰モデルでは、「成功」結果が得られる確率、つまり従属変数の値が 1 になる確率は次の式で計算されます。
![]()
金:
-

従属変数が 1 である確率です。
-

ロジスティック回帰モデルの定数です。
-

変数 i の回帰係数です。
-

変数 i の値です。
ロジスティック回帰モデルの例
ロジスティック回帰の定義を理解したところで、このタイプの回帰のモデルを作成する方法の具体例を見てみましょう。
- 次の表では、各生徒の学習時間と統計試験の合否を関連付ける一連の 20 個のデータが編集されています。ロジスティック回帰モデルを実行し、学生が 4 時間勉強した場合に合格する確率を計算します。
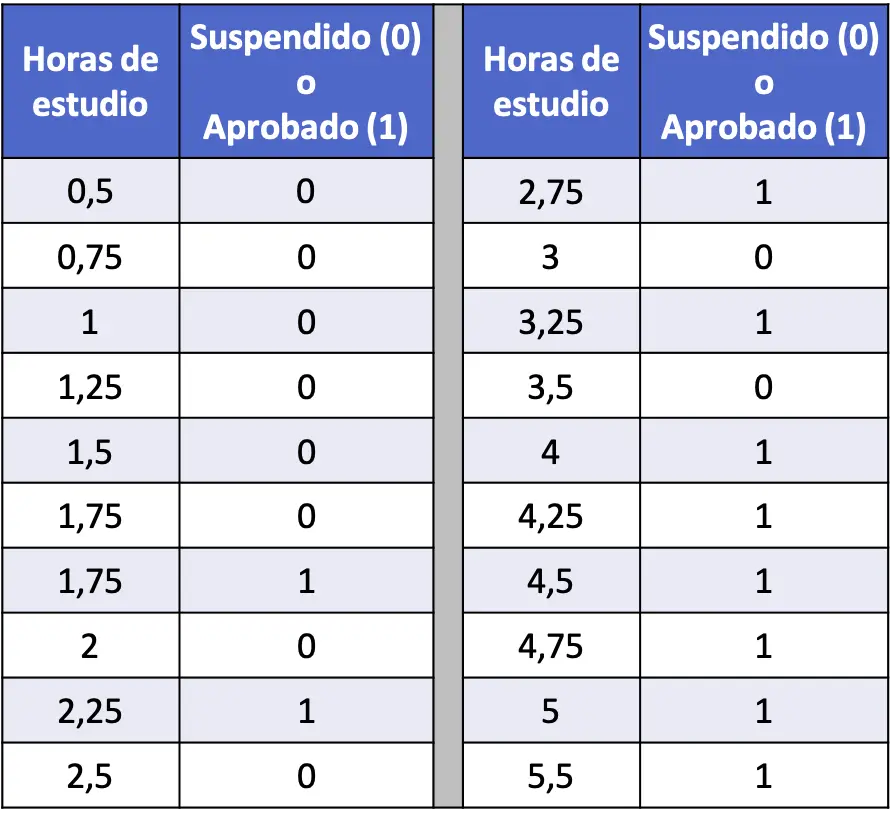
この場合、説明変数は学習時間数、応答変数は生徒が不合格 (0) か合格 (1) かです。したがって、私たちのモデルには係数のみが含まれます。
![]()
そして係数
![]()
独立変数が 1 つしかないためです。
![]()
回帰係数を手動で決定するのは非常に手間がかかるため、Minitab などのコンピュータ ソフトウェアを使用することをお勧めします。したがって、Minitabを使用して計算された回帰係数の値は次のとおりです。
![Rendered by QuickLaTeX.com \begin{array}{c}\beta_0\approx -4,1\\[2ex]\beta_1\approx 1,5\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-6ed66de602220c69aabb71a726fec9f8_l3.png)
したがって、ロジスティック回帰モデルは次のようになります。
![Rendered by QuickLaTeX.com \begin{aligned}p&=\cfrac{1}{1+e^{-(\beta_0+\beta_1x_1+\beta_2x_2+\dots+\beta_ix_i)}}\\[2ex]p&=\cfrac{1}{1+e^{-(-4,1+1,5x_1)}}\\[2ex]p&=\cfrac{1}{1+e^{4,1-1,5x_1}}\end{aligned}](https://statorials.org/wp-content/ql-cache/quicklatex.com-0902ac67194bedf38d5f4ff06dc27a38_l3.png)
以下に、サンプル データとロジスティック回帰モデル方程式をグラフ化したものを示します。
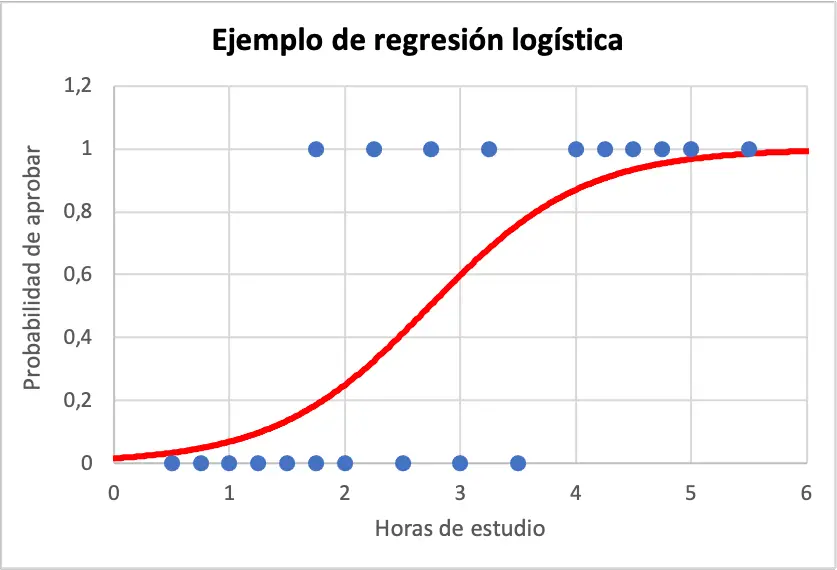
したがって、生徒が 4 時間勉強した場合に合格する確率を計算するには、ロジスティック回帰モデルから得られた式を使用するだけです。
![Rendered by QuickLaTeX.com \begin{aligned}p&=\cfrac{1}{1+e^{4,1-1,5x_1}}\\[2ex]p&=\cfrac{1}{1+e^{4,1-1,5\cdot 4}}\\[2ex]p&=0,8699\end{aligned}](https://statorials.org/wp-content/ql-cache/quicklatex.com-930691eafee62c04e59d9c4de8ef6a76_l3.png)
つまり、学生が 4 時間勉強した場合、86.99% の確率で試験に合格することになります。
ロジスティック回帰の種類
ロジスティック回帰には 3 つのタイプがあります。
- バイナリ ロジスティック回帰: 従属変数は 2 つの値 (0 と 1) のみを持つことができます。
- 多項ロジスティック回帰: 従属変数には 3 つ以上の可能な値があります。
- 順序ロジスティック回帰: 考えられる結果には自然な順序があります。
ロジスティック回帰と線形回帰
最後に、要約として、統計学で最もよく使用される回帰モデルは線形モデルであるため、ロジスティック回帰と線形回帰の違いを見ていきます。
線形回帰は、数値従属変数をモデル化するために使用されます。さらに、線形回帰では、説明変数と応答変数の間の関係は線形です。
したがって、ロジスティック回帰と線形回帰の主な違いは、従属変数のタイプです。ロジスティック回帰では従属変数はカテゴリ変数ですが、線形回帰では従属変数は数値です。
したがって、ロジスティック回帰は 2 つの可能な選択肢の間の結果を予測するために使用され、線形回帰は数値的な結果を予測するのに役立ちます。