Python でロジスティック回帰を実行する方法 (ステップバイステップ)

ロジスティック回帰は、 応答変数がバイナリの場合に回帰モデルを近似するために使用できる方法です。

ロジスティック回帰では、最尤推定として知られる方法を使用して、次の形式の方程式を求めます。

log[p(X) / ( ₁ -p(X))] = β ₀ + β ₁ X ₁ + β ₂ X ₂ + … + β _p

金：

• X _j : j^番目の予測変数
• β _j : j^番目の予測変数の係数の推定

方程式の右側の式は、応答変数が値 1 をとる対数オッズを予測します。

したがって、ロジスティック回帰モデルを当てはめる場合、次の方程式を使用して、特定の観測値が値 1 を取る確率を計算できます。

p(X) = e ^{β ₀ + _{β 1 X 1 + β 2 X 2 + … + β}} p

次に、特定の確率しきい値を使用して、観測値を 1 または 0 に分類します。

たとえば、確率が 0.5 以上の観測値は「1」に分類され、その他の観測値はすべて「0」に分類されると言えます。

このチュートリアルでは、R でロジスティック回帰を実行する方法の段階的な例を示します。

ステップ 1: 必要なパッケージをインポートする

まず、Python でロジスティック回帰を実行するために必要なパッケージをインポートします。

 import pandas as pd
import numpy as np
from sklearn. model_selection import train_test_split
from sklearn. linear_model import LogisticRegression
from sklearn import metrics
import matplotlib. pyplot as plt

ステップ 2: データをロードする

この例では、 書籍『統計学習入門』のデフォルトデータセットを使用します。次のコードを使用して、データセットの概要を読み込んで表示できます。

 #import dataset from CSV file on Github
url = "https://raw.githubusercontent.com/Statorials/Python-Guides/main/default.csv"
data = pd. read_csv (url)

#view first six rows of dataset
data[0:6]

        default student balance income
0 0 0 729.526495 44361.625074
1 0 1 817.180407 12106.134700
2 0 0 1073.549164 31767.138947
3 0 0 529.250605 35704.493935
4 0 0 785.655883 38463.495879
5 0 1 919.588530 7491.558572  

#find total observations in dataset
len( data.index )

10000

このデータセットには、10,000 人の個人に関する次の情報が含まれています。

• デフォルト:個人がデフォルトしたかどうかを示します。
• 学生:個人が学生であるかどうかを示します。
• 残高:個人が保有する平均残高。
• 収入：個人の収入。

学生のステータス、銀行残高、収入を使用して、特定の個人が債務不履行になる確率を予測するロジスティック回帰モデルを構築します。

ステップ 3: トレーニングおよびテストのサンプルを作成する

次に、データセットを、モデルをトレーニングするためのトレーニング セットと、モデルをテストするためのテスト セットに分割します。

 #define the predictor variables and the response variable
X = data[[' student ',' balance ',' income ']]
y = data[' default ']

#split the dataset into training (70%) and testing (30%) sets
X_train,X_test,y_train,y_test = train_test_split (X,y,test_size=0.3,random_state=0)

ステップ 4: ロジスティック回帰モデルを当てはめる

次に、 LogisticRegression()関数を使用して、ロジスティック回帰モデルをデータセットに適合させます。

 #instantiate the model
log_regression = LogisticRegression()

#fit the model using the training data
log_regression. fit (X_train,y_train)

#use model to make predictions on test data
y_pred = log_regression. predict (X_test)

ステップ 5: モデルの診断

回帰モデルを適合させたら、テスト データセットでのモデルのパフォーマンスを分析できます。

まず、モデルの混同行列を作成します。

 cnf_matrix = metrics. confusion_matrix (y_test, y_pred)
cnf_matrix

array([[2886, 1],
       [113,0]])

混同行列から次のことがわかります。

• #真陽性予測: 2886
• #真陰性予測: 0
• #誤検知予測: 113
• #偽陰性予測: 1

また、モデルによって行われた修正予測の割合を示す精度モデルを取得することもできます。

 print(" Accuracy: ", metrics.accuracy_score (y_test, y_pred))l

Accuracy: 0.962

これは、個人が96.2%の確率でデフォルトするかどうかについて、モデルが正しい予測を行ったことを示しています。

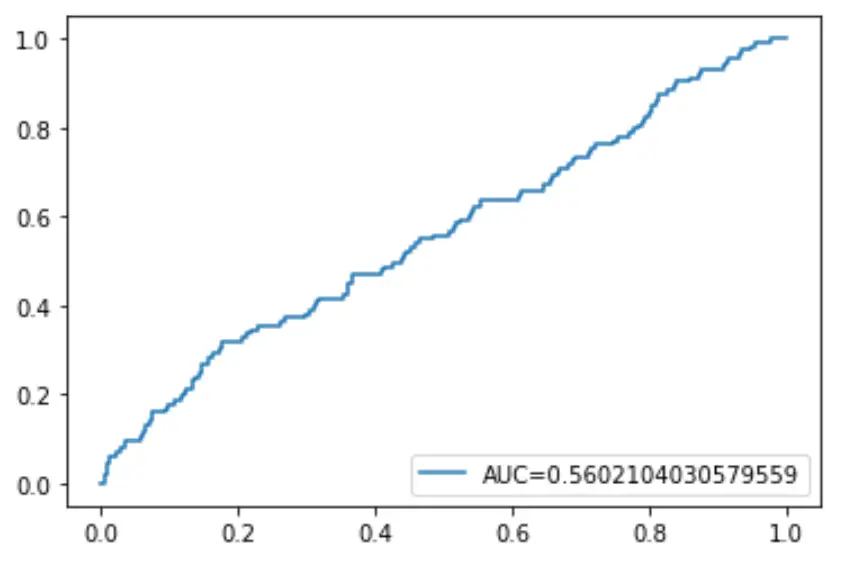
最後に、予測確率のしきい値を 1 から 0 に下げた場合に、モデルによって予測される真陽性の割合を表示する受信者動作特性 (ROC) 曲線をプロットできます。

AUC (曲線下面積) が高いほど、モデルはより正確に結果を予測できます。

 #define metrics
y_pred_proba = log_regression. predict_proba (X_test)[::,1]
fpr, tpr, _ = metrics. roc_curve (y_test, y_pred_proba)
auc = metrics. roc_auc_score (y_test, y_pred_proba)

#create ROC curve
plt. plot (fpr,tpr,label=" AUC= "+str(auc))
plt. legend (loc=4)
plt. show ()