Sas で一元配置分散分析を実行する方法

一元配置分散分析は、 3 つ以上の独立したグループの平均間に統計的に有意な差があるかどうかを判断するために使用されます。

このチュートリアルでは、SAS で一元配置 ANOVA を実行する方法のステップバイステップの例を示します。

ステップ 1: データを作成する

研究者が研究に参加する 30 人の学生を募集するとします。学生は、試験の準備のために 3 つの学習方法のいずれかを使用するようにランダムに割り当てられます。

各生徒の試験結果は以下のとおりです。

次のコードを使用して、SAS でこのデータセットを作成できます。

 /*create dataset*/
data my_data;
    input Method $Score;
    datalines ;
At 78
At 81
At 82
At 82
At 85
At 88
At 88
At 90
B 81
B 83
B 83
B85
B 86
B 88
B90
B91
C 84
C 88
C 88
C 89
C 90
C 93
C 95
C 98
;
run ;

ステップ 2: 一元配置分散分析を実行する

次に、 proc ANOVA を使用して一元配置分散分析を実行します。

 /*perform one-way ANOVA*/
proc ANOVA data =my_data;
classMethod ;
modelScore = Method;
means Method / tukey cldiff ;
run ;

注: 一元配置分散分析からの全体的な p 値が統計的に有意である場合にTukey 事後検定を実行する必要があることを指定するために平均関数を使用しました。

ステップ 3: 結果を解釈する

結果で分析する最初のテーブルは ANOVA テーブルです。

この表から次のことがわかります。

• 全体のF値： 5.26
• 対応する p 値: 0.0140

一元配置分散分析では次の帰無仮説と対立仮説が使用されることを思い出してください。

• H ₀ :すべてのグループ平均が等しい。
• H _A :少なくとも 1 つのグループの平均が異なります 休む。

ANOVA 表の p 値 (0.0140) は α = 0.05 より小さいため、帰無仮説を棄却します。

これは、試験の平均点が 3 つの勉強方法で同じではないことを示しています。

関連: ANOVA で F 値と P 値を解釈する方法

SAS は、3 つの学習方法ごとの試験結果の分布を視覚化するための 箱ひげ図も提供します。

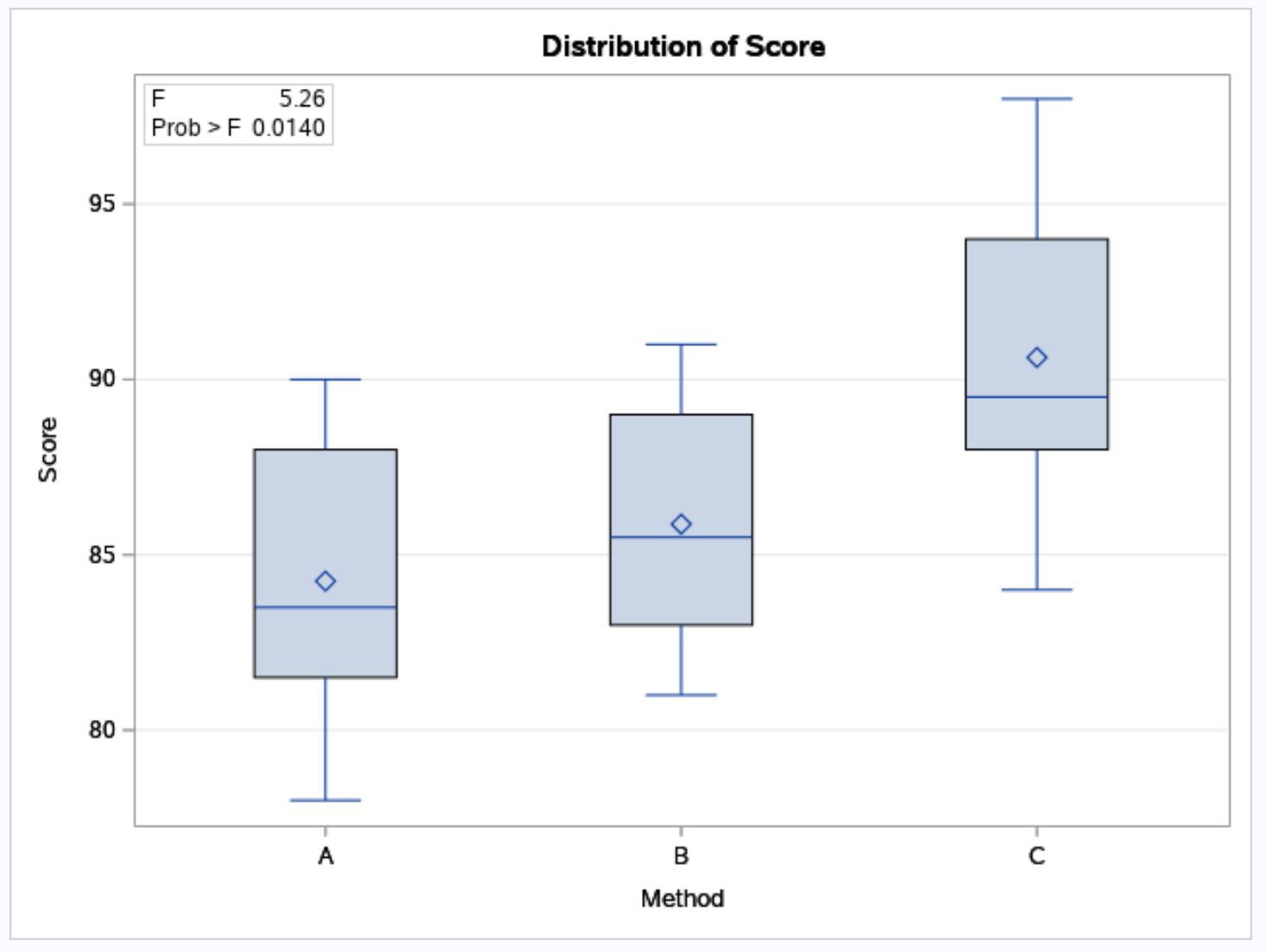
箱ひげ図から、方法 B および C と比較して、勉強方法 C を使用した生徒の試験の得点が高い傾向があることがわかります。

どのグループ平均が異なるかを正確に判断するには、Tukey の事後検定の結果を示す最終結果テーブルを参照する必要があります。

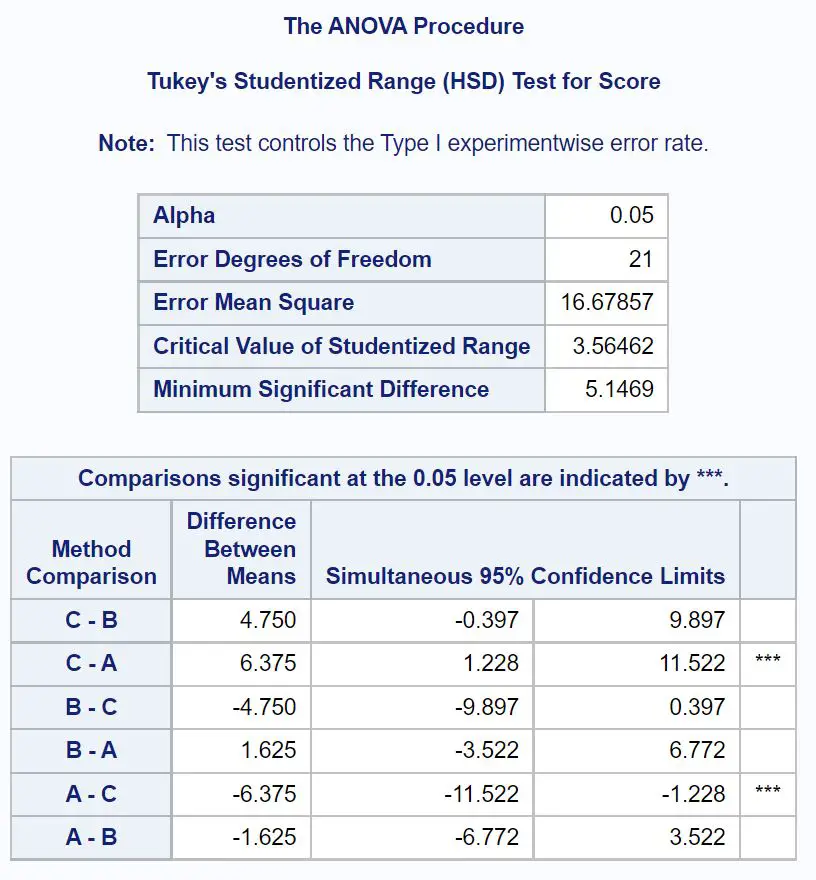
どのグループ平均が異なるかを調べるには、どのペアごとの比較の横に星 ( *** ) が付いているかを確認する必要があります。

表は、グループ A とグループ C の平均値が統計的に有意に異なることを示しています。

グループ A とグループ C の間の平均試験得点の差の 95% 信頼区間も確認できます。

平均差の 95% 信頼区間: [1.228, 11.522]

ステップ 4: 結果を報告する

最後に、一元配置分散分析の結果を報告します。

検査結果に対する 3 つの異なる研究方法の影響を比較するために、一元配置 ANOVA が実行されました。

一元配置分散分析により、少なくとも 2 つのグループ間で試験の平均得点に統計的に有意な差があることが明らかになりました (F(2,21) = [5.26]、p = 0.014)。

多重比較のための Tukey の HSD テストにより、試験スコアの平均値が方法 C と方法 A で有意に異なることが明らかになりました (95% CI = [1.228, 11.522])。

方法 A と方法 B の間、または方法 B と方法 C の間で、試験の平均スコアに統計的に有意な差はありませんでした。

追加リソース

次のチュートリアルでは、一元配置分散分析に関する追加情報を提供します。

一元配置分散分析の概要
一元配置分散分析計算機
一元配置分散分析を手動で実行する方法