Spss で一元配置分散分析を実行する方法

一元配置分散分析は、 3 つ以上の独立したグループの平均間に統計的に有意な差があるかどうかを判断するために使用されます。

このタイプの検定は、応答変数に対する予測変数の影響を分析するため、一元配置分散分析と呼ばれます。

代わりに、応答変数に対する2 つの予測変数の影響に興味がある場合は、二元配置 ANOVAを実行できます。

このチュートリアルでは、SPSS で一元配置分散分析を実行する方法について説明します。

例: SPSS での一元配置分散分析

研究者が研究に参加する 30 人の学生を募集するとします。学生は、翌月に試験の準備のために 3 つの学習テクニックのうち 1 つを使用するようにランダムに割り当てられます。月末に、生徒全員が同じテストを受けます。

学生のテスト結果は次のとおりです。

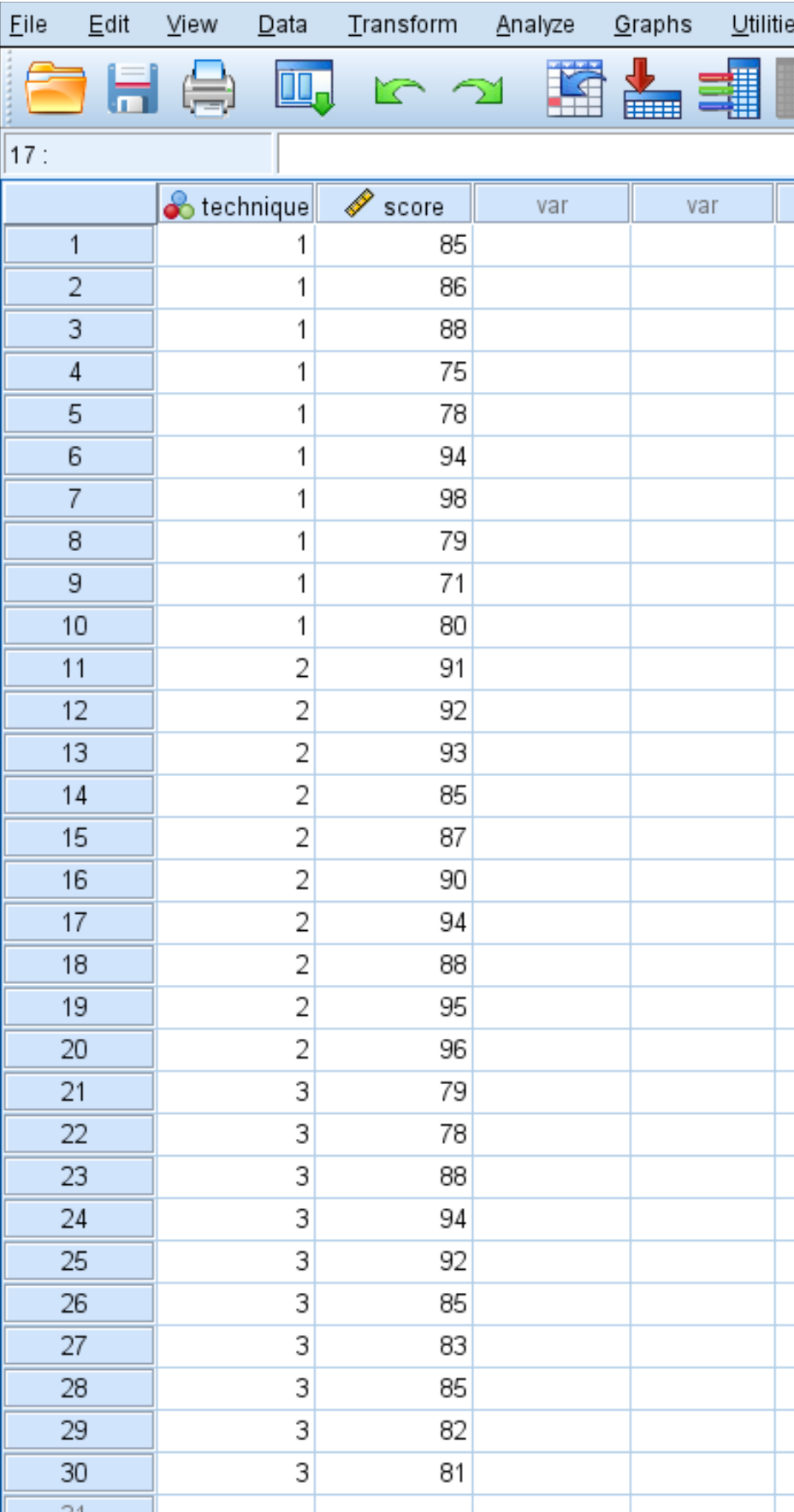
次の手順を使用して一元配置分散分析を実行し、平均スコアが 3 つのグループ間で同じかどうかを判断します。

ステップ 1: データを視覚化します。

まず、 箱ひげ図を作成して、3 つの学習手法ごとのテストのスコアの分布を視覚化します。 「グラフ」タブをクリックし、 「グラフビルダー」をクリックします。

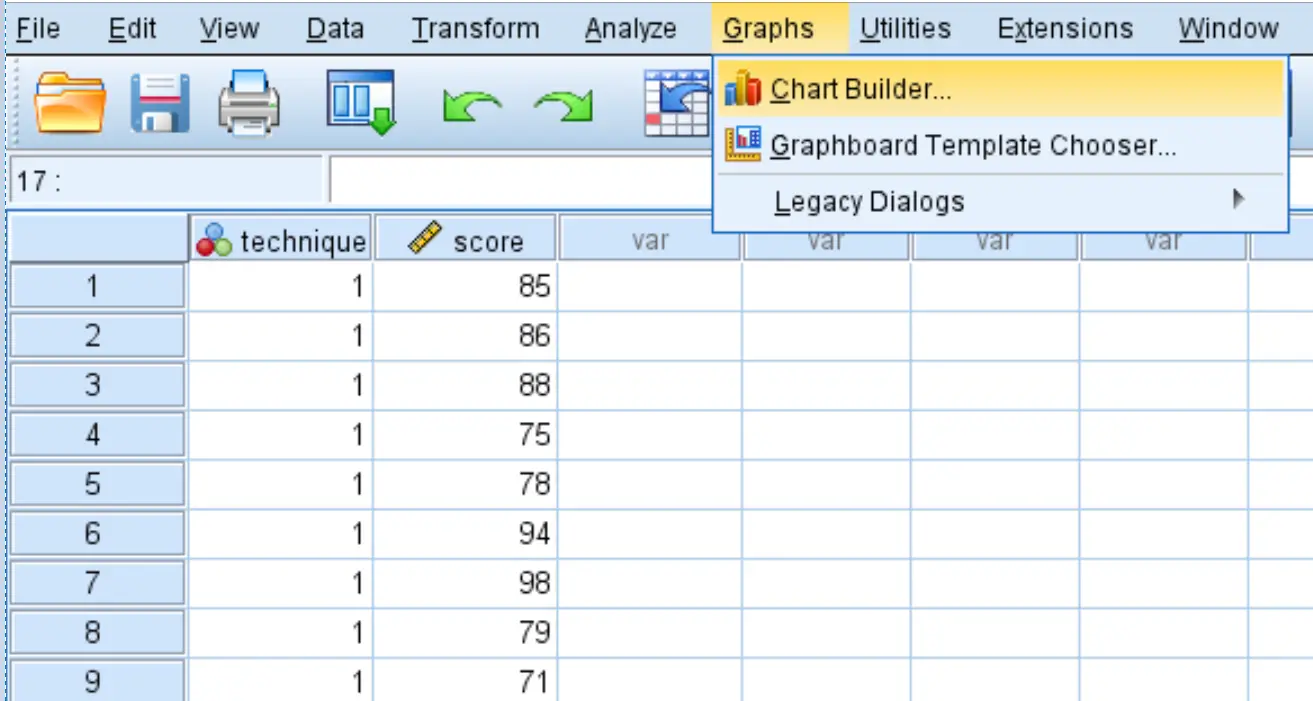
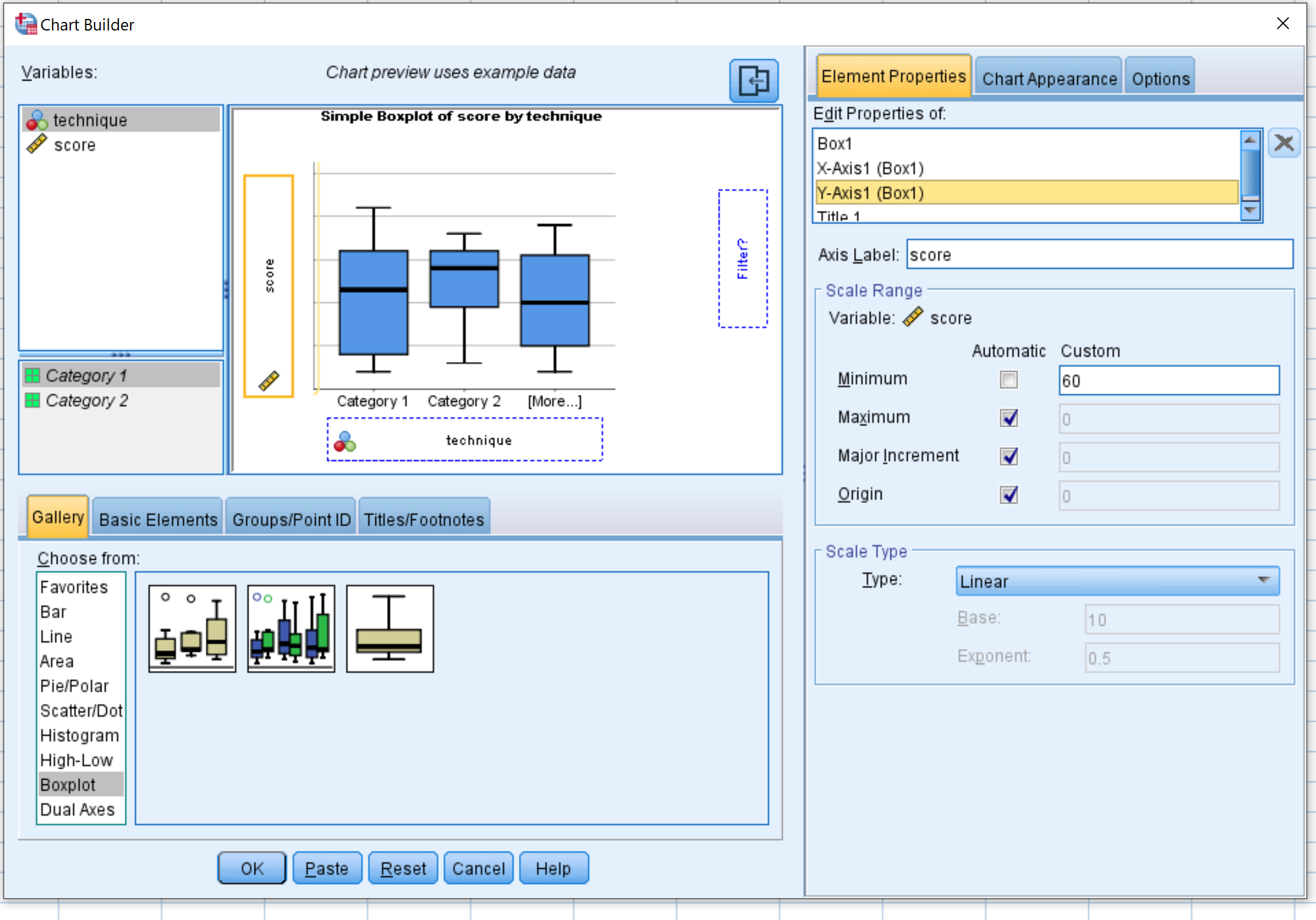
「次から選択:」ウィンドウで「箱ひげ図」を選択します。次に、 「Simple boxplot」というラベルが付いた最初のグラフをメイン編集ウィンドウにドラッグします。 X 軸上の技術変数と Y 軸上のスコアをドラッグします。

次に、 [要素プロパティ]をクリックし、 [Y1 軸] をクリックします。最小値を 60 に変更します。次に、 [OK]をクリックします。

次の箱ひげ図が表示されます。

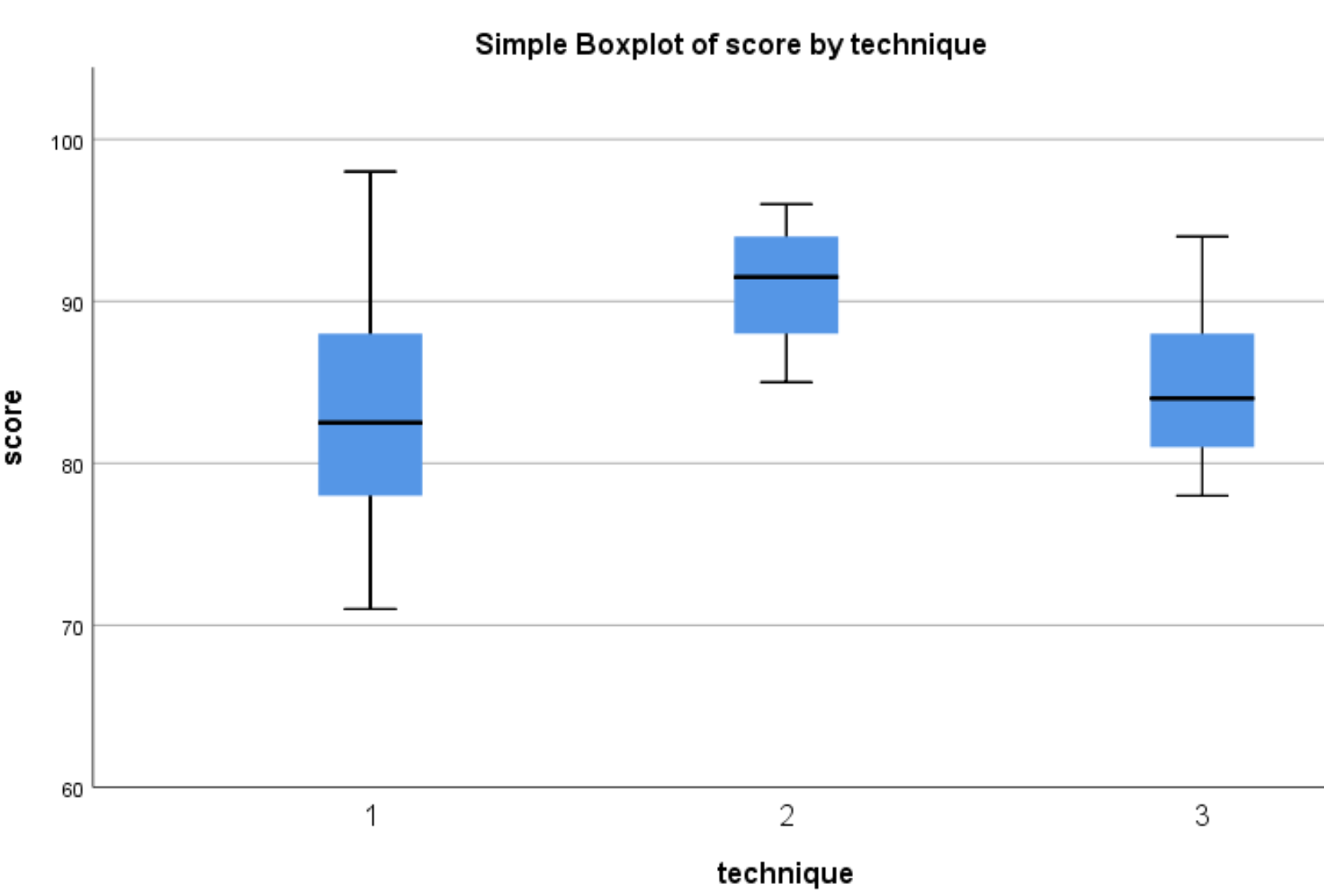
テストのスコアの分布は、テクニック 1 と 3 を使用した生徒よりもテクニック 2 を使用した生徒の方が高くなる傾向があることがわかります。これらのスコアの差が統計的に有意であるかどうかを判断するために、一元配置分散分析を実行します。

ステップ 2: 一元配置分散分析を実行します。

「分析」タブ、 「平均の比較」 、 「一元配置分散分析」の順にクリックします。

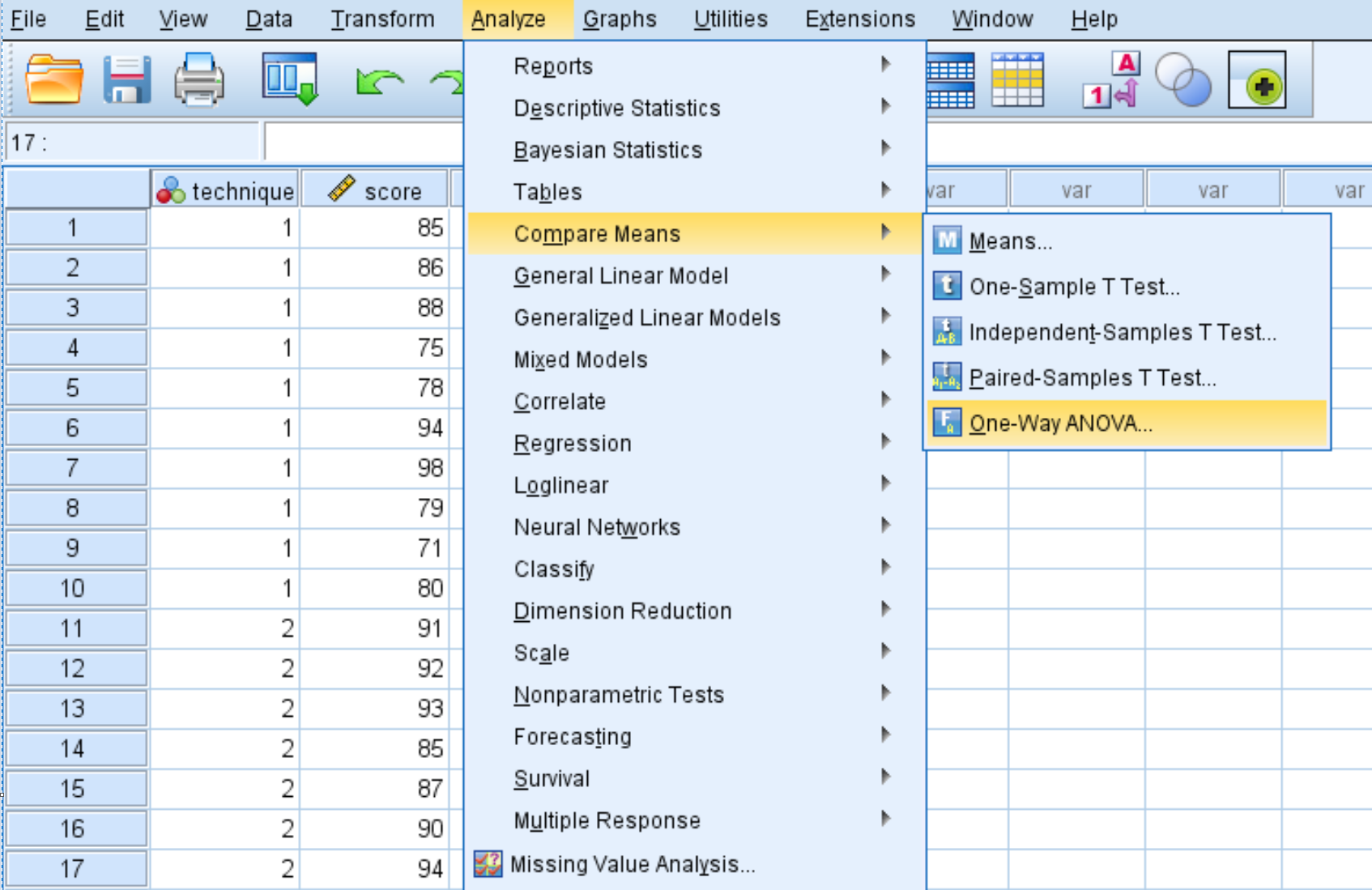
表示される新しいウィンドウで、変数スコアを「依存リスト」というラベルのボックスに配置し、変数テクニックを「因子」というラベルのボックスに配置します。

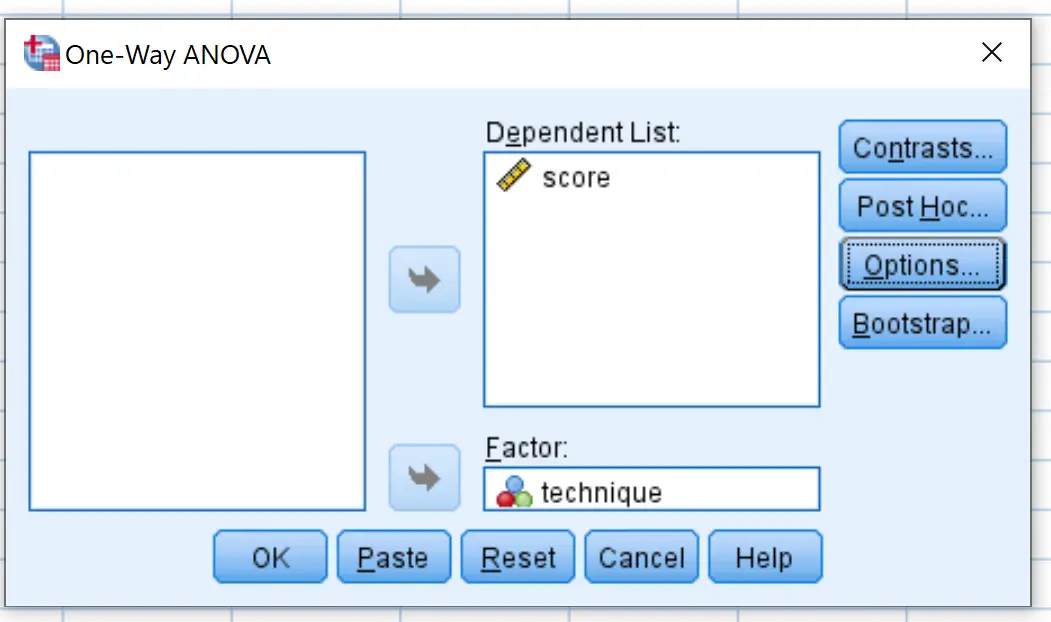
次に、 [Post Hoc]をクリックして、 Tukeyの横のボックスをオンにします。次に、 「続行」をクリックします。

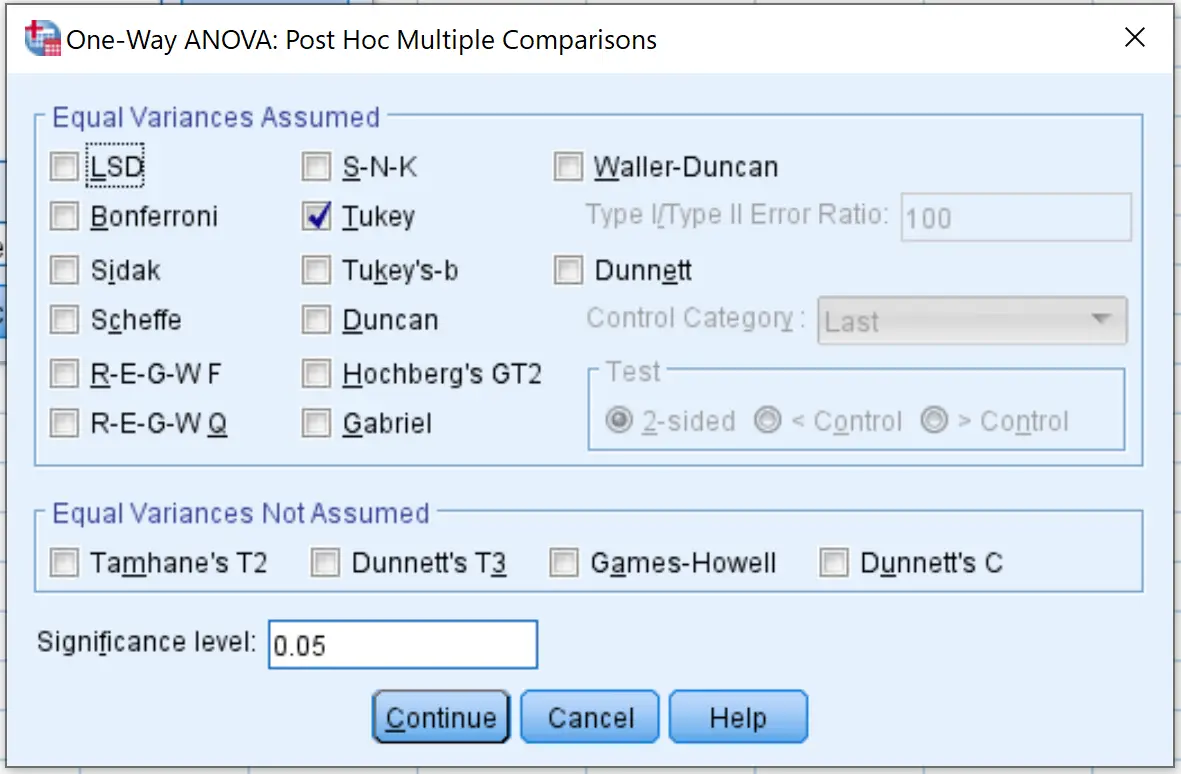
次に、 「オプション」をクリックし、 「説明」の横のボックスにチェックを入れます。次に、 「続行」をクリックします。

最後に、 「OK」をクリックします。

ステップ 3: 結果を解釈します。

[OK]をクリックすると、一元配置分散分析の結果が表示されます。結果を解釈する方法は次のとおりです。

テーブルの説明

この表には、データセット内の 3 つのグループごとの記述統計が表示されます。

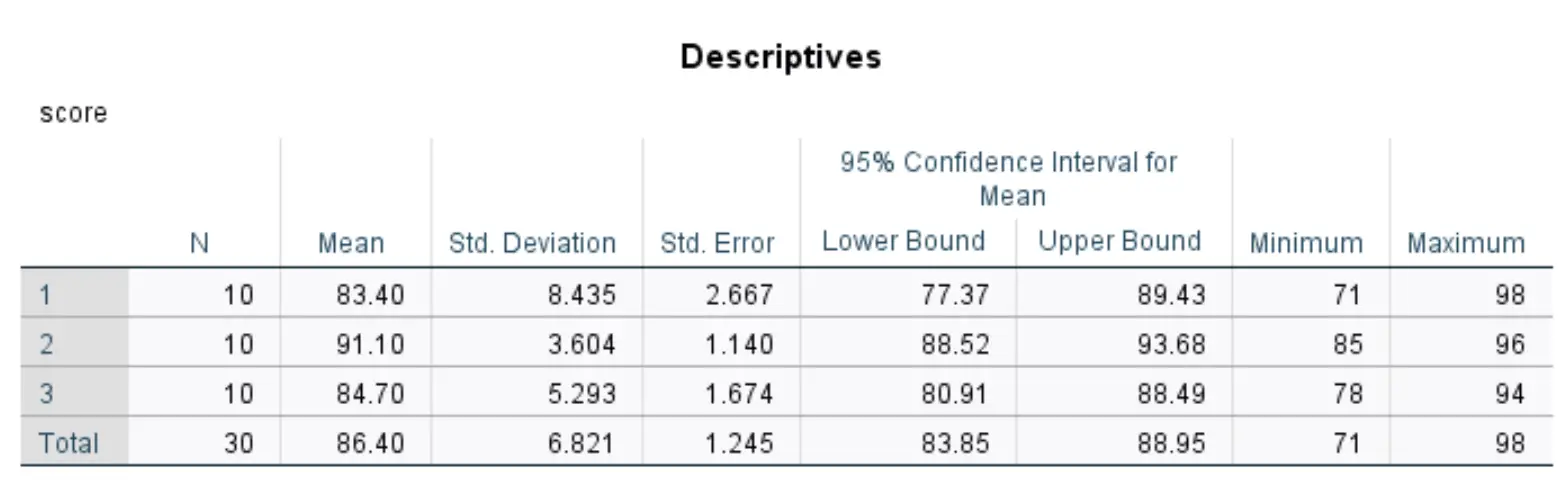
最も関連性の高い数字は次のとおりです。

• N:各グループの生徒の数。
• 平均:各グループのテストの平均スコア。
• 標準。偏差:各グループのテスト結果の標準偏差。

分散分析テーブル

この表には、一元配置分散分析の結果が表示されます。

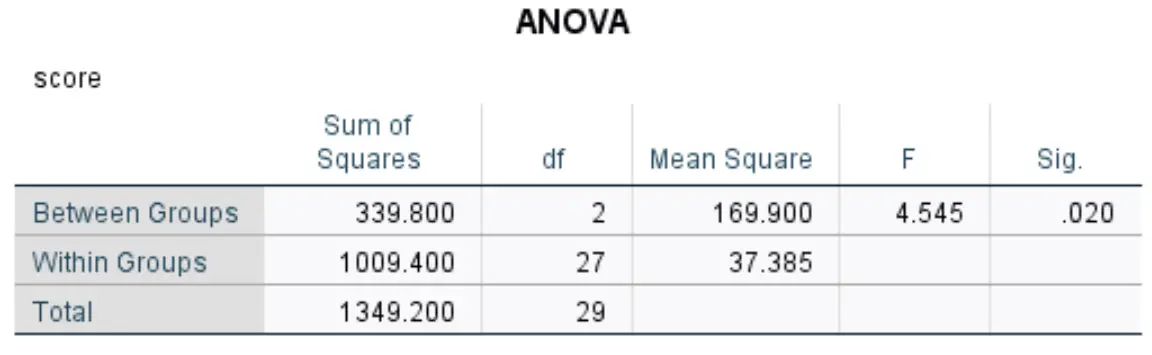
最も関連性の高い数字は次のとおりです。

• F:全体的な F 統計。
• Sig:分子 df (2) と分母 df (27) をもつ F 統計量 (4.545) に対応する p 値。この場合、p 値は0.020であることがわかります。

一元配置分散分析では次の帰無仮説と対立仮説が使用されることを思い出してください。

• H ₀ (帰無仮説): μ ₁ = μ ₂ = μ ₃ = … = μ _k (すべての母集団平均は等しい)
• H _A (対立仮説):少なくとも 1 つの母集団平均が異なる 休む

ANOVA 表の p 値は 0.05 未満であるため、帰無仮説を棄却し、グループ平均の少なくとも 1 つが他の平均とは異なると結論付けるのに十分な証拠があります。

どのグループ平均が互いに異なるかを正確に知るには、ANOVA 結果の最後の表を参照します。

多重比較表

この表は、3 つのグループそれぞれの間の Tukey の事後多重比較を表示します。私たちは主にシグに興味があります。列には、各グループ間の平均の差の p 値が表示されます。

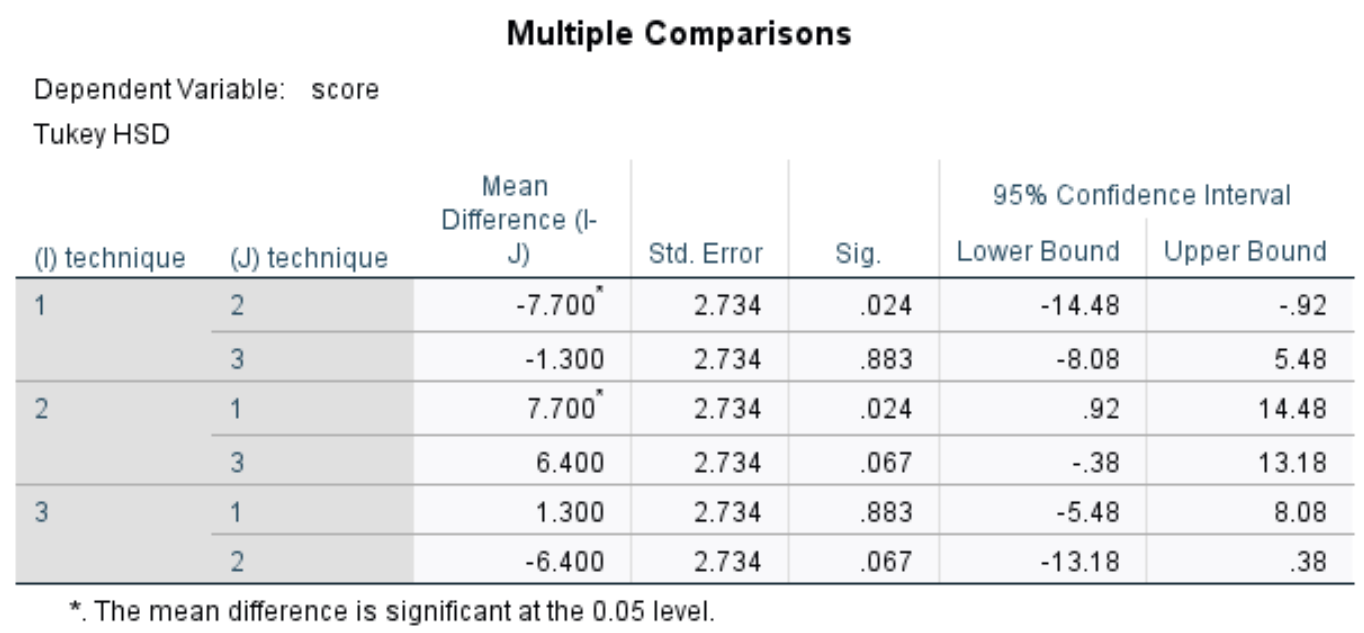
表では、次の比較の p 値を確認できます。

• テクニック 1 対 2: | p値 = 0.024
• テクニック 1 対 3 | p値 = 0.883
• テクニック 2 対 3 | p値 = 0.067

p 値が 0.05 未満の唯一のグループ比較は、テクニック 1 とテクニック 2 の間です。

これは、テクニック 1 を使用した生徒とテクニック 2 を使用した生徒の間で、テストの平均点に統計的に有意な差があることがわかります。

ただし、手法 1 と手法 3 の間、または手法 2 と手法 3 の間に統計的に有意な差はありません。

ステップ 4: 結果を報告します。

最後に、一元配置分散分析の結果を報告します。これを行う方法の例を次に示します。

3 つの異なる研究手法が異なるテスト結果につながるかどうかを判断するために、一元配置 ANOVA が実行されました。

合計 10 人の学生が 3 つの学習テクニックをそれぞれ 1 か月間使用してから、全員が同じテストを受けました。

一元配置分散分析により、少なくとも 2 つのグループ間でテストのスコアに統計的に有意な差があることが明らかになりました (F(2, 27) = 4.545、p = 0.020)。

多重比較のための Tukey 検定により、テクニック 1 とテクニック 2 を使用した生徒の間でテストの平均スコアが大きく異なることが明らかになりました (p = 0.024、95% CI = [-14.48, -0.92])。

テクニック 1 と 3 のスコア間 (p = 0.883)、またはテクニック 2 と 3 のスコア間に (p = 0.067) 統計的に有意な差はありませんでした。