一様分布の概要
一様分布とは、 aからbまでの区間の間の各値が同じ確率で出現する確率分布です。
確率変数X が一様分布に従う場合、 Xがx 1とx 2の間の値を取る確率は、次の式で求められます。
P(x 1 < X < x 2 ) = (x 2 – x 1 ) / (b – a)
金:
- x 1 :低い方の利息額
- x 2 :対象の上限値
- a:可能な最小値
- b:取り得る最大値
たとえば、イルカの体重が 100 ポンドから 150 ポンドの間で均等に分布しているとします。
イルカをランダムに選択すると、上記の式を使用して、選択したイルカの体重が 120 ~ 130 ポンドである確率を求めることができます。
- P(120 < X < 130) = (130 – 120) / (150 – 100)
- P(120 < X < 130) = 10/50
- P(120 < X < 130) = 0.2
選ばれたイルカの体重が 120 ~ 130 ポンドである確率は0.2です。
一様分布の可視化
一様分布を視覚化するために密度プロットを作成すると、次のプロットのようになります。
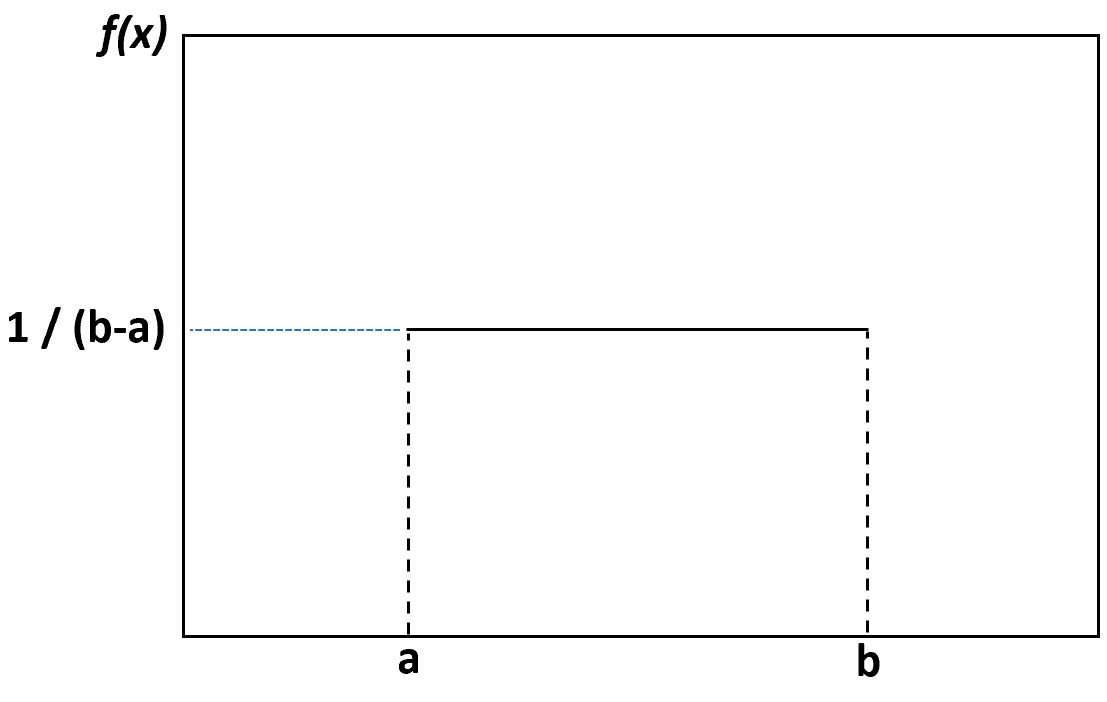
下限値aと上限値bの間のすべての値の発生確率は同じであり、これらの値の外側にある値の確率はゼロです。
たとえば、前の例では、イルカの体重は 100 ポンドから 150 ポンドの間で均等に分布していると言いました。この分布を視覚化する方法は次のとおりです。
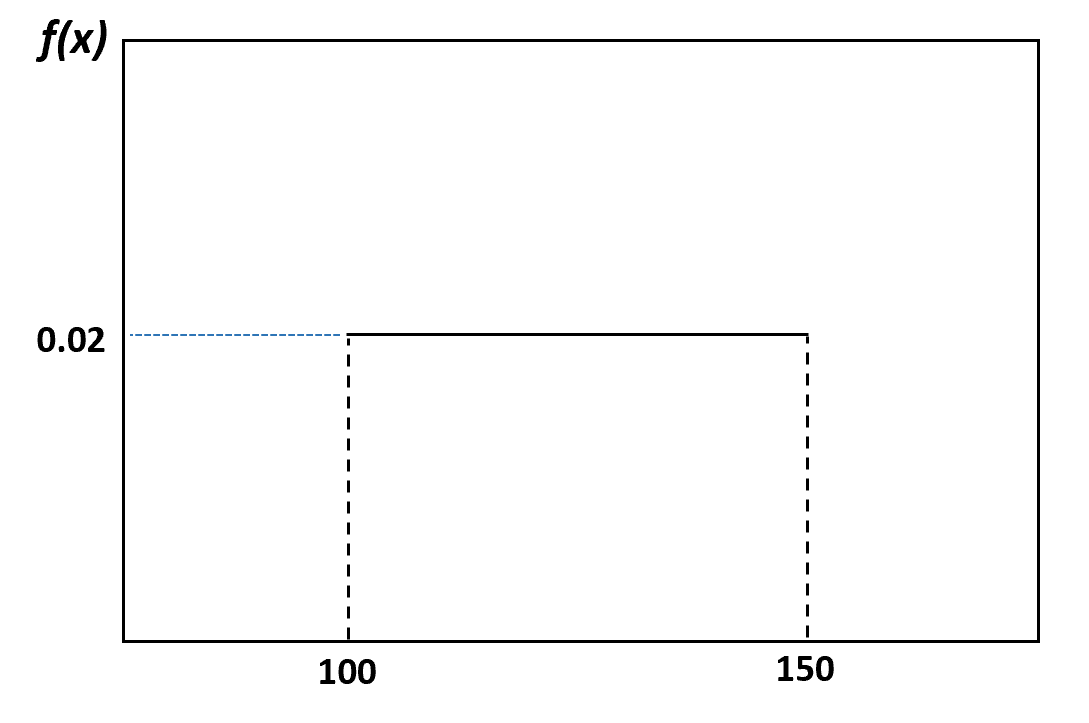
そして、ランダムに選択されたイルカの体重が 120 ~ 130 ポンドである確率は、次のように視覚化できます。
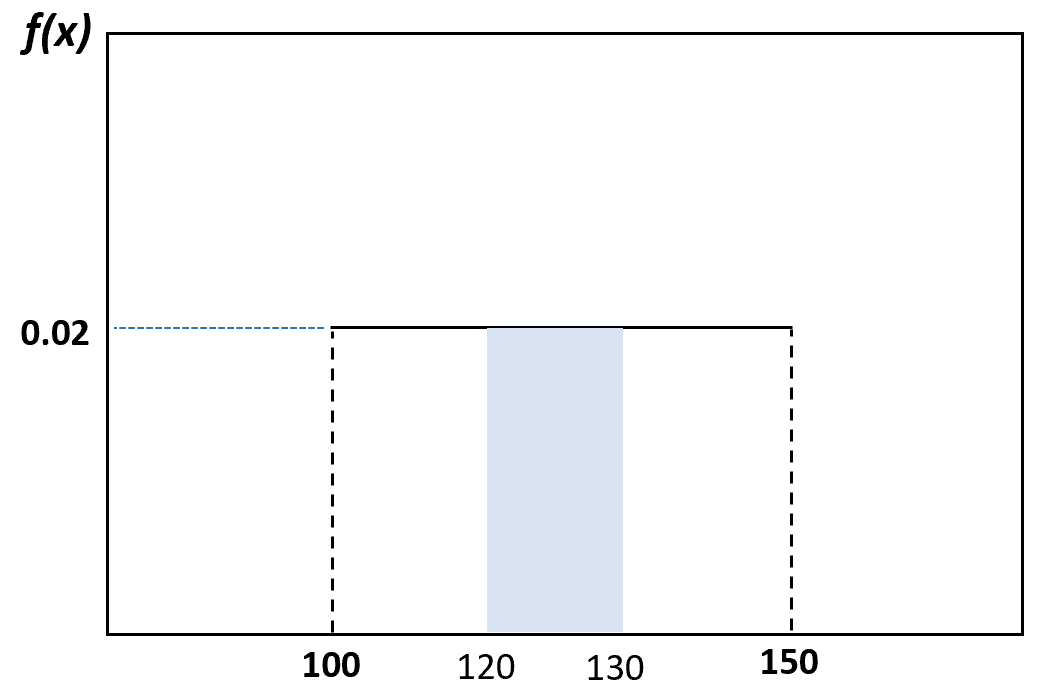
一様分布の性質
一様分布には次の特性があります。
- 平均: (a + b) / 2
- 中央値: (a + b) / 2
- 標準偏差: √ (b – a) 2 / 12
- 差: (b – a) 2 / 12
たとえば、イルカの体重が 100 ポンドから 150 ポンドの間で均等に分布しているとします。
この分布について次のプロパティを計算できます。
- 平均重量: (a + b) / 2 = (150 + 100) / 2 = 125
- 体重の中央値: (a + b) / 2 = (150 + 100) / 2 = 125
- 重量の標準偏差: √ (150 – 100) 2 / 12 = 14.43
- 重量変動: (150 – 100) 2 / 12 = 208.33
均一な配布慣行の問題
次の練習問題を使用して、一様分布に関する知識をテストしてください。
質問 1:バスは 20 分ごとにバス停に来ます。バス停に到着した場合、バスが 8 分以内に到着する確率はどれくらいですか?
解決策 1:最小待機時間は 0 分、最大待機時間は 20 分です。下限金利値は 0 分、上限金利値は 8 分です。
したがって、確率は次のように計算されます。
P(0 < X < 8) = (8-0) / (20-0) = 8/20 = 0.4 。
質問 2: NBA の試合時間は 120 ~ 170 分の間で均等に配分されます。ランダムに選択された NBA の試合が 155 分を超える確率はどれくらいですか?
解決策 2:最小期間は 120 分、最大期間は 170 分です。下限金利値は 155 分、上限金利値は 170 分です。
したがって、確率は次のように計算されます。
P(155 < X < 170) = (170-155) / (170-120) = 15/50 = 0.3 。
質問 3:特定の種のカエルの体重は 15 グラムから 25 グラムの間で均等に分布しています。カエルをランダムに選択した場合、その重さが 17 グラムから 19 グラムの間である確率はどれくらいですか?
解決策 3:最小重量は 15 グラム、最大重量は 25 グラムです。下限金利は 17 グラム、上限金利は 19 グラムです。
したがって、確率は次のように計算されます。
P(17 < X < 19) = (19-17) / (25-15) = 2/10 = 0.2 。
注:一様分布計算ツールを使用して、これらの問題のそれぞれに対する答えを確認できます。