Ti-84 電卓で中心極限定理を適用する方法
中心極限定理は、たとえ母集団の分布が正規でなくても、サンプルサイズが十分に大きければ標本平均の標本分布はほぼ正規になる、というものです。
中心極限定理は、標本分布が次の特性を持つことも示しています。
1.標本分布の平均は母集団分布の平均と等しくなります。
x = μ
2.標本分布の標準偏差は、母集団の標準偏差を標本サイズで割ったものとなります。
s = σ / √n
TI-84 計算機でサンプル平均に関連する確率を求めるには、次の構文でNormalcdf()関数を使用できます。
normalcdf (lower value, upper value, x , s/√ n )
金:
- x : サンプルの平均値
- s : サンプル標準偏差
- n : サンプルサイズ
TI-84 電卓でこの関数にアクセスするには、 2nd を押してからVARS を押し、 normalcdf までスクロールして (そしてENTERを押します) だけです。
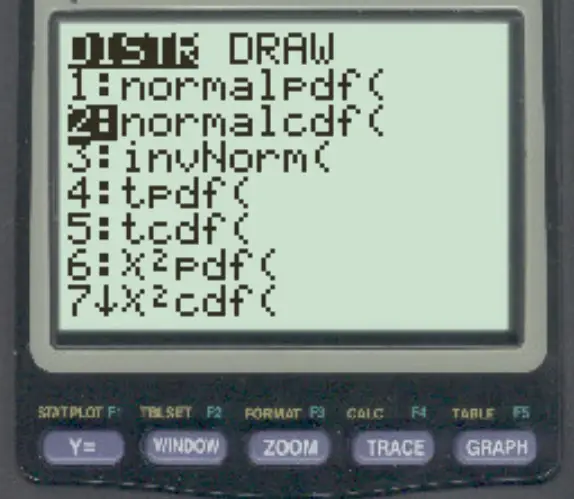
次の例は、この関数を実際に使用する方法を示しています。
例 1: 2 つの値の間の確率を求める
分布の平均は 70、標準偏差は 7 です。サイズ n = 35 のランダムなサンプルを選択した場合、サンプル平均が 68 ~ 72 の間にある確率を求めます。
TI-84 では次の構文を使用できます。
normalcdf (68, 72, 70, 7/√ 35 )
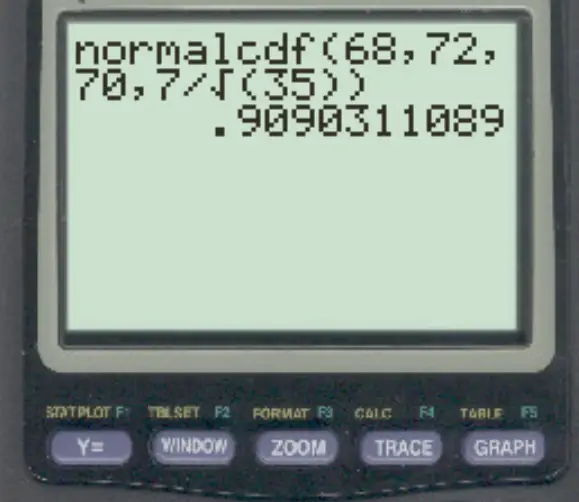
標本平均が 68 ~ 72 の間にある確率は0.909です。
例 2: 値よりも大きい確率を求める
分布の平均は 50、標準偏差は 4 です。サイズ n = 30 のランダムなサンプルを選択した場合、サンプルの平均が 48 より大きい確率を求めます。
TI-84 では次の構文を使用できます。
normalcdf (48, E99, 50, 4/√ 30 )
注: 2 を押してから , ボタンを押すと、「E」記号にアクセスできます。
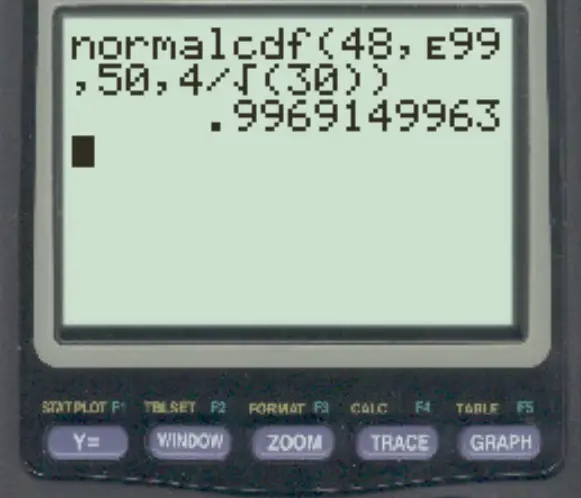
サンプル平均が 48 より大きい確率は0.9969です。
例 3: 値より小さい確率を求める
分布の平均は 20、標準偏差は 3 です。サイズ n = 40 の無作為サンプルを選択した場合、サンプル平均が 19 未満である確率を求めます。
TI-84 では次の構文を使用できます。
normalcdf (-E99, 19, 20, 3/√ 40 )
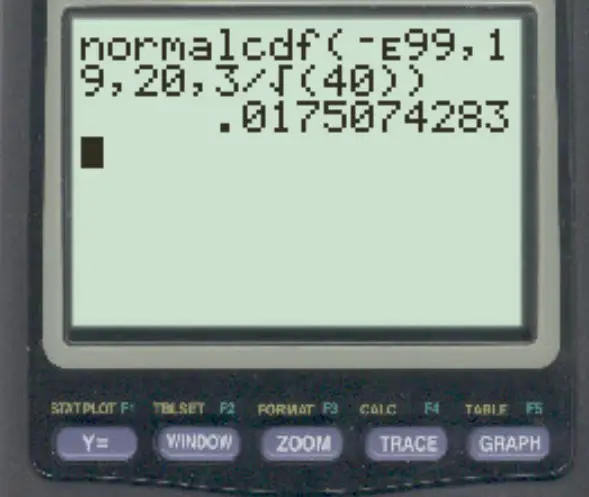
サンプル平均が 19 未満である確率は0.0175です。