中程度の差

によるベンジャミン・アンダーソン博士 8月 5, 2023 統計 0コメント

この記事では、平均偏差とは何か、その計算方法について説明します。平均偏差の計算の具体例も紹介します。さらに、オンライン計算機を使用して、統計データセットの平均偏差を計算できるようになります。

平均偏差とは何ですか?

平均偏差は、平均絶対偏差とも呼ばれ、統計的分散の尺度です。

データセットの平均偏差は、絶対偏差の平均です。したがって、平均偏差は、算術平均からの各データ項目の偏差の合計をデータ項目の総数で割ったものに等しくなります。

つまり、平均偏差の式は次のようになります。

👉以下の計算機を使用して、任意のデータセットの平均偏差を計算できます。

統計学では、平均偏差は平均絶対偏差とも呼ばれます。

平均偏差の解釈は次のように行われます。平均偏差の値が大きいほど、データが平均して算術平均から離れていることを意味します。逆に、平均偏差が低いほど、値は近づきます。データは。したがって、平均偏差はデータ系列の分散を示します。

分布しているとみなされるその他の尺度には、範囲、四分位範囲、標準偏差 (または標準偏差)、分散、および変動係数があります。

平均偏差の計算方法

データ系列の平均偏差を計算するには、次の手順に従う必要があります。

統計データセットの算術平均を計算します。
平均からの各データポイントの偏差を計算します。これは、データと平均の差の絶対値として定義されます。
前のステップで計算されたすべての差を合計します。
データの総数で割ります。得られる結果は、データ系列の平均偏差です。

要約すると、平均偏差を求めるために適用する必要がある公式は次のとおりです。

$D_{\overline{x}}=\cfrac{\sum_{i=1}^N|x_i-\overline{x}|}{N}$

平均偏差の計算例

平均偏差の定義を考慮して、統計サンプルの平均偏差を計算する段階的な解決例を以下に示します。こうすることで、平均偏差を取得する方法をよりよく理解できるようになります。

アナリストは過去 1 年間の企業の経済成績を調査し、その年の各四半期に企業が得た利益 (200 万ドル、300 万ドル、700 万ドル、500 万ドル) に関する情報を入手します。データの平均偏差はどれくらいですか?

まず、データを平均する必要があるため、合計して観測値の総数で割ります (4)。

$\overline{x}=\cfrac{2+3+7+5}{4}=4,25$

算術平均を計算したら、平均偏差の式を使用します。

$D_{\overline{x}}=\cfrac{\sum_{i=1}^N|x_i-\overline{x}|}{N}$

データを式に代入します。

$D_{\overline{x}}=\cfrac{|2-4,25|+|3-4,25|+|7-4,25|+|5-4,25|}{4}$

分子で計算を行います。

$D_{\overline{x}}=\cfrac{|-2,25|+|-1,25|+|2,75|+|0,75|}{4}$

$D_{\overline{x}}=\cfrac{2,25+1,25+2,75+0,75}{4}$

$D_{\overline{x}}=\cfrac{7}{4}$

最後に、データの総数で割って、サンプルの平均偏差を取得します。

$D_{\overline{x}}=1,75$

平均偏差計算機

一連の統計データを次の計算機に入力して、その平均偏差を計算します。データはスペースで区切られ、小数点としてピリオドを使用して入力する必要があります。

グループ化されたデータの平均偏差

間隔にグループ化されたデータの平均偏差を計算するには、次の手順に従う必要があります。

統計データセットの算術平均を求めます。データはグループ化されているため、平均を計算する式は次のようになります。

$\overline{x}=\cfrac{\sum_{i=1}^N x_i\cdot f_i}{N}$

平均からの各区間の偏差を計算します。これは、クラスの成績と平均の差の絶対値に相当します。

$|x_i-\overline{x}|$

各間隔の偏差にその絶対周波数を掛けます。

$|x_i-\overline{x}|\cdot f_i$

前のステップの結果をすべて合計し、データの総数で割ります。得られる結果は、間隔ごとにグループ化されたサンプルの平均偏差です。

$\cfrac{\sum_{i=1}^N|x_i-\overline{x}|\cdot f_i}{N}$

結論として、グループ化されたデータから平均偏差を取得する式は次のとおりです。

$D_{\overline{x}}=\cfrac{\sum_{i=1}^N|x_i-\overline{x}|\cdot f_i}{N}$

データがグループ化されるということは、通常、データが大量に存在することを意味し、平均偏差を見つけるには多くの手順が必要になります。したがって、通常は頻度表を使用して計算を実行します。

以下は、データが間隔にグループ化されている場合の平均偏差を計算する方法に関する段階的な演習です。

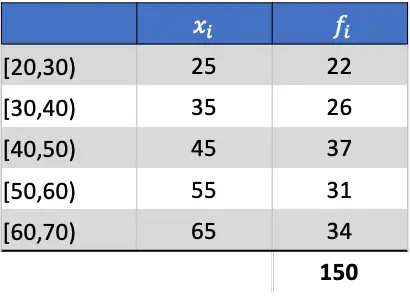
最初に行うことは、グループ化されたデータの平均を計算することです。これを行うには、クラスのメモに頻度を乗算してテーブルに列を追加します。

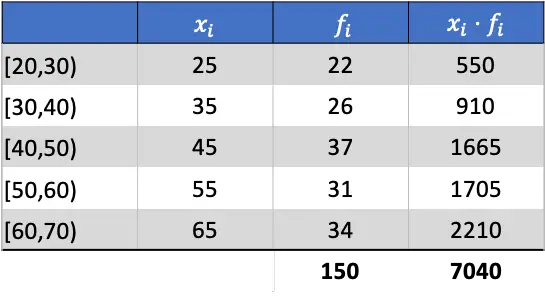
したがって、算術平均は、追加された列の合計を絶対度数の合計で除算した結果になります。

$\overline{x}=\cfrac{\sum_{i=1}^N x_i\cdot f_i}{N}=\cfrac{7040}{150}=46,93$

データの平均がわかったので、必要な列をすべて追加して平均偏差を求めることができます。

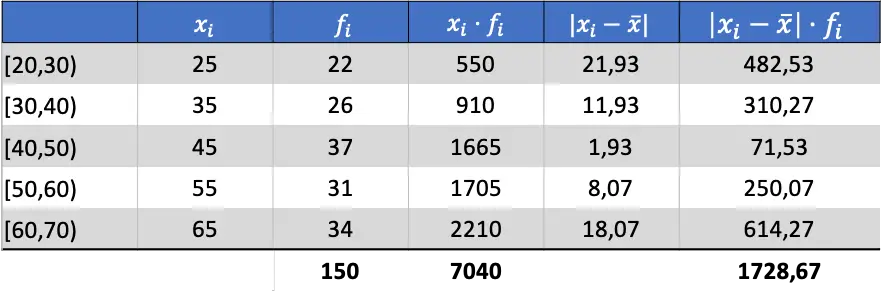
したがって、平均偏差を取得するには、最後の列の合計を観測値の合計数で割る必要があります。

$D_{\overline{x}}=\cfrac{\sum_{i=1}^N|x_i-\overline{x}|\cdot f_i}{N}=\cfrac{1728,67}{150}=11,52$

著者について

ベンジャミン・アンダーソン博士

私はベンジャミンです。退職した統計教授から、専任の Statorials 教育者になりました。統計分野における豊富な経験と専門知識を活かして、私は Statorials を通じて学生に力を与えるために自分の知識を共有することに尽力しています。もっと知る