事後確率: 定義 + 例

事後確率は、新しい情報を考慮した後にイベントが発生する更新された確率です。

たとえば、発生したばかりのイベント「B」を考慮した後にイベント「A」が発生する確率に興味があるかもしれません。この事後確率は次の式を使用して計算できます。

P(A|B) = P(A) * P(B|A) / P(B)

金：

P(A|B) = イベント B が発生した場合に、イベント A が発生する確率。 「|」に注意してください。 » は「与えられた」という意味です。

P(A) = イベント A が発生する確率。

P(B) = イベント B が発生する確率。

P(B|A) = イベント A が発生した場合に、イベント B が発生する確率。

例: 事後確率の計算

森林は 20% のオークと 80% のカエデで構成されています。オークの木の 90% は健全で、カエデの木は 50% だけが健全であることがわかっているとします。遠くから見て、特定の木が健康であることがわかるとします。その木がオークである確率はどれくらいですか?

イベント B が発生した場合にイベント A が発生する確率は次のとおりであることを思い出してください。

P(A|B) = P(A) * P(B|A) / P(B)

この例では、木が健康であるとすると、その木がオークである確率は次のようになります。

P(オーク|健全) = P(オーク) * P(健全|オーク) / P(健全)

P(オーク) = 森林内のすべての木の 20% がオークであるため、特定の木がオークである確率は0.2です。

P(健全) = 特定の木が健全である確率は次のように計算できます: (0.20)*(0.9) + (0.8)*(0.5) = 0.58 。

P(Healthy|Oak) = オークの 90% が健康であると言われているため、その木がオークであると仮定した場合、その木が健康である確率は0.9です。

これら 3 つの数値を使用すると、木が健康である場合に、その木がオークである確率がわかります。

P(オーク|健康) = P(オーク) * P(健康|オーク) / P(健康) = (0.2) * (0.9) / (0.58) = 0.3103 。

この確率を直感的に理解するために、次のグリッドがこの 100 本の木の森を表すと仮定しましょう。ちょうど 20 本の木がオークの木で、そのうち 18 本は健康です。残りの 80 本はカエデで、そのうち 40 本は健康です。

(O = オーク、M = メープル、緑 = 健康、赤 = 不健康)

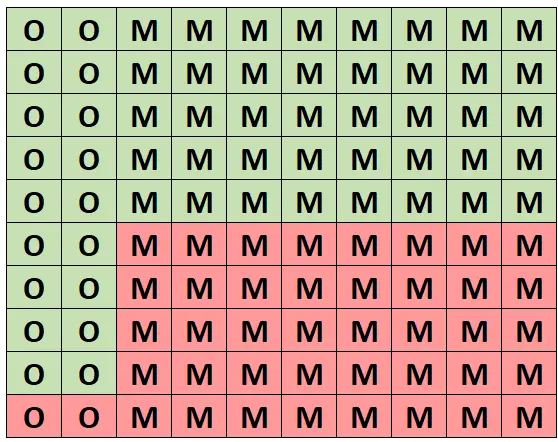
すべての木のうち、ちょうど 58 本が健全で、そのうち 18 本がオークです。したがって、健康な木を選択したことがわかっている場合、それがオークである確率は 18/58 = 0.3103となります。

事後確率はどのような場合に使用する必要がありますか?

事後確率は、金融、医学、経済学、天気予報など、幅広い分野で使用されています。

事後確率を使用するポイントは、新しい情報を入手したときに、何かについて持っていた以前の信念を更新することです。

前の例で、森の中の特定の木がオークである確率が 20% であることがわかったことを思い出してください。これは事前確率と呼ばれます。単純に木をランダムに選択した場合、それがオークである確率は 0.20 であることがわかりました。

ただし、選択した木が健全であるという新しい情報を取得すると、この新しい情報を使用して、この木がオークであることの事後確率が0.3103 であると判断できました。

現実の世界では、人々は常に新しい情報を発見しています。この新しい情報は、私たちが以前の信念を更新するのに役立ちます。統計用語では、これは、私たちが発生する出来事の事後確率を生成できることを意味します。これにより、世界をより正確に理解し、将来の出来事についてより正確に予測できるようになります。