二元配置分散分析: 定義、公式、および例

二元配置 ANOVA (「分散分析」) は、2 つの変数 (「因子」と呼ばれることもあります) に割り当てられた 3 つ以上の独立したグループの平均間に統計的に有意な差があるかどうかを判断するために使用されます。

このチュートリアルでは次について説明します。

• 二元配置分散分析を使用する場合。
• 二元配置分散分析を実行するために満たさなければならない仮定。
• 二元配置分散分析を実行する方法の例。

二元配置分散分析を使用する場合

2 つの因子が応答変数にどのような影響を与えるか、および応答変数に対する 2 つの因子間に交互作用効果があるかどうかを知りたい場合は、二元配置分散分析を使用する必要があります。

たとえば、植物学者が、日光への曝露と水やりの頻度が植物の成長にどのような影響を与えるかを調査したいとします。彼女は 40 個の種を植え、日光への曝露や水やりの頻度などのさまざまな条件で 2 か月間成長させます。 2 か月後、彼女は各植物の高さを記録します。

この場合、次の変数があります。

• 応答変数:植物の成長
• 要因:日光への曝露、水やりの頻度

そして、次の質問に答えたいと思います。

• 日光への曝露は植物の成長に影響しますか?
• 水やりの頻度は植物の成長に影響しますか？
• 日光への曝露と水やりの頻度の間に相互作用効果はありますか? （例えば、植物への日光曝露の影響は水やりの頻度によって異なります）

2 つの因子があるため、この分析には二元配置分散分析を使用します。代わりに、水やりの頻度だけが植物の成長にどの程度影響するかを知りたい場合は、1 つの因子のみを扱うため、一元配置分散分析を使用します。

二元配置分散分析の仮定

二元配置 ANOVA の結果が有効であるためには、次の前提を満たす必要があります。

1. 正規性– 応答変数は各グループに対してほぼ正規分布します。

2. 分散が等しい– 各グループの分散はほぼ等しい必要があります。

3. 独立性– 各グループ内の観測値は互いに独立しており、グループ内の観測値はランダムサンプリングによって取得されました。

二元配置分散分析: 例

植物学者は、植物の成長が日光への曝露や水やりの頻度によって影響を受けるかどうかを知りたいと考えています。彼女は 40 個の種を植え、日光への曝露や水やりの頻度などのさまざまな条件で 2 か月間成長させます。 2 か月後、彼女は各植物の高さを記録します。結果を以下に示します。

上の表では、各条件の組み合わせで 5 つの植物が栽培されたことがわかります。

たとえば、5 つの植物を毎日水やり、日光を当てずに育てたところ、2 か月後の高さは 4.8 インチ、4.4 インチ、3.2 インチ、3.9 インチ、4.4 インチでした。

Excel で二元配置分散分析を実行し、次の結果が得られます。

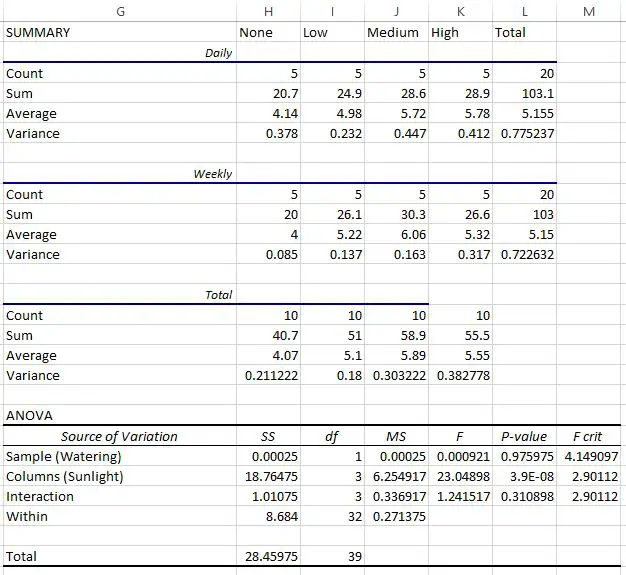
最後の表は、二元配置分散分析の結果を示しています。次のことが観察できます。

• 水やりの頻度と日光への曝露の間の相互作用の p 値は0.310898でした。これは、0.05 アルファ レベルでは統計的に有意ではありません。
• 水やり頻度の p 値は0.975975でした。これは、0.05 アルファ レベルでは統計的に有意ではありません。
• 日光曝露の p 値は3.9E-8 (0.000000039)でした。これは、アルファ レベル 0.05 で統計的に有意です。

これらの結果は、日光への曝露が草丈に統計的に有意な影響を与える唯一の要因であることを示しています。

また、相互作用効果がないため、日光曝露の影響は水やり頻度の各レベルで一貫しています。

簡単に言えば、植物に毎日水やりをするか毎週水をやるかは、日光への曝露が植物に与える影響には影響しません。

追加リソース

次の記事では、さまざまな統計ソフトウェアを使用して二元配置分散分析を実行する方法について説明します。

Excel で二元配置分散分析を実行する方法
R で二元配置分散分析を実行する方法
Python で二元配置分散分析を実行する方法
SPSS で二元配置分散分析を実行する方法
Stata で二元配置分散分析を実行する方法