Python で二次回帰を実行する方法
二次回帰は、真の関係が二次である場合に、予測子変数と応答変数の間の関係を定量化するために使用できる回帰の一種であり、グラフ上の「U」または反転した「U」のように見える場合があります。
つまり、予測変数が増加すると、応答変数も増加する傾向がありますが、ある点を超えると、予測変数が増加し続けるため、応答変数は減少し始めます。
このチュートリアルでは、Python で二次回帰を実行する方法について説明します。
例: Python での二次回帰
16 人の異なる人々について、週あたりの労働時間数と報告された幸福度 (0 ~ 100 のスケール) に関するデータがあるとします。
import numpy as np import scipy.stats as stats #define variables hours = [6, 9, 12, 12, 15, 21, 24, 24, 27, 30, 36, 39, 45, 48, 57, 60] happ = [12, 18, 30, 42, 48, 78, 90, 96, 96, 90, 84, 78, 66, 54, 36, 24]
このデータの単純な散布図を作成すると、2 つの変数間の関係が「U」字型であることがわかります。
import matplotlib.pyplot as plt
#create scatterplot
plt.scatter(hours, happ)
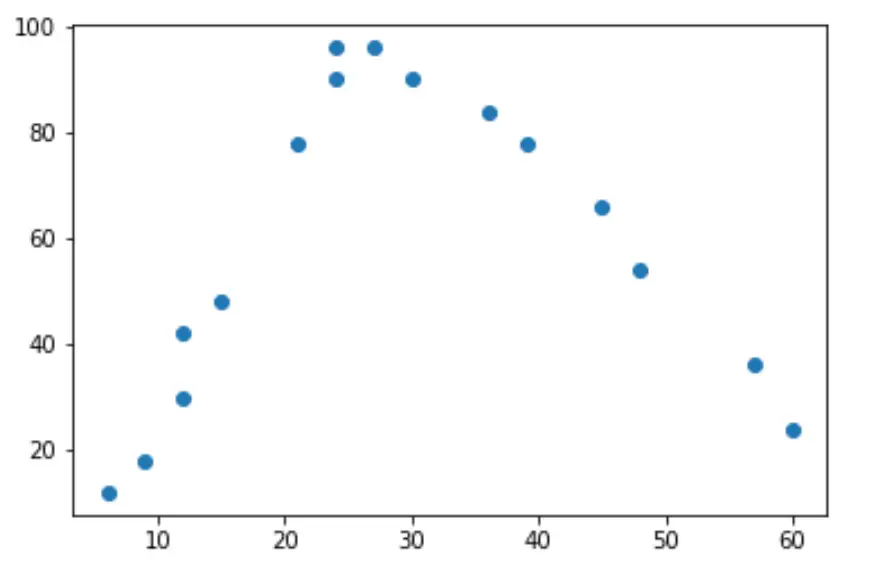
労働時間が増加すると幸福度も増加しますが、労働時間が週あたり約 35 時間を超えると幸福度は減少し始めます。
この「U」字型のため、2 次回帰が 2 つの変数間の関係を定量化するための適切な候補である可能性が高いことを意味します。
実際に二次回帰を実行するには、 numpy.polyfit()関数を使用して次数 2 の多項式回帰モデルを近似します。
import numpy as np #polynomial fit with degree = 2 model = np.poly1d(np.polyfit(hours, happ, 2)) #add fitted polynomial line to scatterplot polyline = np.linspace(1, 60, 50) plt.scatter(hours, happ) plt.plot(polyline, model(polyline)) plt.show()
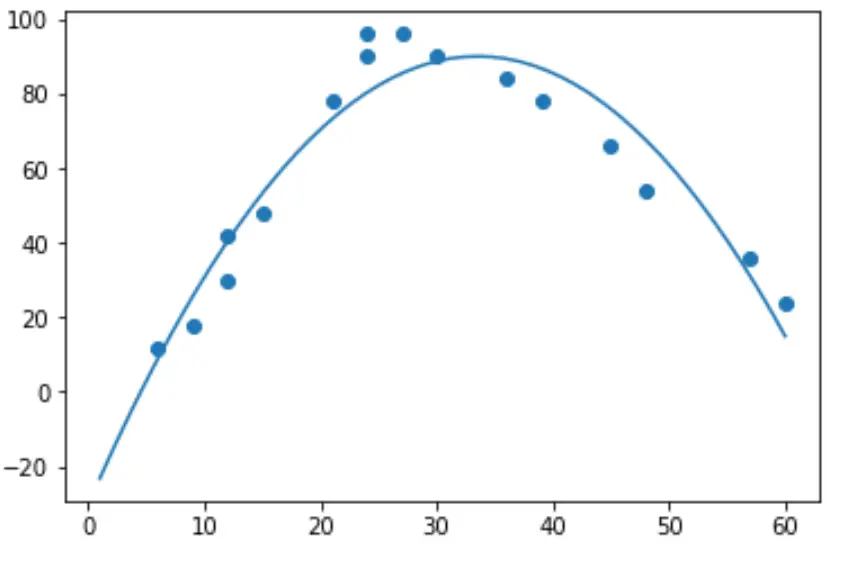
モデル係数を出力することで、近似された多項式回帰方程式を取得できます。
print (model)
-0.107x 2 + 7.173x - 30.25
近似された二次回帰式は次のとおりです。
幸福度 = -0.107(時間) 2 + 7.173(時間) – 30.25
この方程式を使用して、労働時間に基づいて個人の期待される幸福度を計算できます。たとえば、週に 30 時間働く人の期待される幸福度は次のとおりです。
幸福度 = -0.107(30) 2 + 7.173(30) – 30.25 = 88.64 。
モデルの R 二乗 (予測子変数によって説明できる応答変数の分散の割合) を取得する短い関数を作成することもできます。
#define function to calculate r-squared def polyfit(x, y, degree): results = {} coeffs = np.polyfit(x, y, degree) p = np.poly1d(coeffs) #calculate r-squared yhat = p(x) ybar = np.sum(y)/len(y) ssreg = np.sum((yhat-ybar)**2) sstot = np.sum((y - ybar)**2) results['r_squared'] = ssreg / sstot return results #find r-squared of polynomial model with degree = 3 polyfit(hours, happ, 2) {'r_squared': 0.9092114182131691}
この例では、モデルの R 二乗は0.9092です。
これは、報告された幸福度の変動の 90.92% が予測変数によって説明できることを意味します。