紛らわしい変数とは何ですか? (定義&例)
どのような実験においても、次の 2 つの主要な変数があります。
独立変数:従属変数への影響を観察できるようにするために、実験者が変更または制御する変数。
従属変数:独立変数に「依存する」実験で測定される変数。

研究者は多くの場合、独立変数の変化が従属変数にどのような影響を与えるかを理解することに関心を持っています。
ただし、場合によっては 3 番目の変数が考慮されず、調査対象の 2 つの変数間の関係に影響を与える可能性があります。
このタイプの変数は交絡変数として知られており、研究結果を混乱させ、実際には存在しない 2 つの変数間にある種の因果関係があるかのように見せる可能性があります。
交絡変数:実験には含まれないが、実験内の 2 つの変数間の関係に影響を与える変数。
このタイプの変数は実験の結果を混乱させ、信頼性の低い結果につながる可能性があります。
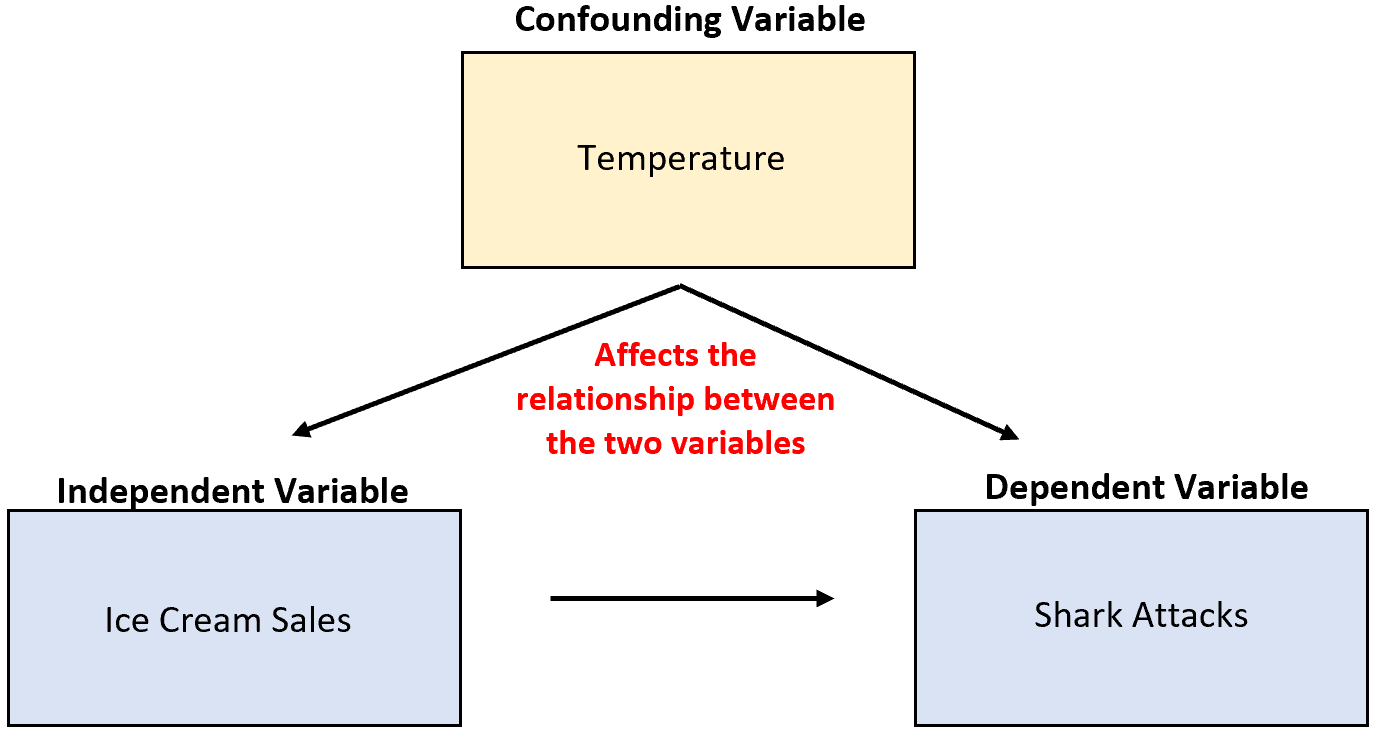
たとえば、研究者がアイスクリームの販売とサメの襲撃に関するデータを収集し、2 つの変数に高い相関があることを発見したとします。これは、アイスクリームの売上の増加がサメの襲撃を引き起こしていることを意味するのでしょうか?
それはありそうにありません。最も考えられる原因は、紛らわしい温度変数です。外が暖かくなると、アイスクリームを買う人も海に行く人も増えます。
紛らわしい変数の要件
変数が紛らわしい変数であるためには、次の要件を満たしている必要があります。
1. 独立変数と相関している必要があります。
前の例では、気温はアイスクリームの売上の独立変数と相関していました。特に、気温が高いとアイスクリームの売上が増加し、気温が低いと売上が減少します。
2. 従属変数との因果関係がなければなりません。
前の例では、温度はサメの攻撃の数に直接的な因果関係を持っていました。特に、気温が上昇すると海に入る人が増え、サメに襲われる可能性が直接的に高まります。
混乱を招く変数がなぜ問題となるのでしょうか?
交絡変数は次の 2 つの理由で問題になります。
1. 交絡変数により、因果関係が実際には存在しないにもかかわらず、存在するように見えることがあります。
前の例では、温度という紛らわしい変数により、アイスクリームの売り上げとサメの攻撃の間に因果関係があるかのように見えました。
しかし、アイスクリームの販売がサメの襲撃を引き起こすわけではないことはわかっています。温度という紛らわしい変数がそのように思わせます。
2. 交絡変数により、変数間の真の因果関係が曖昧になる可能性があります。
血圧を下げる運動の能力を研究しているとします。交絡変数となる可能性があるのは開始時の体重で、これは運動と相関関係があり、血圧に直接的な因果関係を持ちます。
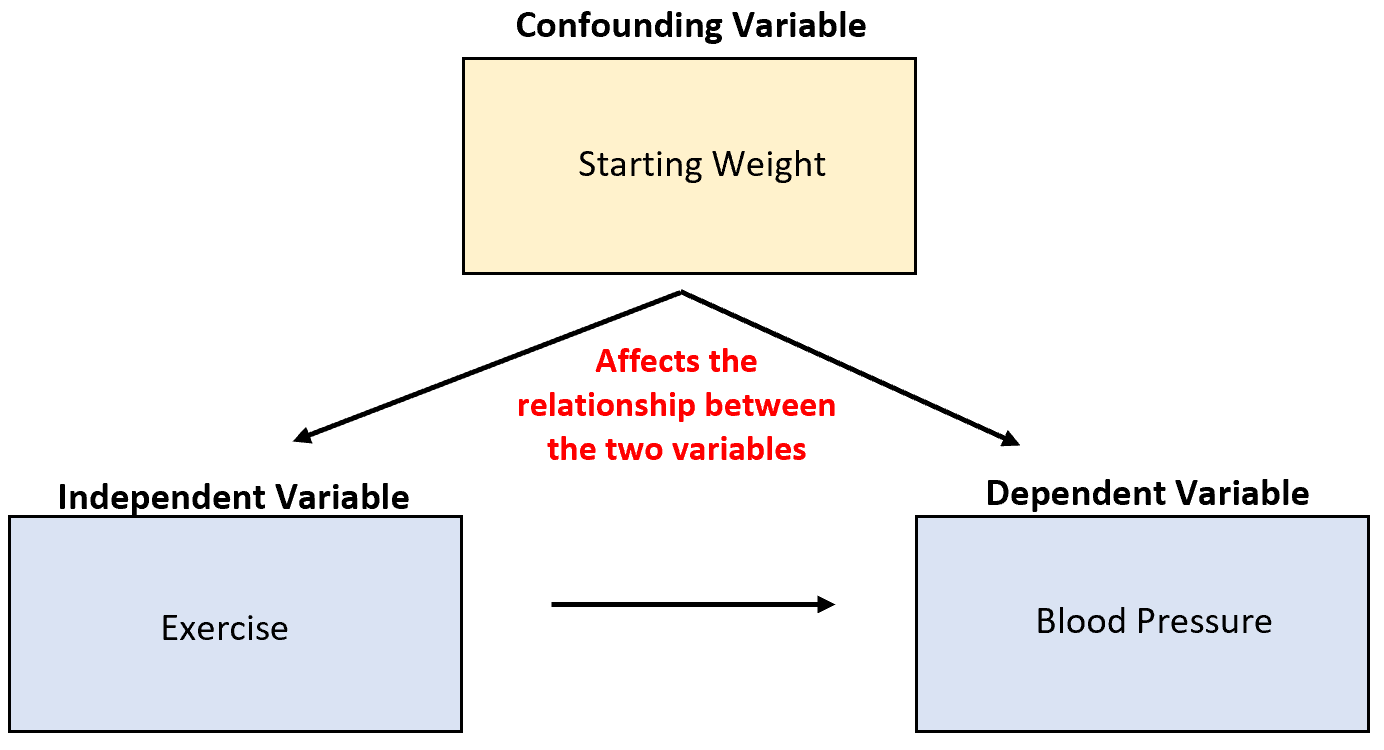
身体活動の増加は血圧の低下につながる可能性がありますが、個人の開始体重もこれら 2 つの変数間の関係に大きな影響を与えます。
交絡変数と内部妥当性
専門用語で言えば、交絡変数は研究の内部妥当性、つまり従属変数の変化が独立変数の変化に帰属することの妥当性に影響を与えます。
交絡変数が存在する場合、従属変数で観察される変化が独立変数の変化の直接の結果であると常に確信を持って言うことができません。
混乱を招く変数の影響を軽減する方法
混乱を招く変数の影響を軽減するには、次のような方法がいくつかあります。
1. ランダム割り当て
ランダム割り当てとは、研究内の個人を治療グループまたは対照グループにランダムに割り当てるプロセスを指します。
たとえば、新しい錠剤の血圧に対する影響を研究したいとします。研究に参加する人を 100 人募集した場合、乱数発生器を使用して、50 人を対照グループ (錠剤なし) にランダムに割り当て、50 人を治療グループ (新しい錠剤) に割り当てることができます。
ランダムな割り当てを使用することにより、2 つのグループがほぼ同様の特性を持つ可能性が高まります。これは、2 つのグループ間で観察された差異が治療に起因する可能性があることを意味します。
これは、研究には内部的妥当性がなければならないことを意味します。つまり、グループ間の血圧の差異を、グループ内の個人間の差異ではなく、錠剤自体のせいとするのは正当であるということです。
2. ブロッキング
ブロッキングとは、交絡変数の影響を排除するために、交絡変数の特定の値に基づいて研究内の個人を「ブロック」に分割する手法を指します。
たとえば、研究者が体重減少に対する新しい食事の影響を理解したいと考えているとします。独立変数は新しい食事、従属変数は体重減少量です。
ただし、体重減少の変動を引き起こす可能性のある交絡変数の 1 つは性別です。新しいダイエットが効果があるかどうかにかかわらず、個人の性別が体重の減少量に影響を与える可能性があります。
この問題を解決する 1 つの方法は、個人を 2 つのブロックのいずれかに配置することです。
- 男
- 女性
次に、各ブロック内で個人を次の 2 つの治療法のいずれかにランダムに割り当てます。
- 新しいダイエット
- 標準的な食事
こうすることで、各ブロック内の変動はすべての個人間の変動よりもはるかに小さくなり、性別をコントロールしながら新しい食事が減量にどのような影響を与えるかをよりよく理解できるようになります。
3. 対応
マッチドペア計画は、潜在的な交絡変数の値に基づいて個人を「照合」する実験計画の一種です。
たとえば、研究者が、標準的な食事と比較して、新しい食事が体重減少にどのような影響を与えるかを知りたいと考えているとします。この状況で紛らわしい可能性がある 2 つの変数は、年齢と性別です。
これを考慮して、研究者から 100 人の被験者を募集し、年齢と性別に基づいて 50 組にグループ化します。例えば:
- 25 歳の男性は、年齢と性別の点で「一致」するため、別の 25 歳の男性とマッチングされます。
- 30歳の女性は、年齢や性別などの点でも一致するため、別の30歳の女性とマッチングされます。
次に、各ペア内で、1 人の被験者が 30 日間新しい食事療法に従うようにランダムに割り当てられ、もう 1 人の被験者が 30 日間標準的な食事療法に従うように割り当てられます。
30 日間の終わりに、研究者は各被験者の総体重減少を測定します。
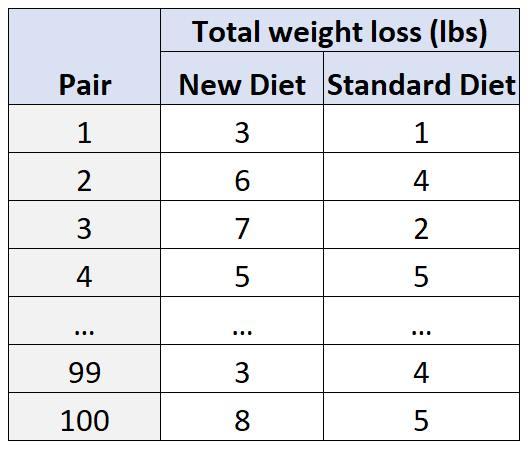
このタイプの設計を使用することにより、研究者は、体重減少の差異が、年齢や性別という交絡変数ではなく、使用された食事の種類に起因していることを確信できます。
このタイプの設計には、次のようないくつかの欠点があります。
1. 1 人が脱落した場合、2 人の被験者を失います。被験者が研究から脱落することを決めた場合、完全なペアはもう存在しないため、実際には 2 人の被験者を失うことになります。
2. 一致するものを見つけるのに時間がかかります。性別や年齢など、特定の変数に一致するトピックを見つけるには時間がかかる場合があります。
3. トピックを完全に一致させることができません。どれだけ努力しても、各ペアの主題には常にばらつきが生じます。
ただし、研究にこの設計を実装するために利用できるリソースがある場合、交絡変数の影響を排除するのに非常に効果的です。