F 分布を使用して信頼区間を作成する方法
2 つの母集団の分散が等しいかどうかを判断するには、分散比σ 2 1 / σ 2 2を計算できます。ここで、σ 2 1は母集団 1 の分散、σ 2 2は母集団 2 の分散です。
真の母集団分散比を推定するには、通常、各母集団から 単純な無作為サンプルを取得し、サンプル分散比s 1 2 / s 2 2を計算します。ここで、s 1 2と s 2 2はサンプル 1 とサンプルのサンプル分散です。 。それぞれ2。
この検定は、s 1 2と s 2 2 が、どちらも正規分布母集団からのサイズ n 1と n 2の独立したサンプルから計算されることを前提としています。
この比率が 1 から遠ざかるほど、母集団内の分散が不均等である証拠が強くなります。
σ 2 1 / σ 2 2の(1-α)100% 信頼区間は次のように定義されます。
(s 1 2 / s 2 2 ) * F n 1 -1, n 2 -1, α/2 ≤ σ 2 1 / σ 2 2 ≤ (s 1 2 / s 2 2 ) * F n 2 -1, n 1 -1、 α/2
ここで、F n 2 -1、n 1 -1、α/2および F n 1 -1、n 2 -1、 α/2 は、選択された有意水準 α に対する分布 F の臨界値です。
次の例は、3 つの異なる方法を使用して σ 2 1 / σ 2 2の信頼区間を作成する方法を示しています。
- 手によって
- Microsoft Excelを使用する
- R統計ソフトの利用
次の各例では、次の情報を使用します。
- α = 0.05
- n 1 = 16
- n2 = 11
- s 1 2 =28.2
- s 2 2 = 19.3
信頼区間を手動で作成する
σ 2 1 / σ 2 2の信頼区間を手動で計算するには、得た数値を信頼区間の式に代入するだけです。
(s 1 2 / s 2 2 ) * F n1-1, n2-1,α/2 ≤ σ 2 1 / σ 2 2 ≤ (s 1 2 / s 2 2 ) * F n2-1, n1-1, α/2
欠落している数値は臨界値だけです。幸いなことに、分布テーブル Fでこれらの重要な値を見つけることができます。
F n2-1、n1-1、α/2 = F 10、15、0.025 = 3.0602
F n1-1、n2-1、 α/2 = 1/F 15、10、0.025 = 1 / 3.5217 = 0.2839
(クリックすると表が拡大されます)
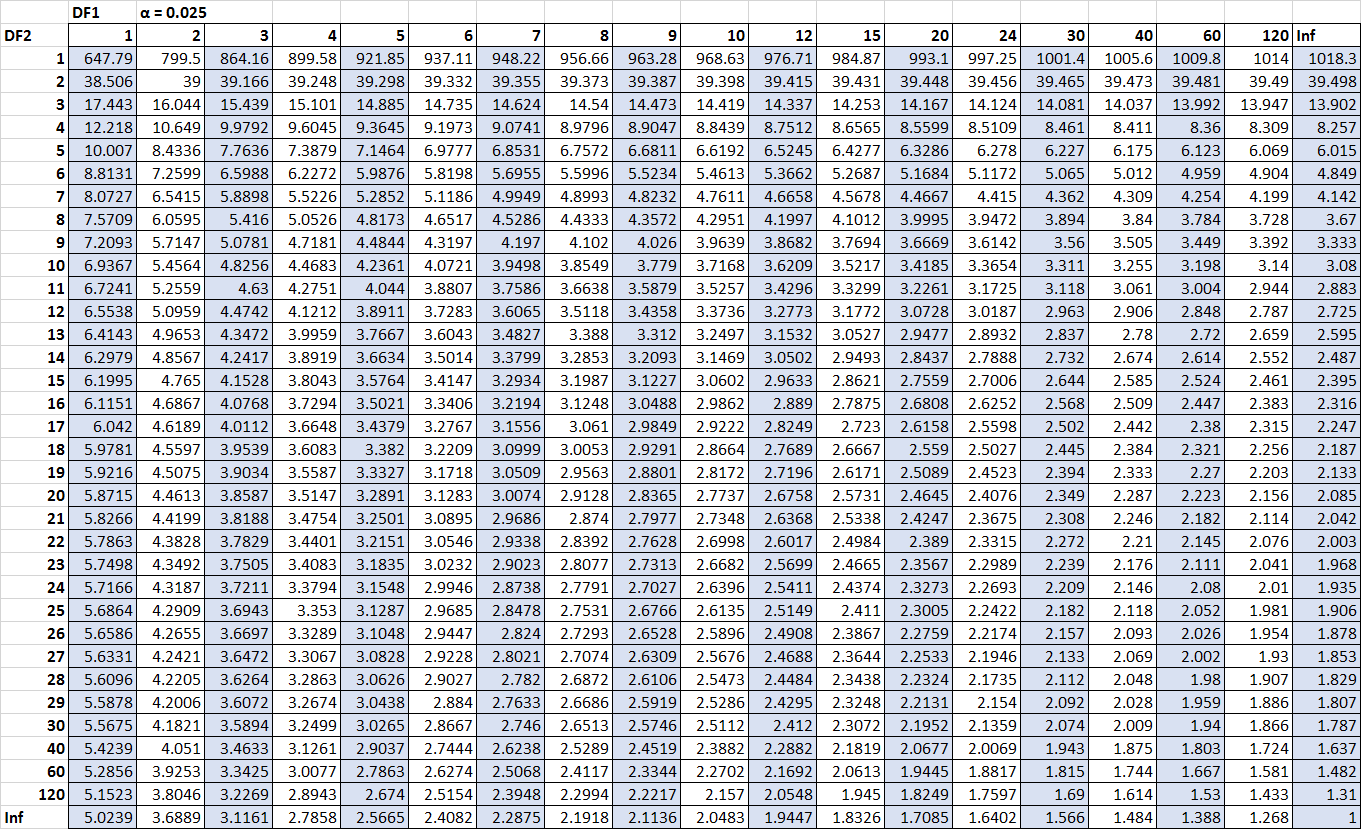
これで、すべての数値を信頼式区間に代入できます。
(s 1 2 / s 2 2 ) * F n1-1, n2-1,α/2 ≤ σ 2 1 / σ 2 2 ≤ (s 1 2 / s 2 2 ) * F n2-1, n1-1, α/2
(28.2 / 19.3) * (0.2839) ≤ σ 2 1 / σ 2 2 ≤ (28.2 / 19.3) * (3.0602)
0.4148 ≤ σ 2 1 / σ 2 2 ≤ 4.4714
したがって、母集団分散比の 95% 信頼区間は(0.4148, 4.4714)となります。
Excel を使用した信頼区間の作成
次の図は、Excel で母集団分散比の 95% 信頼区間を計算する方法を示しています。信頼区間の下限と上限は列 E に示され、下限と上限を求めるために使用される式は列 F に示されます。
したがって、母集団分散比の 95% 信頼区間は(0.4148, 4.4714)となります。これは、信頼区間を手動で計算したときに得られた値と一致します。
R を使用した信頼区間の作成
次のコードは、R の母集団分散比の 95% 信頼区間を計算する方法を示しています。
#define significance level, sample sizes, and sample variances alpha <- .05 n1 <- 16 n2 <- 11 var1 <- 28.2 var2 <- 19.3 #define F critical values upper_crit <- 1/qf(alpha/2, n1-1, n2-1) lower_crit <- qf(alpha/2, n2-1, n1-1) #find confidence interval lower_bound <- (var1/var2) * lower_crit upper_bound <- (var1/var2) * upper_crit #output confidence interval paste0("(", lower_bound, ", ", upper_bound, " )") #[1] "(0.414899337980266, 4.47137571035219 )"
したがって、母集団分散比の 95% 信頼区間は(0.4148, 4.4714)となります。これは、信頼区間を手動で計算したときに得られた値と一致します。