分散
この記事では、分散とも呼ばれる分散とは何か、またその計算方法について説明します。分散の公式、分散計算の具体例が記載されており、さらにオンライン計算機を使用して任意のデータセットの分散を計算することができます。
また、グループ化されたデータの分散を別の方法で見つける方法も示します。最後に、母集団の分散と標本分散の違い、分散と標準偏差の違い、およびこの統計的尺度の特性について説明します。
分散とは何ですか?
統計学における分散は、確率変数の変動性を示す分散の尺度です。分散は、残差の二乗和を観測値の総数で割ったものに等しくなります。
残差は、統計データ ポイントの値とデータ セットの平均の差として理解されることに注意してください。
確率論では、分散の記号はギリシャ文字のシグマ二乗 (σ 2 ) です。通常はVar(X)としても表されますが、 X は分散の計算元となる確率変数です。
一般に、確率変数の分散値の解釈は簡単です。分散値が大きいほど、データはより分散しています。逆も同様で、分散値が小さいほど、データ系列の分散は少なくなります。ただし、分散を解釈するときは、外れ値によって分散値が歪められる可能性があるため、外れ値に注意する必要があります。
分散、分散以外に考慮される他の尺度には、範囲、標準偏差、平均偏差、および変動係数があります。
ギャップの計算方法
分散を計算するには、次の手順を実行する必要があります。
- データセットの算術平均を求めます。
- データセットの値と平均の差として定義される残差を計算します。
- 各余りを二乗します。
- 前のステップで計算されたすべての結果を加算します。
- データの総数で割ります。得られる結果は、データ系列の分散です。
結論として、データセットの分散を計算する式は次のとおりです。

金:
-

分散を計算する確率変数です。
-

データ値です

。
-

観測値の合計数です。
-

確率変数の平均です

。
👉以下の計算機を使用して、任意のデータセットの分散を計算できます。
したがって、データ系列から分散を抽出するには、算術平均の計算方法を理解しておくことが不可欠です。これを行う方法を覚えていない場合は、上記のリンク先の記事で確認してください。
偏差の例
分散の定義がわかったので、データ系列の分散がどのように取得されるかを確認できるように、段階的に演習を解いていきます。
- 多国籍企業の過去 5 年間の経済的成果は知られており、大部分は利益を得ましたが、ある年には 1,150 万、2、9、700 万ユーロという多大な損失を出しました。このデータセットの分散を計算します。
上の説明で見たように、データ系列の分散を見つけるために最初に行う必要があるのは、その算術平均を計算することです。
![]()
データの平均値がわかったら、分散の公式を使用できます。

演習ステートメントで提供されるデータを式に代入します。
![]()
最後に、残っているのは、分散を計算するための演算を解くことだけです。
![Rendered by QuickLaTeX.com \begin{aligned}Var(X)&=\cfrac{7,8^2+1,8^2+(-1,2)^2+(-12,2)^2+3,8^2}{5}\\[2ex]&=\cfrac{60,84+3,24+1,44+148,84+14,44}{5}\\[2ex]&= \cfrac{228,8}{5} \\[2ex]&=45,76 \ \text{millones de euros}^2\end{aligned}](https://statorials.org/wp-content/ql-cache/quicklatex.com-c2cbee60d77f19e88117e1bcf28d9cb2_l3.png)
分散単位は統計データの単位と同じですが二乗されていることに注意してください。このため、このデータ グループの分散は 4,576 万ユーロ2です。
ギャップ計算機
次の計算機に統計データ セットを入力して、その分散を計算します。データはスペースで区切られ、小数点としてピリオドを使用して入力する必要があります。
グループ化されたデータの分散
間隔 にグループ化されたデータの分散を計算するには、次の手順に従う必要があります。
- グループ化されたデータの平均を求めます。
- グループ化されたデータの残差を計算します。
- 各余りを二乗します。
- 以前の各結果にその間隔の頻度を掛けます。
- 前のステップで取得したすべての値の合計を加算します。
- 観測値の合計数で割ります。結果として得られる数値は、グループ化されたデータの分散です。
つまり、間隔にグループ化されたデータの分散を計算する式は次のようになります。
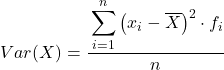
通常は上記の式が使用されますが、以下の代数式も同等であるため使用できます。
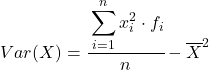
例として、次のグループ化されたデータ系列の分散を求めます。
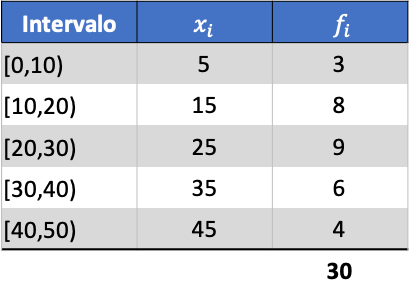
まず、グループ化されたデータの平均を決定する必要があります。これを行うには、クラスマークと頻度の積を含む列を頻度テーブルに追加します。
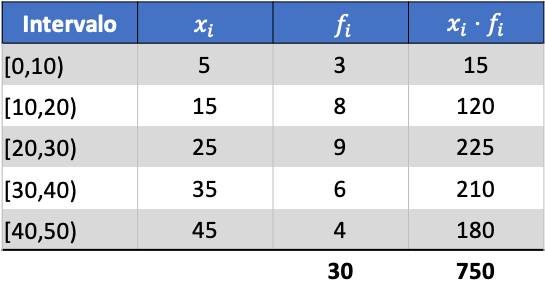
ここで、追加した列の合計をデータの総数で割ることにより、グループ化されたデータの平均を計算します。
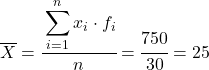
そして、計算されたデータの平均から、次の 3 つの列を追加できます。
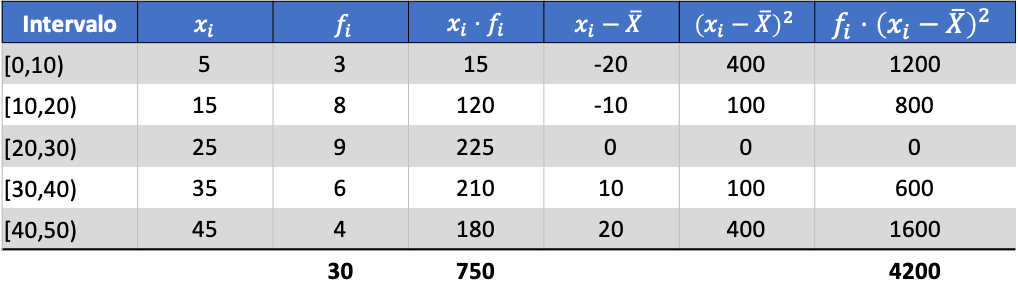
したがって、プールされたデータセットの分散は、最後の列の合計を観測データの総数で割ったものになります。
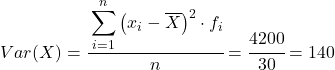
分散と標準偏差
分散と標準偏差 (または標準偏差) は分散の 2 つの尺度であり、どちらもデータセットの分散の度合いを示します。ただし、分散と標準偏差の違いは、一般に分散の方が標準偏差の 2 乗であるため、値が大きくなるということです。
標準偏差は一般にギリシャ文字のシグマ (σ) で表され、分散はこれら 2 つの分散メトリックの間に存在する数学的関係であるため、分散は文字シグマの二乗 (σ 2 ) で表されます。
![]()
したがって、データ セットの分散値を計算したら、分散の平方根を求めるだけで、同じセットの標準偏差値を簡単に見つけることができます。
![]()
母集団分散と標本分散
論理的には、母集団の分散は統計的な母集団の分散の計算を指しますが、代わりに標本の分散が標本の分散の計算に適用されます。ただし、母集団分散の式は標本分散の式とは異なるため、これらは 2 つの異なる概念です。
通常、分散の演習では、特に指示がない限り、提供されたデータセットの分散を求めるには、母分散の式を使用する必要があります。これは、記事の冒頭で説明したものです。
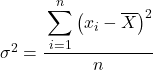
しかし、おそらく一部の問題では、統計データを標本として扱うように求められます。その場合、標本分散の式を使用する必要があります。
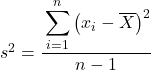
母集団分散が計算されていることを示すにはギリシャ文字 σ で示されますが、標本分散が計算される場合には文字 s が使用されることに注意してください。
ご覧のとおり、2 つの式の唯一の違いは、サンプルの分散を観測値の総数から 1 を引いた値で割る必要があることです。たとえば、データ項目が合計 30 個ある場合、29 で割ります。ただし、分子の計算はまったく同じ方法で行われます。
分散特性
分散には次の特性があります。
- ランダム変数の分散は常に 0 以上になります。同様に、分散がゼロの場合、すべての統計データが同じであることを意味します。
![]()
- 明らかに、単一値の分散はゼロです。
![]()
- スカラーと変数の積の分散は、そのスカラーの 2 乗と変数の分散の積に相当します。
![]()
- 2 つの従属変数の合計の分散は、各変数の個別の分散の合計に 2 つの変数間の共分散の 2 倍を加えたものに相当します。
![]()
- したがって、2 つの変数が独立している場合、それらの合計の分散を求めるには、それらの分散を加算するだけで十分です。
![]()
- 偏差は、次の式を使用して数学的期待値で定義することもできます。
![]()