R の加重標準偏差を計算する方法
加重標準偏差は、データセット内の一部の値の重みが他の値よりも高い場合に、データセット内の値の分散を測定するのに便利な方法です。
加重標準偏差を計算する式は次のとおりです。
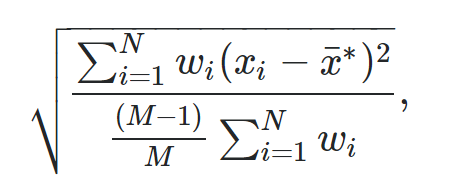
金:
- N:観測値の総数
- M:ゼロ以外の重みの数
- w i :重みベクトル
- x i :データ値のベクトル
- x :加重平均
R で加重標準偏差を計算する最も簡単な方法は、 Hmiscパッケージのwt.var()関数を使用することです。この関数は次の構文を使用します。
#define data values x <- c(4, 7, 12, 13, ...) #define weights wt <- c(.5, 1, 2, 2, ...) #calculate weighted variance weighted_var <- wtd. var (x, wt) #calculate weighted standard deviation weighted_sd <- sqrt(weighted_var)
次の例は、この関数を実際に使用する方法を示しています。
例 1: ベクトルの加重標準偏差
次のコードは、R の単一ベクトルの重み付き標準偏差を計算する方法を示しています。
library (Hmisc) #define data values x <- c(14, 19, 22, 25, 29, 31, 31, 38, 40, 41) #define weights wt <- c(1, 1, 1.5, 2, 2, 1.5, 1, 2, 3, 2) #calculate weighted variance weighted_var <- wtd. var (x, wt) #calculate weighted standard deviation sqrt(weighted_var) [1] 8.570051
加重標準偏差は8.57であることがわかります。
例 2: データ フレーム内の列の加重標準偏差
次のコードは、R のデータ フレームの列の重み付き標準偏差を計算する方法を示しています。
library (Hmisc) #define data frame df <- data. frame (team=c('A', 'A', 'A', 'A', 'A', 'B', 'B', 'C'), wins=c(2, 9, 11, 12, 15, 17, 18, 19), dots=c(1, 2, 2, 2, 3, 3, 3, 3)) #define weights wt <- c(1, 1, 1.5, 2, 2, 1.5, 1, 2) #calculate weighted standard deviation of points sqrt(wtd. var (df$points, wt)) [1] 0.6727938
ポイント列の加重標準偏差は0.673であることがわかります。
例 3: データ フレーム内の複数の列の加重標準偏差
次のコードは、R のsapply()関数を使用して、データ フレーム内の複数の列の加重標準偏差を計算する方法を示しています。
library (Hmisc) #define data frame df <- data. frame (team=c('A', 'A', 'A', 'A', 'A', 'B', 'B', 'C'), wins=c(2, 9, 11, 12, 15, 17, 18, 19), dots=c(1, 2, 2, 2, 3, 3, 3, 3)) #define weights wt <- c(1, 1, 1.5, 2, 2, 1.5, 1, 2) #calculate weighted standard deviation of points and wins sapply(df[c(' wins ', ' points ')], function(x) sqrt(wtd. var (x, wt))) win points 4.9535723 0.6727938
勝利列の加重標準偏差は4.954 、ポイント列の加重標準偏差は0.673です。