完全ガイド: 二元配置分散分析結果をレポートする方法
二元配置分散分析は、 2 つの変数に分割された 3 つ以上の独立したグループの平均間に統計的に有意な差があるかどうかを判断するために使用されます。
二元配置分散分析の結果を報告するときは、常に次の一般的な構造を使用します。
- 独立変数と従属変数の簡単な説明。
- 2 つの独立変数間に有意な交互作用効果があったかどうか。
- 2 つの独立変数が従属変数に統計的に有意な影響を与えたかどうか。
使用できる正確な表現は次のとおりです。
二元配置分散分析を実行して、[従属変数] に対する [独立変数 1] と [独立変数 2] の影響を分析しました。
二元配置分散分析により、[独立変数 1] と [独立変数 2] の効果の間に統計的に有意な相互作用があるかどうかが明らかになりました (F (df 相互作用、df 内) = [F 値]、p = [p-価値])。
簡単な手の効果分析により、[独立変数 1] が [従属変数] に対して統計的に有意な影響を[持っていた、または持っていなかった]ことが示されました (p = [p 値])。
単純な手の効果分析により、[独立変数 2] が [従属変数] に対して統計的に有意な影響を[持っていた、または持っていなかった] (p = [p 値]) ことが示されました。
次の例は、実際に二元配置分散分析の結果をレポートする方法を示しています。
例: 二元配置分散分析の結果のレポート
ある植物学者は、日光への曝露レベルや水やりの頻度の違いが植物の成長に影響を与えるかどうかを知りたいと考えています。彼女は 40 個の種を植え、日光への曝露や水やりの頻度などのさまざまな条件で 1 か月間成長させます。
次に、二元配置分散分析を実行して、日光への曝露と水やりの頻度が植物の成長に影響を与えるかどうかを判断します。
次の表は、二元配置分散分析の結果を示しています。
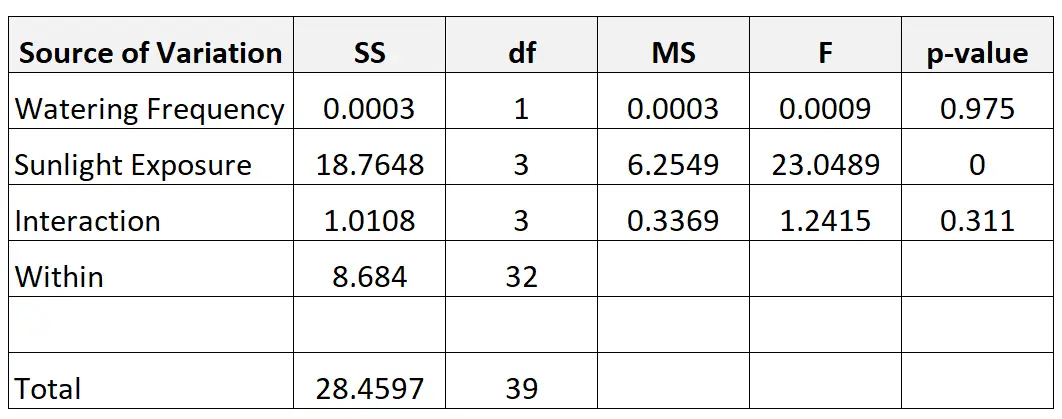
二元配置分散分析結果をレポートする方法は次のとおりです。
二元配置分散分析を実行して、水やりの頻度と日光への曝露が植物の成長に及ぼす影響を分析しました。
二元配置分散分析により、水やりの頻度と日光曝露の影響の間に統計的に有意な相互作用がないことが明らかになりました (F(3,32) = 1.242、p = 0.311)。
簡単な手の影響分析では、水やりの頻度が植物の成長に統計的に有意な影響を及ぼさないことが示されました (p = 0.975)。
簡単な手の影響分析により、太陽光への曝露が植物の成長に統計的に有意な影響を与えることが示されました (p < 0.000)。
留意すべき事項
二元配置 ANOVA の結果を提示する際に留意すべき点がいくつかあります。
1. 必要に応じて、記述統計テーブルを使用します。
- 読者にデータのより完全な全体像を与えるために、各治療グループの値の平均と標準偏差も示す記述統計の表を提示すると役立つ場合があります。
2. 必要に応じて p 値を丸めます。
- 通常、分散分析結果の全体の F 値とすべての p 値は、簡潔にするために小数点以下 2 桁または 3 桁に四捨五入されます。
- 使用する小数点以下の桁数に関係なく、レポート全体で一貫性を保ってください。
追加リソース
次のチュートリアルでは、APA 形式で他の統計テストと手順をレポートする方法について説明します。
一元配置分散分析結果をレポートする方法 (例付き)
クロンバックのアルファを報告する方法 (例付き)
t 検定結果を報告する方法: 例付き
ピアソン相関関係をレポートする方法: 例付き
回帰結果を報告する方法: 例付き