周波数ポリゴン
この記事では、周波数ポリゴンとは何か、またその用途について説明します。さらに、さまざまな種類の周波数ポリゴンとは何か、およびそれぞれの例についても学習します。
周波数ポリゴンとは何ですか?
周波数ポリゴンは、データセットが点で表され、線で接続された統計グラフの一種です。
統計では、時系列を表すために周波数多角形が一般に使用されます。このタイプの図はデータの進化を分析するのに非常に役立つためです。
頻度多角形は、棒グラフまたはヒストグラムの棒の端を結合することによって作成できます。以下では、これがどのように行われるかを見ていきます。
周波数ポリゴンの作成方法
周波数ポリゴンを作成する手順は次のとおりです。
- 周波数多角形の横軸と縦軸を描画し、スケールを作成して、グラフ上にデータを表現できるようにします。
- データのペアをグラフ上の点として表します。
- グラフ上の連続する点を線で結びます。
周波数ポリゴンの例
周波数ポリゴンを構築する方法を正確に理解できるように、以下に例を説明します。
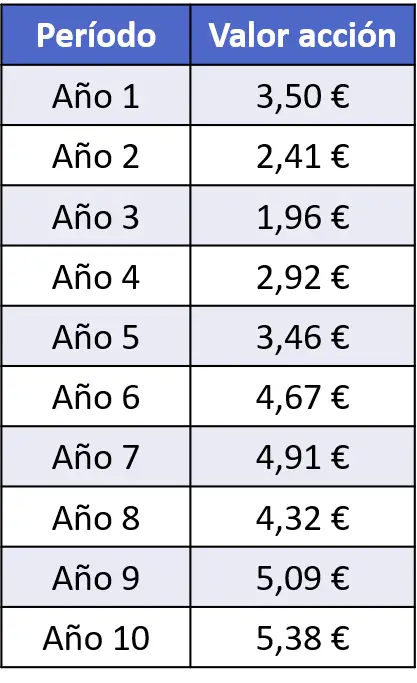
- 次のデータ表は、上場企業の過去 10 年間の株価をまとめたものです。周波数ポリゴンを使用してデータをグラフ化します。
まず第一に、周波数多角形の軸を表す必要があります。横軸に期間を、縦軸に株価を置きます。
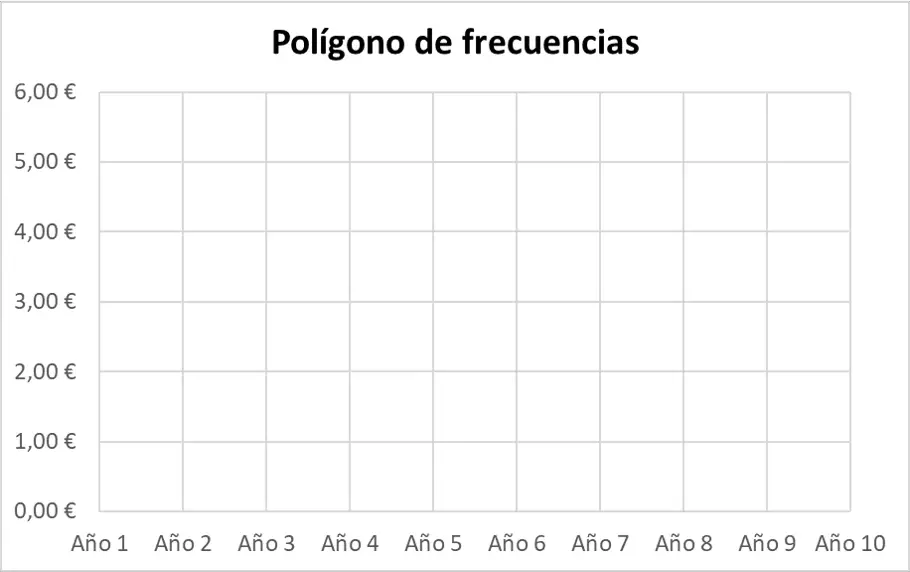
次に、統計データセットを点で表します。各点は、軸上の対応する値からの 2 本の仮想線が交差するグラフ上で表されることに注意してください。
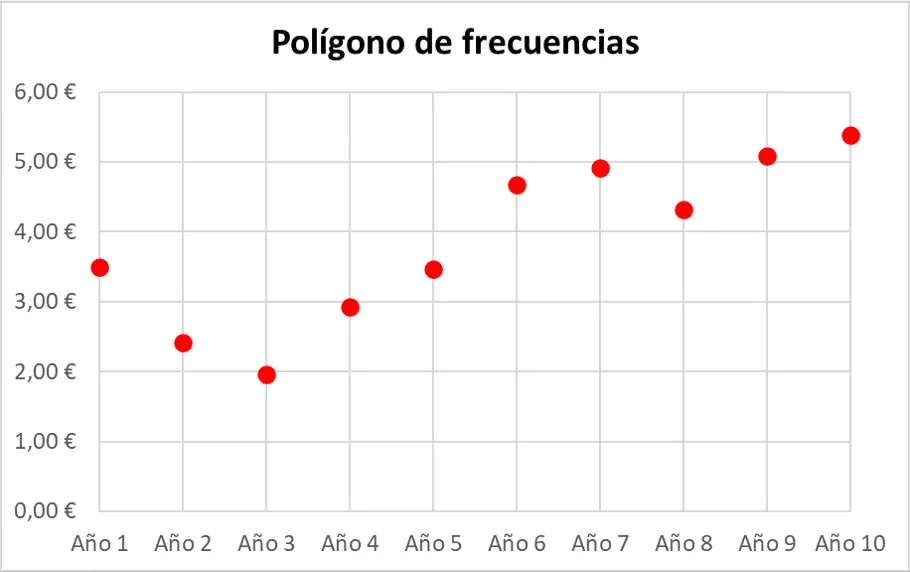
最後に、連続する点を直線で結び、周波数多角形全体の連続線を形成します。
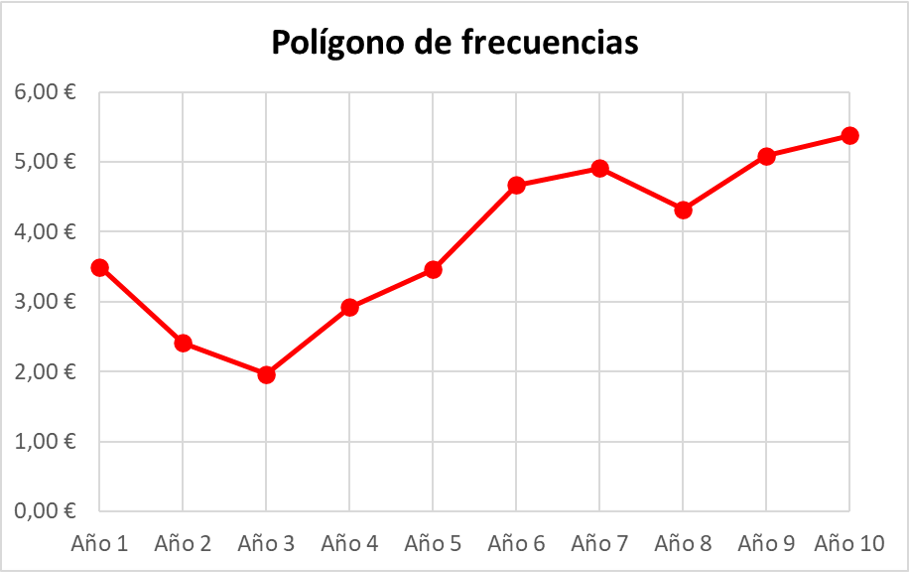
この場合、絶対周波数は周波数多角形で表現されましたが、相対 (またはパーセンテージ) 周波数も表現することもできます。
グループ化されたデータの周波数ポリゴン
変数が離散的な場合に周波数多角形がどのように作成されるかを見てきましたが、周波数多角形は連続変数、つまりデータが間隔にグループ化されている場合にも作成できます。以下に、解決されたそのような例の 1 つを示します。
- 50 人のサンプルサイズが測定され、データは次の度数表に記録されました。周波数ポリゴンを使用してデータをグラフ化します。
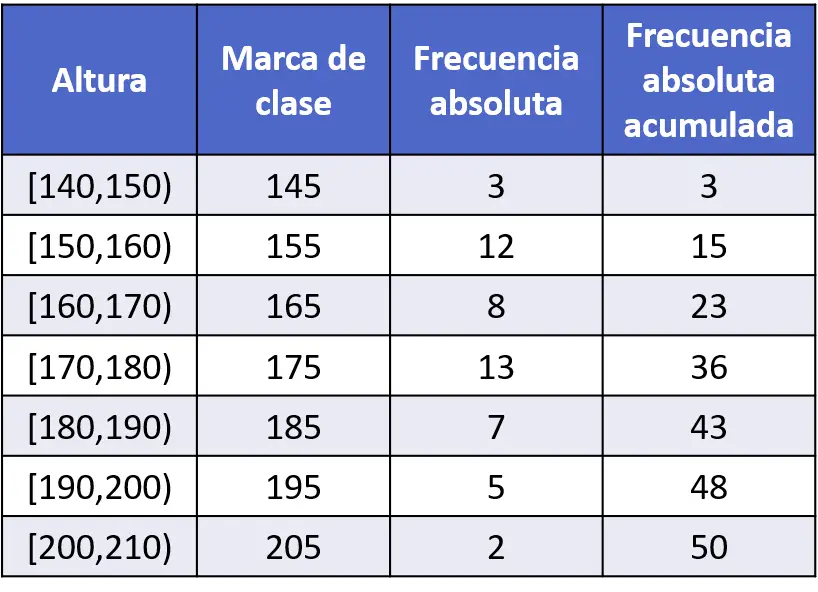
データは間隔ごとにグループ化されているため、周波数多角形の点は各間隔のクラス マーク、つまり間隔の端点の中点にプロットする必要があります。
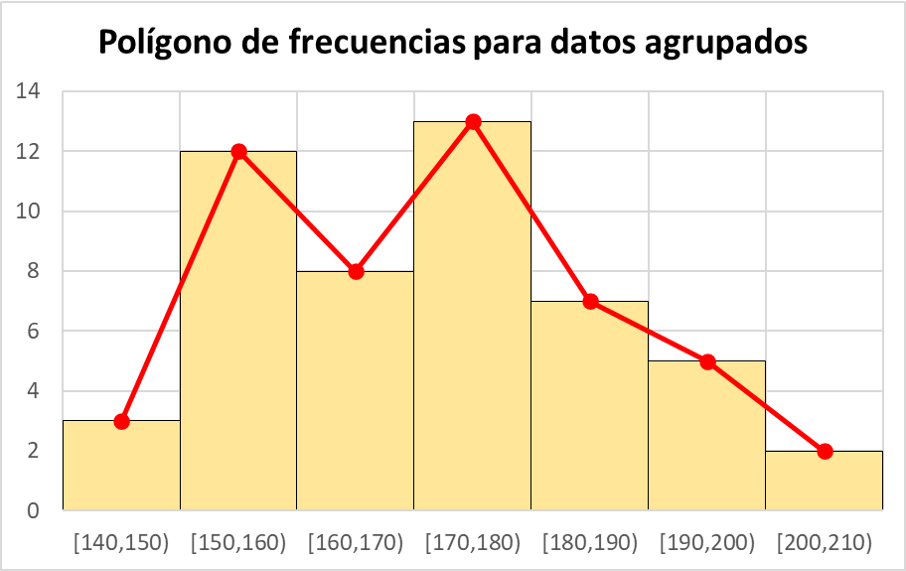
図に示すように、データをグループ化すると、頻度ポリゴンをヒストグラムと組み合わせることができます。実際、最初にヒストグラムを作成する場合、頻度多角形を描画するには、ヒストグラム内の各長方形バーの中点を結合するだけで済みます。
累積周波数ポリゴン
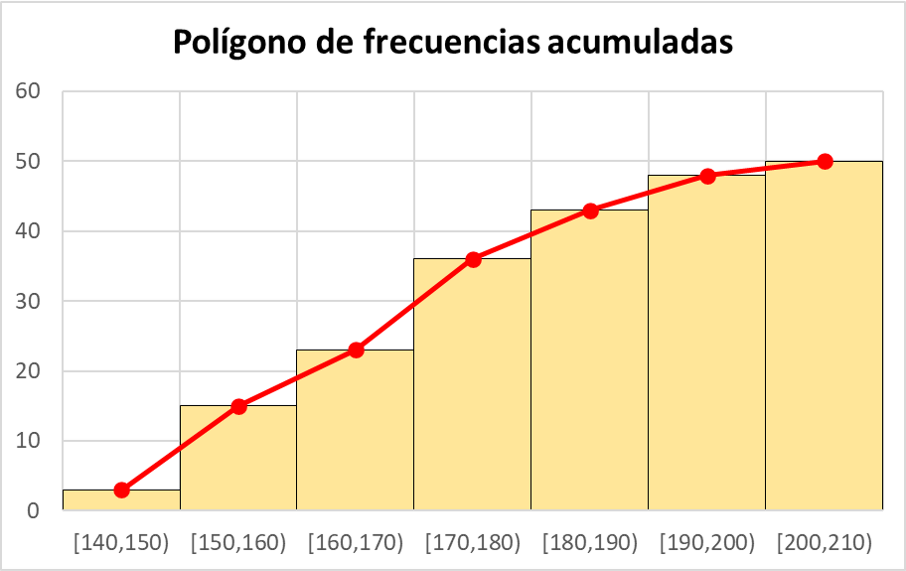
統計では、頻度多角形は累積頻度を表すためにも使用されます。最初にデータ セットの累積度数を計算し、次に絶対度数の代わりに累積度数を使用して周波数多角形内の点を表します。
累積絶対頻度は、以前のすべての絶対頻度と間隔自体の絶対頻度を加算することによって計算されることに注意してください。
例として、以下の前の演習のデータセットからの累積絶対周波数ポリゴンを確認できます。