回帰分析でダミー変数を使用する方法
線形回帰は、1 つ以上の予測変数と応答変数の間の関係を定量化するために使用できる方法です。
通常、 量的変数を使用した線形回帰を使用します。 「数値」変数とも呼ばれるこれらは、測定可能な量を表す変数です。例としては次のものが挙げられます。
- 家の平方フィート数
- 都市の人口規模
- 個人の年齢
ただし、場合によっては、カテゴリ変数を予測変数として使用したいことがあります。これらは名前またはラベルを取り、カテゴリに分類できる変数です。例としては次のものが挙げられます。
- 目の色(例:「青」、「緑」、「茶色」)
- 性別(例:「男性」、「女性」)
- 婚姻状況(例:「既婚」、「独身」、「離婚」)
カテゴリカル変数を使用する場合、「青」、「緑」、「茶色」などの値に 1、2、3 のような値を割り当てるだけでは意味がありません。その緑は二重です。青や茶色と同じくらいカラフルな色は、青の 3 倍カラフルです。
代わりに、ダミー変数を使用することが解決策です。これらは回帰分析専用に作成される変数で、0 または 1 の 2 つの値のいずれかをとります。
ダミー変数: 2 つの値 (0 または 1) のいずれか 1 つだけを取ることができるカテゴリ データを表すために回帰分析で使用される数値変数。
作成する必要があるダミー変数の数はk -1 に等しくなります。ここで、 kはカテゴリ変数が取ることができるさまざまな値の数です。
次の例は、さまざまなデータセットのダミー変数を作成する方法を示しています。
例 1: 値が 2 つだけあるダミー変数を作成する
次のデータセットがあり、性別と年齢を使用して収入を予測したいとします。
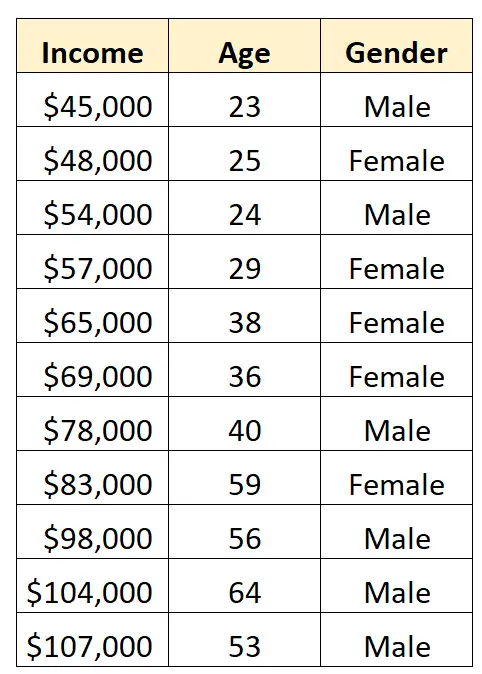
性別を回帰モデルの予測変数として使用するには、性別をダミー変数に変換する必要があります。
これは現時点では 2 つの異なる値 (「男性」または「女性」) を取ることができるカテゴリ変数であるため、単純にk -1 = 2-1 = 1 のダミー変数を作成します。
このダミー変数を作成するには、0 を表す値 (「男性」または「女性」) の 1 つを選択し、1 を表すもう 1 つの値を選択します。
一般に、最も頻繁に使用される値は 0 で表され、このデータセットでは「男性」になります。
したがって、性別をダミー変数に変換する方法は次のとおりです。
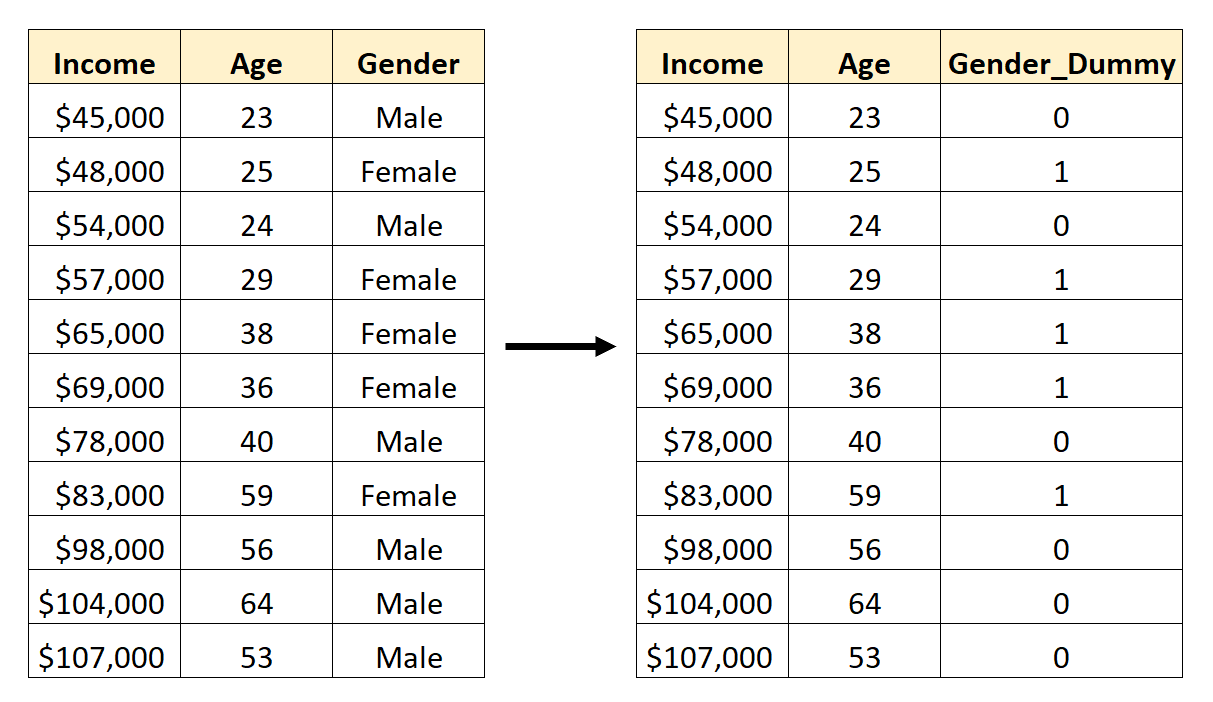
その後、 AgeとGender_Dummy を回帰モデルの予測変数として使用できます。
例 2: 複数の値を持つダミー変数を作成する
次のデータセットがあり、婚姻状況と年齢を使用して収入を予測したいとします。

婚姻状況を回帰モデルの予測変数として使用するには、それをダミー変数に変換する必要があります。
これは現在、3 つの異なる値 (「独身」、「既婚」、または「離婚」) を取ることができるカテゴリ変数であるため、 k -1 = 3-1 = 2 個のダミー変数を作成する必要があります。
このダミー変数を作成するには、最も頻繁に表示される「Single」を基本値としてそのままにしておきます。したがって、婚姻状況をダミー変数に変換する方法は次のとおりです。

その後、回帰モデルの予測変数としてAge 、 Married 、 Divorcedを使用できます。
ダミー変数を使用した回帰出力を解釈する方法
前の例のデータセットを使用し、予測変数としてAge 、 Married 、およびDivorced 、応答変数としてIncomeを使用して重線形回帰モデルを近似するとします。
回帰の結果は次のとおりです。
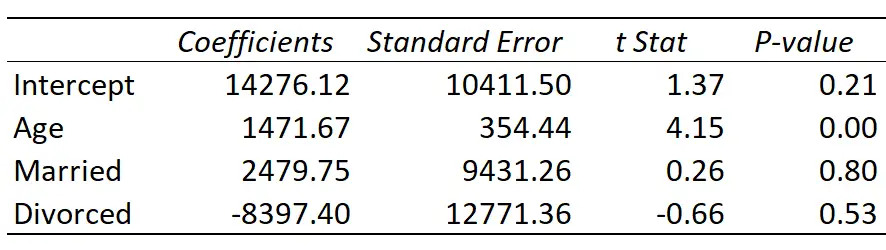
近似回帰直線は次のように定義されます。
収入 = 14,276.21 + 1,471.67*(年齢) + 2,479.75*(既婚) – 8,397.40*(離婚)
この方程式を使用して、年齢と婚姻状況に基づいて個人の推定収入を求めることができます。たとえば、35 歳で既婚者の推定収入は68,264 ドルになります。
収入 = 14,276.21 + 1,471.67*(35) + 2,479.75*(1) – 8,397.40*(0) = 68,264 ドル
表内の回帰係数を解釈する方法は次のとおりです。
- 切片:切片は、0 歳の独身者の平均収入を表します。明らかに、ゼロ年を持つことはできないため、この特定の回帰モデルで切片を単独で解釈することは意味がありません。
- 年齢:年齢が上がるごとに、収入は平均 1,471.67 ドル増加します。 p 値 (0.00) は 0.05 未満であるため、年齢は統計的に有意な収入の予測因子となります。
- 既婚者:既婚者の収入は、独身者よりも平均で 2,479.75 ドル高くなります。 p 値 (0.80) は 0.05 未満ではないため、この差は統計的に有意ではありません。
- 離婚者:離婚者の収入は、独身者より平均 8,397.40 ドル少ないです。 p 値 (0.53) は 0.05 未満ではないため、この差は統計的に有意ではありません。
どちらのダミー変数も統計的に有意ではなかったため、収入に予測値を追加するようには見えないため、婚姻状況を予測変数としてモデルから削除することができました。