回帰勾配の有意性をテストする方法

12 軒の異なる住宅の面積と価格を示す次のデータセットがあるとします。

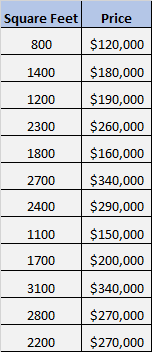
面積と価格の間に有意な関係があるかどうかを知りたいと考えています。

データがどのようなものかを把握するために、まず、X 軸に平方フィート、Y 軸に価格を設定した散布図を作成します。

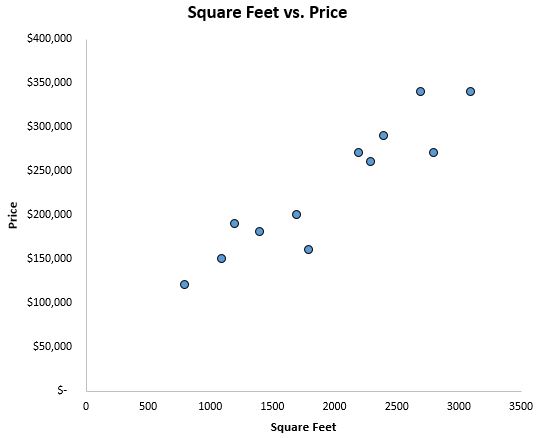
面積と価格の間に正の相関関係があることがはっきりとわかります。面積が増えると住宅価格も上がる傾向にあります。

ただし、面積と価格の間に統計的に有意な関係があるかどうかを確認するには、単純な線形回帰を実行する必要があります。

そこで、予測変数として平方フィート、応答として価格を使用して単純な線形回帰を実行すると、次の結果が得られます。

Excel、SPSS、R、またはその他のソフトウェアで単純な線形回帰を実行すると、上に示したものと同様の結果が得られます。

単純な線形回帰により、散布図のデータに最もよく「適合」する直線の方程式である最良適合直線が生成されることに注意してください。この最適な線は次のように定義されます。

ŷ = b ₀ + b ₁ x

ここで、ŷ は応答変数の予測値、b ₀は切片、b ₁は回帰係数、x は予測変数の値です。

b ₀の値は、原点の係数、 47588.70 によって与えられます。

b ₁の値は、予測子変数Square Feetの係数、 93.57 によって与えられます。

したがって、この例の最適な直線はŷ = 47588.70+ 93.57xとなります。

この最適な線を解釈する方法は次のとおりです。

• b ₀ :平方フィートの値がゼロの場合、期待される平均価格値は $47,588.70 です。 (この場合、家の面積がゼロ平方フィートになることはありえないため、切片を解釈することはあまり意味がありません)
• b ₁ :平方フィートが追加されるごとに、価格の平均予想上昇額は 93.57 ドルになります。

したがって、平方フィートが追加されるごとに、予想される価格の平均上昇額は 93.57 ドルであることがわかりました。

この増加が統計的に有意であるかどうかを知るには、B ₁の仮説検定を実行するか、B ₁の信頼区間を構築する必要があります。

注: 仮説検定と信頼区間では、常に同じ結果が得られます。

回帰勾配の信頼区間の構築

回帰勾配の信頼区間を構築するには、次の式を使用します。

信頼区間 = b ₁ +/- (t _{1-∝/2, n-2} ) * (b ₁の標準誤差)

金：

• b ₁は回帰結果で与えられる傾き係数です。
• (t _{1-∝/2, n-2} ) は、n-2 自由度の 1-∝ 信頼水準の臨界 t 値です。ここで、 nはデータセット内の観測値の総数です。
• (b ₁の標準誤差) は、回帰結果で与えられる b ₁の標準誤差です。

この例では、B ₁の 95% 信頼区間を構築する方法を次に示します。

• b _{1 は}回帰出力から 93.57 です。
• 95% 信頼区間、∝ = 0.05、n-2 = 12-2 = 10 を使用しているため、t 分布表によれば_{、t 0.975、10}は 2.228 となります。
• ( _b1の標準誤差) は、回帰出力から 11.45 です。

したがって、B ₁の 95% 信頼区間は次のようになります。

93.57 +/- (2.228) * (11.45) = (68.06, 119.08)

これは、追加平方フィートごとの真の平均価格上昇が 68.06 ドルから 119.08 ドルの間であると 95% 確信していることを意味します。

$0 はこの範囲内にないため、平方フィートと価格の関係は 95% の信頼水準で統計的に有意であることに注意してください。

回帰勾配の仮説検定を実行する

回帰勾配の仮説検定を実行するには、仮説検定の 5 つの標準的な手順に従います。

ステップ 1. 仮説を述べます。

帰無仮説 (H0): B ₁ = 0

対立仮説: (Ha): B ₁ ≠ 0

ステップ 2. 使用する有意水準を決定します。

前の例で 95% 信頼区間を構築したため、ここでは同等のアプローチを使用し、有意水準 0.05 を使用することを選択します。

ステップ 3. 検定統計量と対応する p 値を見つけます。

この場合、検定統計量は、自由度 n-2 のt = b ₁の係数 / b ₁の標準誤差です。回帰結果からこれらの値を見つけることができます。

したがって、検定統計量t = 92.89 / 13.88 = 6.69 となります。

10 自由度および両側検定でスコア 6.69のT スコア対 P 値計算ツールを使用すると、p 値 = 0.000 となります。

ステップ 4. 帰無仮説を拒否するか、拒否しません。

p 値が有意水準 0.05 を下回っているため、帰無仮説を棄却します。

ステップ 5. 結果を解釈します。

帰無仮説を棄却したため、追加平方フィートごとの真の平均価格上昇はゼロではないと言える十分な証拠が得られました。