基準の妥当性の簡単な説明
基準の妥当性とは、ある変数の測定値が別の変数の応答を予測する能力を指します。
一方の変数は説明変数と呼ばれ、もう一方の変数は基準変数と呼ばれます。
たとえば、特定の大学の入学試験が生徒の第 1 学期の成績平均点をどの程度予測できるかを知りたい場合があります。
入学試験が説明変数、基準変数が前期GPAとなります。
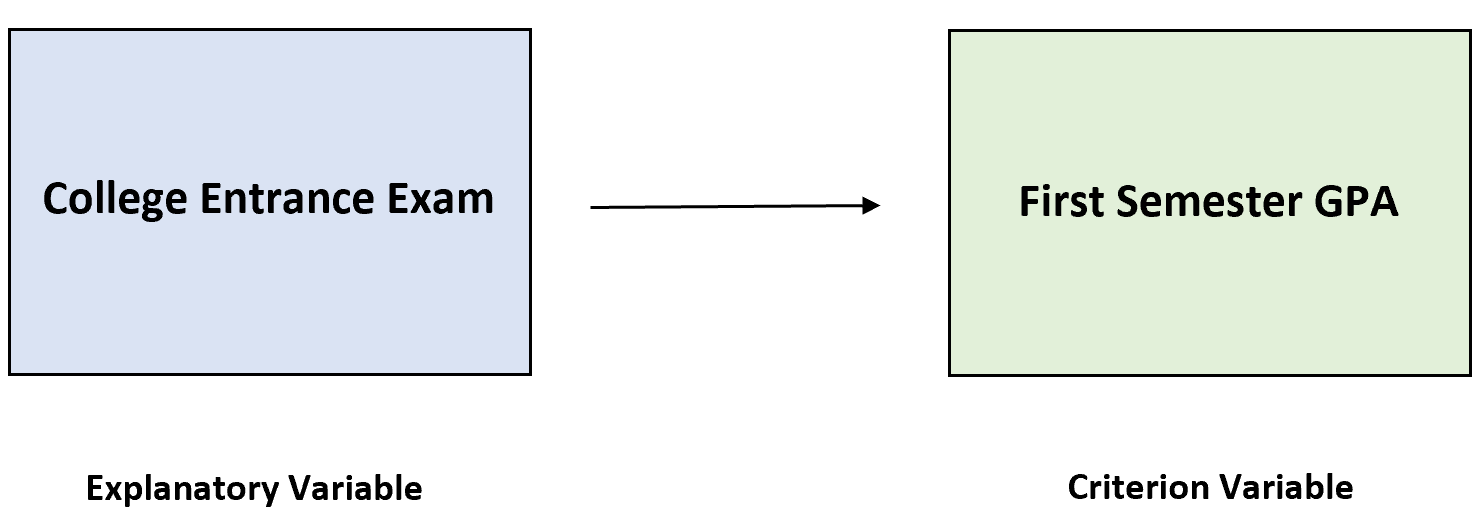
基準変数を予測する手段としてこの特定の説明変数を使用することが有効かどうかを知りたいと考えています。
基準の妥当性を測定する方法
通常、基準の妥当性は ピアソン相関係数などの指標を使用して測定します。ピアソン相関係数は -1 から 1 までの値を取ります。
- -1 は、2 つの変数間の完全な負の線形相関を示します。
- 0 は 2 つの変数間に線形相関がないことを示します
- 1 は、2 つの変数間の完全な正の線形相関を示します。
相関係数がゼロから離れるほど、2 つの変数間の関連性が強くなります。
たとえば、1,000 人の学生の入学試験の得点と前期 GPA のデータを収集し、2 つの変数間の相関関係が0.843であることが判明した場合、これは 2 つの変数の相関性が高いことを意味します。
つまり、入学試験の得点が高い生徒は、1学期の得点も高い傾向にあります。逆に、入学試験の得点が低い学生は、最初の学期の GPA が低い傾向があります。
基準の有効性の種類
基準の妥当性には主に 2 つのタイプがあります。
1.予測の妥当性
基準の妥当性の 1 つ目のタイプは予測妥当性として知られており、変数の測定値が将来の変数の測定値を正確に予測できるかどうかを判断します。
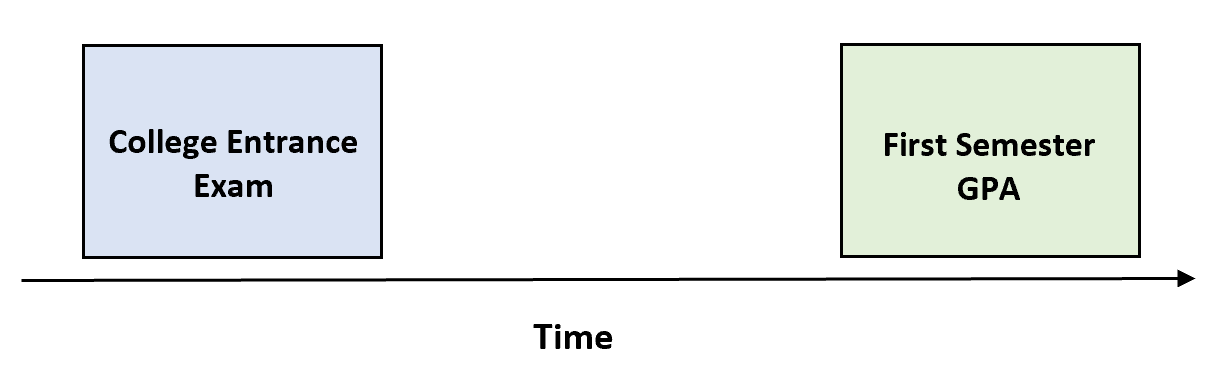
学生の大学入学試験のスコアと最初の学期の GPA を測定する前述の例は、2 つの変数を異なる時点で測定しているため、予測の妥当性を測定する例です。
つまり、入学試験の成績から前期の GPA をうまく予測できるかどうかを判断しようとします。
2.同時有効性
2 番目のタイプの基準妥当性は同時妥当性として知られており、2 つの変数を同時に(つまり同時に) 測定して、一方の変数が他方の変数と有意に関連しているかどうかを確認します。
この例としては、企業が特定の種類のテストを実施して、テスト結果が従業員の生産性と相関しているかどうかを確認する場合が挙げられます。
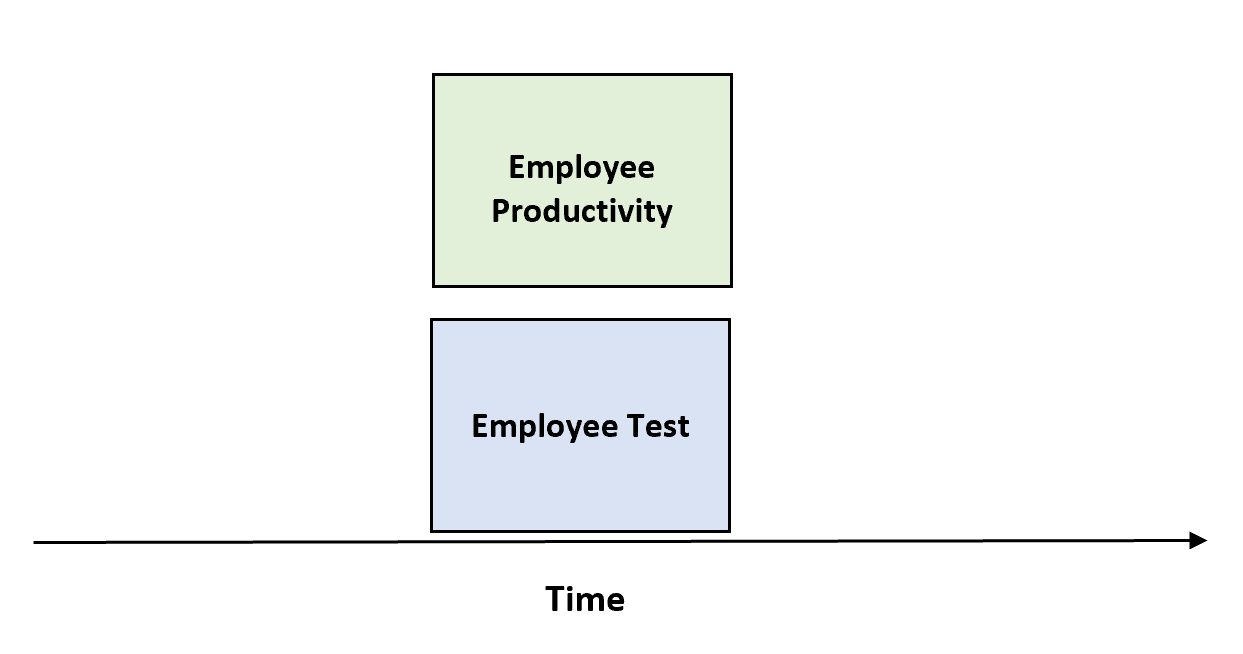
このアプローチの利点は、対象となる変数基準の測定を行うために、将来しばらく待つ必要がないことです。