外れ値を含む箱ひげ図を読み取る方法 (例付き)

箱ひげ図は、データ セットの 5 桁の概要を表示するプロットの一種で、次のものが含まれます。

• 最小値
• 最初の四分位数 (25 パーセンタイル)
• 中央値
• 第 3 四分位数 (75 パーセンタイル)
• 最大値

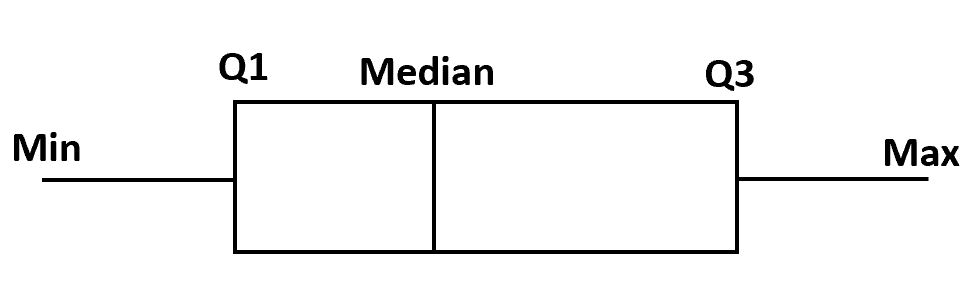
箱ひげ図を作成するには、まず第 1 四分位から第 3 四分位までの箱を描画します。

次に、中央値に垂直線を引きます。

最後に、最小値と最大値までの四分位の「ひげ」を描画します。

ほとんどの統計ソフトウェアでは、次の 2 つの要件のいずれかを満たしている場合、観測値は外れ値として定義されます。

• 観測値は、第 1 四分位 (Q1) より下の四分位範囲の 1.5 倍です。
• 観測値は、第 3 四分位 (Q3) より上の四分位範囲の 1.5 倍です。

データセットに外れ値が存在する場合、通常、箱ひげ図のひげの範囲の外側に小さな点でラベルが付けられます。

この場合、箱ひげ図の「最小」値と「最大」値には、それぞれ Q1 – 1.5*IQR と Q3 + 1.5*IQR の値が割り当てられるだけです。

次の例は、外れ値がある場合とない場合の箱ひげ図を解釈する方法を示しています。

例: 外れ値を含む箱ひげ図の解釈

次の 2 つの箱ひげ図を作成して、2 つの異なるチームのバスケットボール選手が獲得したポイントの分布を視覚化するとします。

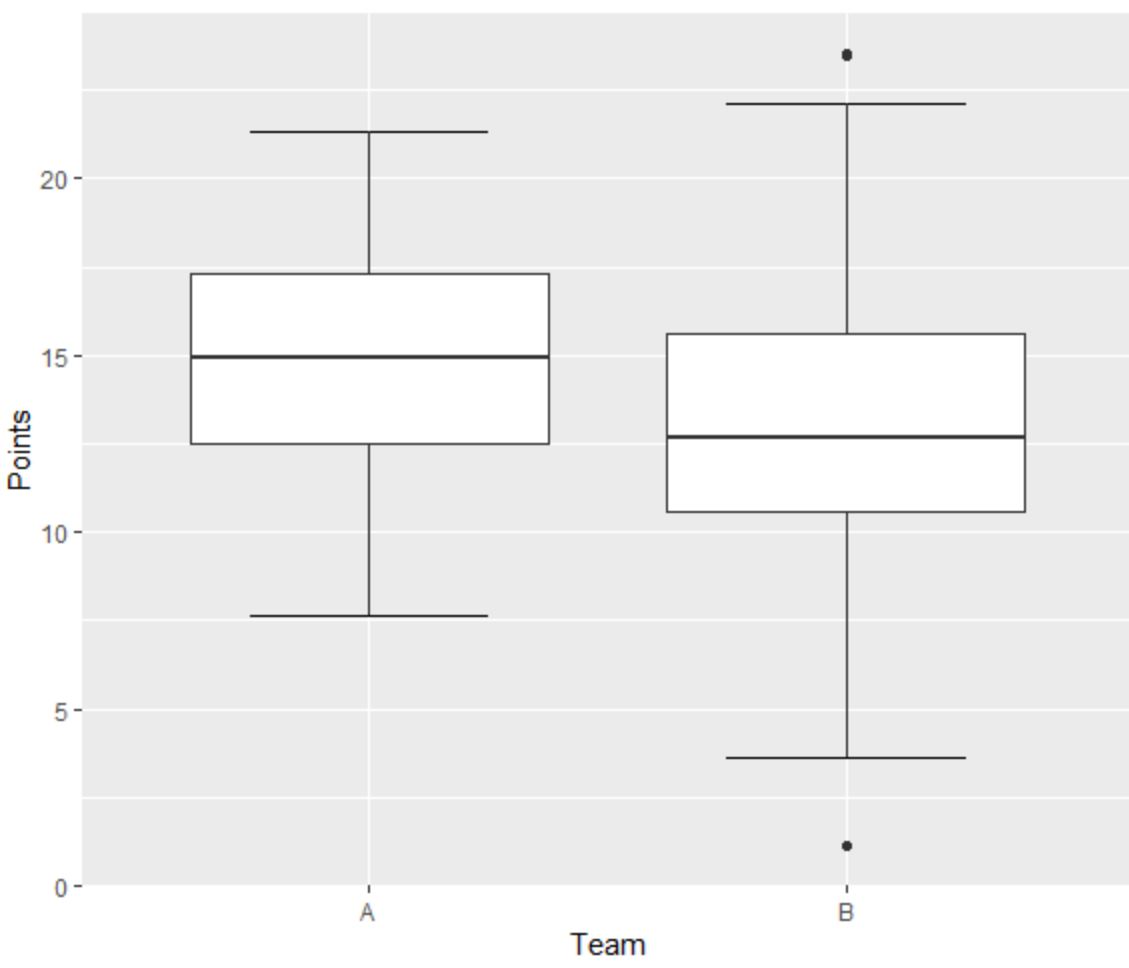
チーム A の左側の箱ひげ図には、最小または最大のひげの外側に小さな点がないため、外れ値はありません。

ただし、チーム B の右側の箱ひげ図には、「最大」値を上回る外れ値が 1 つと、「最小」値を下回る外れ値が 1 つあります。

以下は、チーム B の「ポイント」変数の分布に関する現在の 5 桁の要約です。

• 最小値: 1.1
• 最初の四分位: 10.5
• 中央値: 12.7
• 第 3 四分位: 15.6
• 最大値：23.5

潜在的な外れ値の制限を計算する方法は次のとおりです。

四分位スケール: 第 3 四分位 – 第 1 四分位 = 15.6 – 10.5 = 5.1

下限値: Q1 – 1.5*IQR = 10.5 – 1.5*5.1 = 2.85

上限値：Q3 + 1.5*IQR = 15.6 + 1.5*5.1 = 23.25

箱ひげ図の最小値と最大値のひげは2.85と23.25に配置されます。

したがって、値1.1と23.5の観測値は両方とも下限と上限の範囲外にあるため、箱ひげ図では外れ値として認定されます。

おまけ: R プログラミング言語でこれら 2 つの箱ひげ図を作成するために使用した正確なコードは次のとおりです。

 library (ggplot2)

#make this example reproducible 
set. seeds (2)

#create data frame
df <- data. frame (Team = factor(rep(c("A", "B"), each = 200)), 
                 Points = c(rnorm(200, mean = 15, sd = 3), 
                           rnorm(200, mean = 12, sd = 4))) 

#create box plots
ggplot(df, aes(x = Team, y = Points)) +
  stat_boxplot(geom = " errorbar ", width = 0.5) +  
  geom_boxplot() 

#calculate summary statistics for each team
tapply(df$Points, df$Team, summary)

追加リソース

次のチュートリアルでは、箱ひげ図に関する追加情報を提供します。

箱ひげ図を比較する方法
箱ひげ図で非対称性を特定する方法
箱ひげ図の四分位範囲を見つける方法