Excel で多項式回帰を実行する方法
回帰分析は、1 つ以上の説明変数と応答変数の間の関係を定量化するために使用されます。
回帰分析の最も一般的なタイプは単純線形回帰で、説明変数と応答変数が線形関係にある場合に使用されます。
ただし、説明変数と応答変数の関係が非線形になる場合があります。
このような場合、変数間の非線形関係を説明できる多項式回帰を使用することが合理的です。
このチュートリアルでは、Excel で多項式回帰を実行する方法について説明します。
例: Excel での多項式回帰
Excel に次のデータ セットがあるとします。
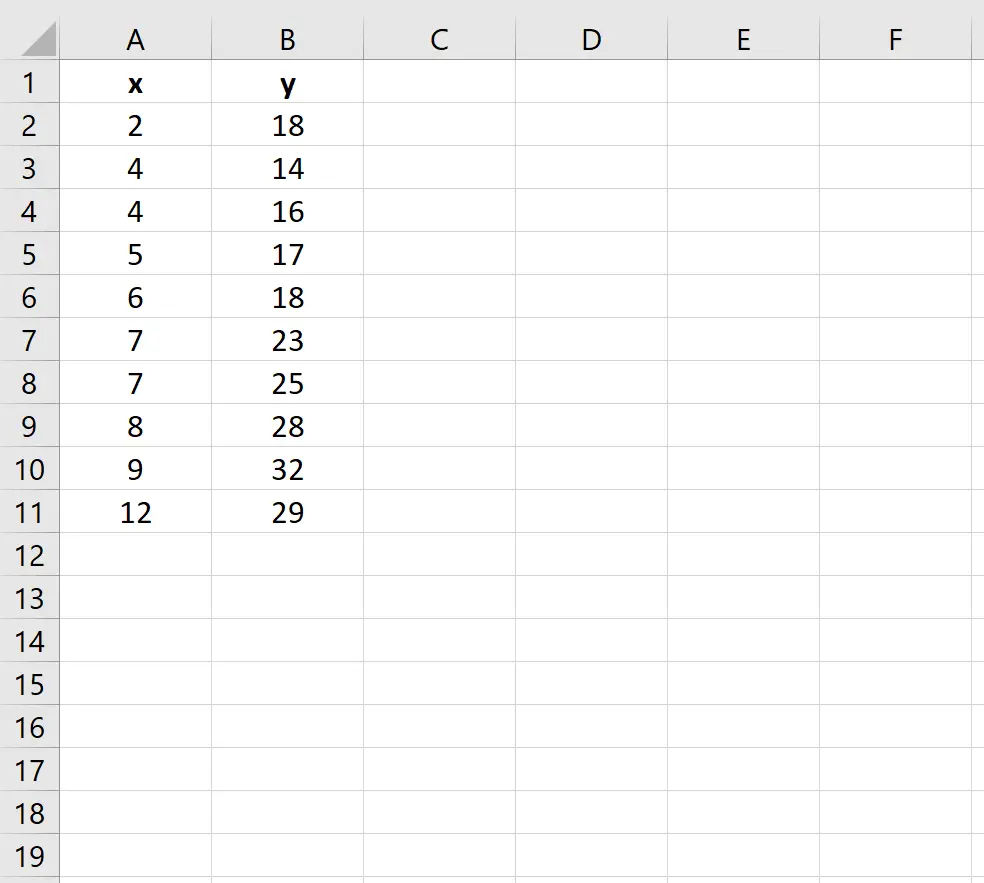
多項式回帰式をこのデータセットに当てはめるには、次の手順を実行します。
ステップ 1: 散布図を作成します。
まず、散布図を作成する必要があります。 [挿入]タブの[グラフ]グループに移動し、 [散布図]の最初のグラフ タイプをクリックします。
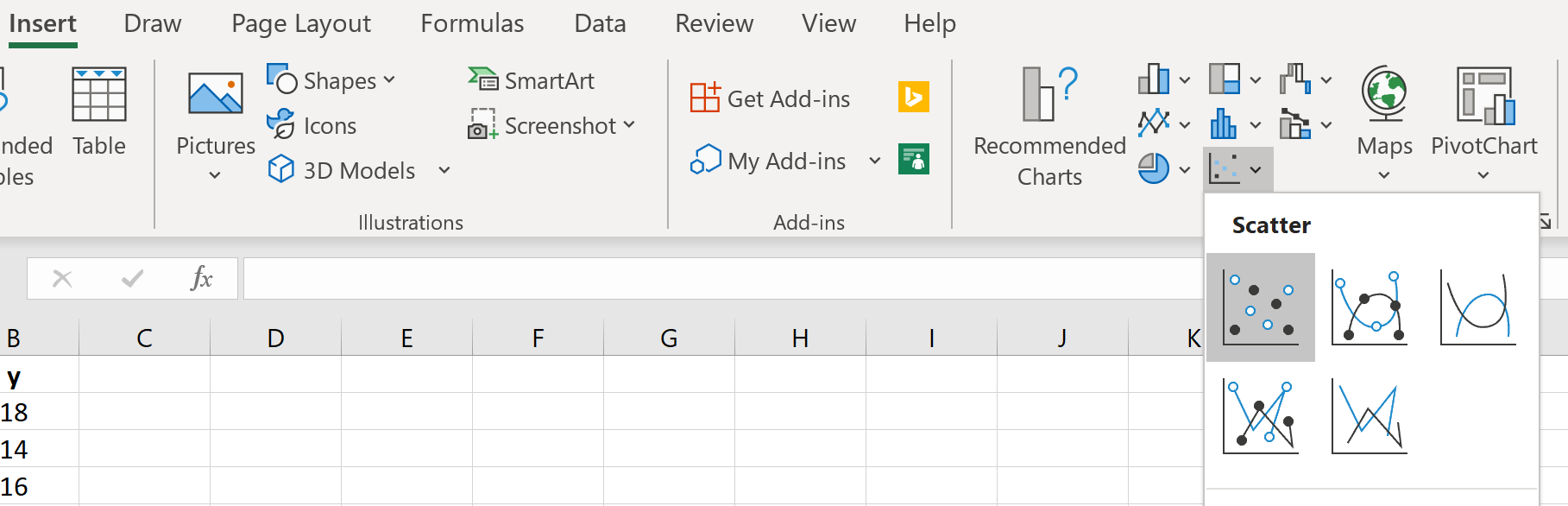
点群が自動的に表示されます。
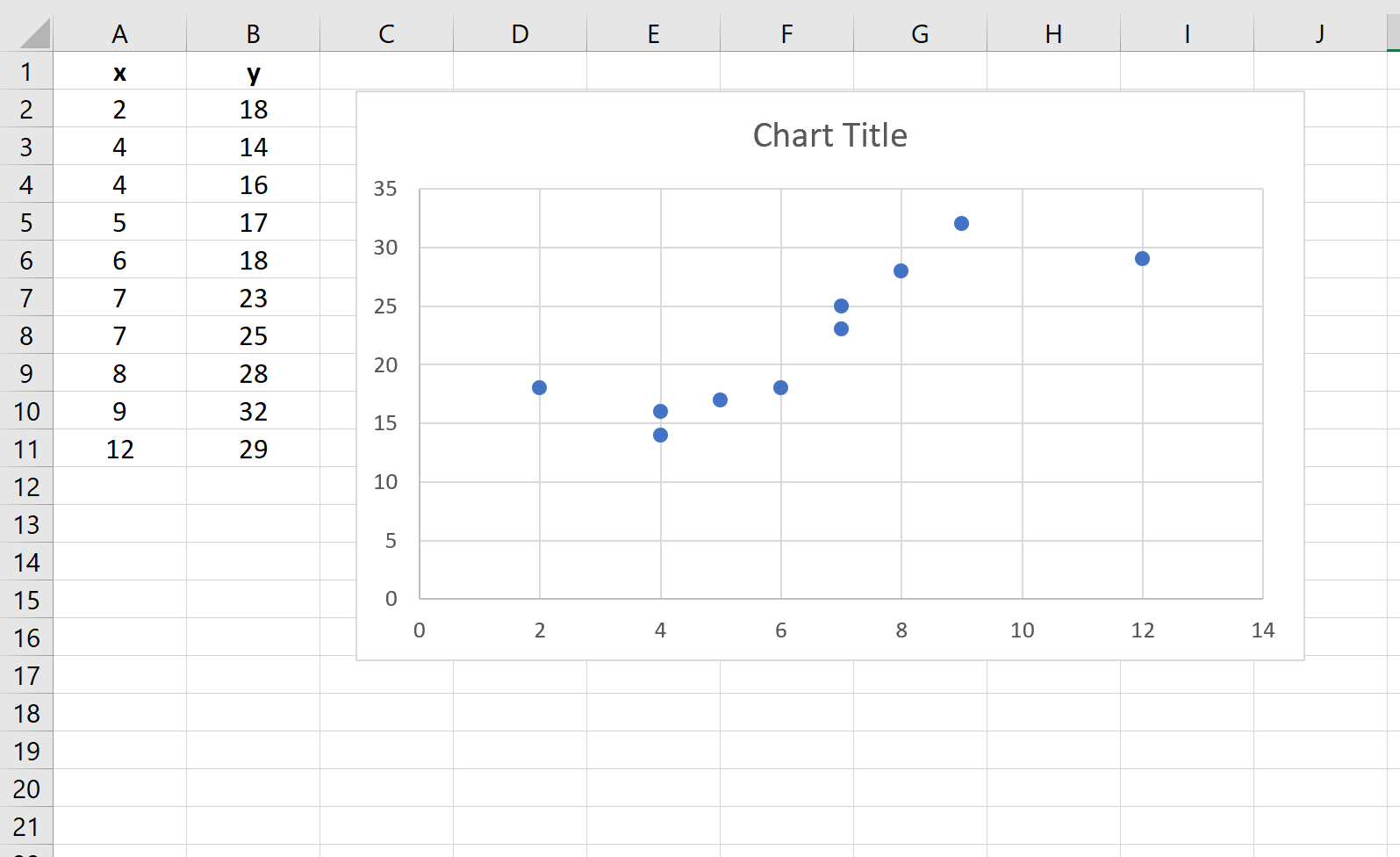
ステップ 2: 傾向線を追加します。
次に、散布図に傾向線を追加する必要があります。これを行うには、点群内の個々の点の 1 つをクリックします。次に、右クリックして「トレンドラインの追加…」を選択します。
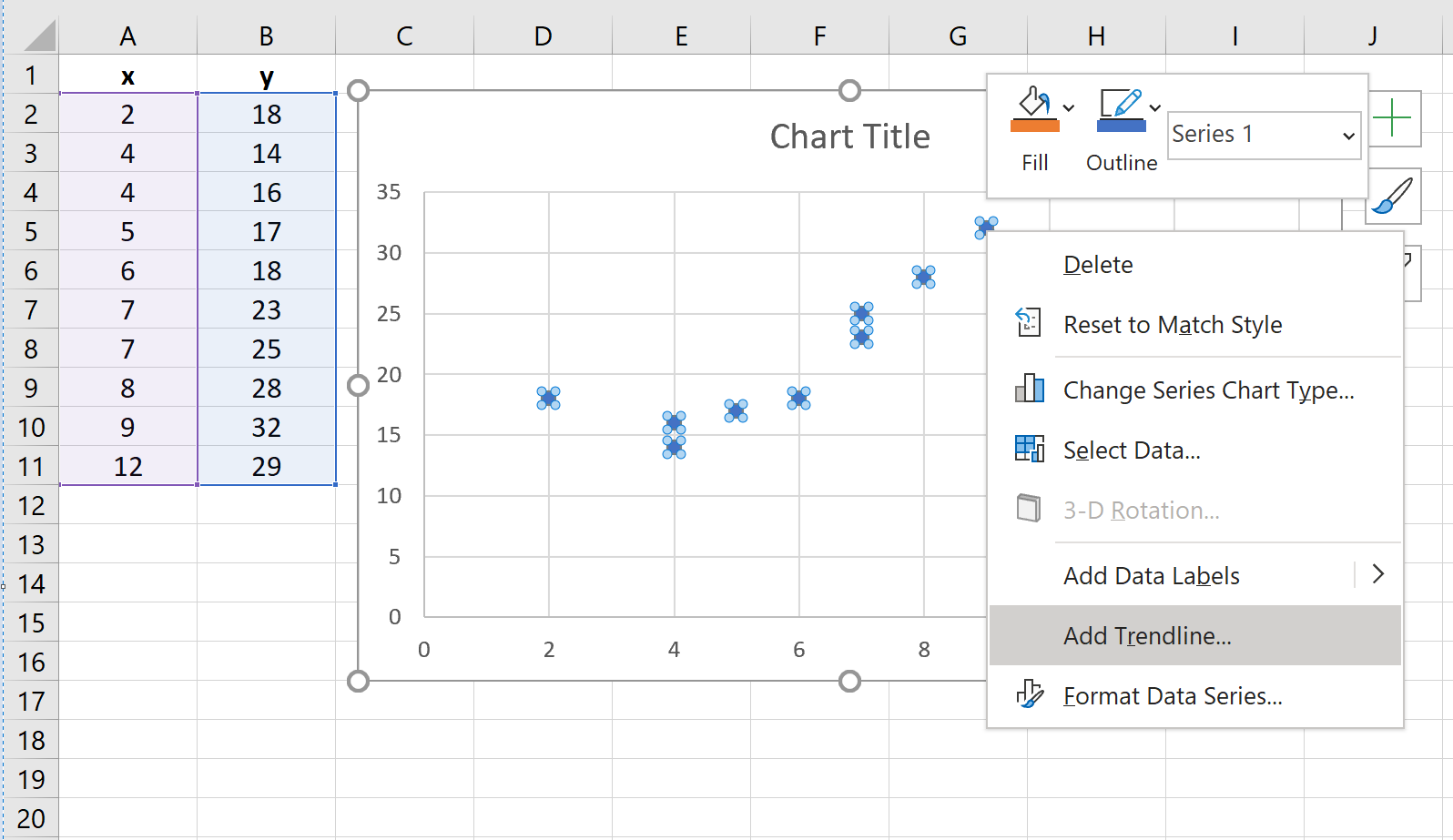
新しいウィンドウが表示され、傾向線を指定するオプションが表示されます。 [多項式]を選択し、 [次数]に使用する数値を選択します。 3 を使用します。次に、下部にある[グラフに数式を表示]チェックボックスをオンにします。
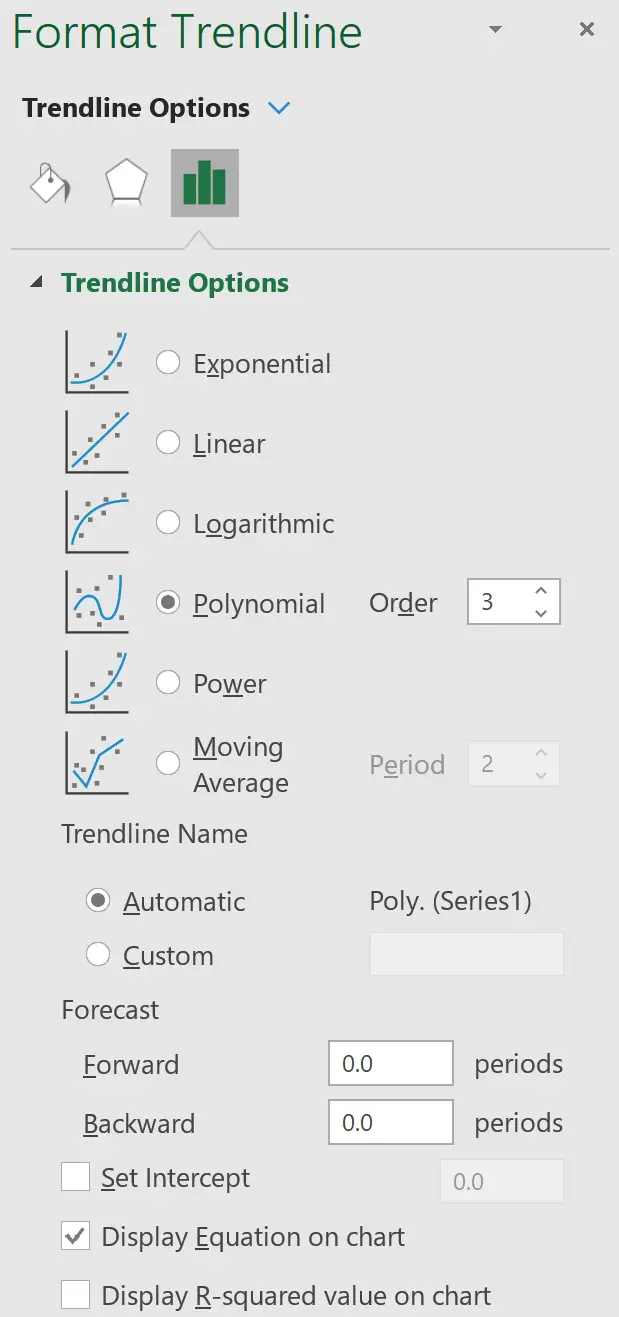
多項式回帰式を含む傾向線が散布図に自動的に表示されます。
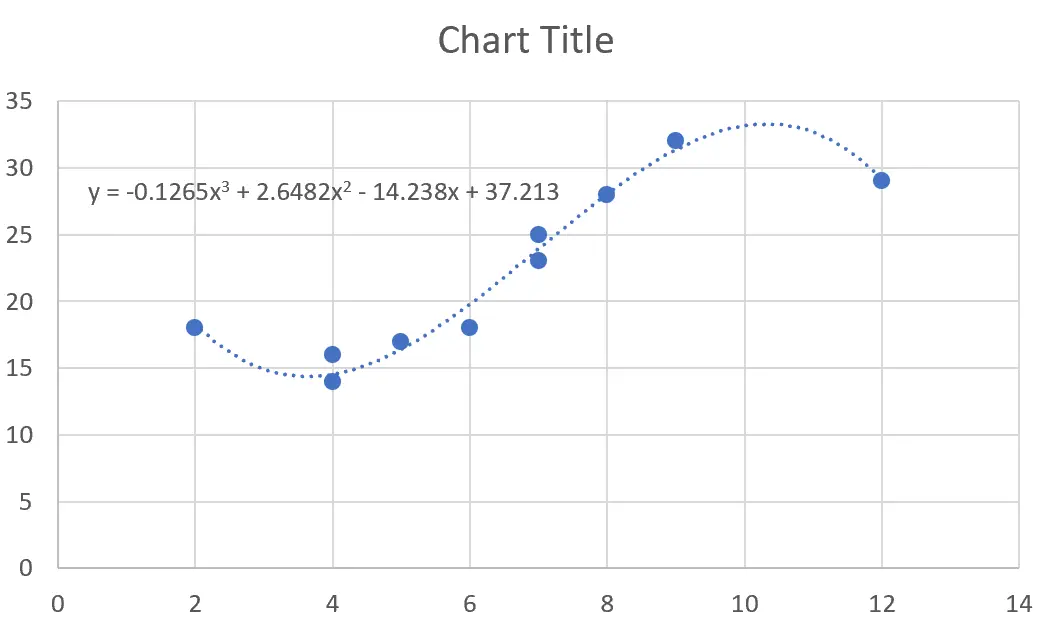
ステップ 3: 回帰式を解釈します。
この特定の例では、近似された多項式回帰式は次のようになります。
y = -0.1265x 3 + 2.6482x 2 – 14.238x + 37.213
この方程式を使用すると、説明変数の特定の値が与えられた場合の応答変数の期待値を見つけることができます。たとえば、x = 4 と仮定します。応答変数 y の期待値は次のようになります。
y = -0.1265(4) 3 + 2.6482(4) 2 – 14.238(4) + 37.213 = 14.5362 。