多項式回帰
この記事では、統計における多項式回帰とは何か、およびそれがどのように実行されるかについて説明します。さらに、多項式回帰が実行される例も確認できます。
多項式回帰とは何ですか?
多項式回帰、または多項式回帰 は、独立変数 X と従属変数 Y の間の関係が多項式を使用してモデル化される回帰モデルです。
たとえば、2 次多項式回帰モデルの方程式は、y=β 0 +β 1 x+β 2 x 2 +ε です。
多項式回帰は、グラフが多項式曲線であるデータ セットを近似するのに役立ちます。したがって、データ サンプルのドット プロットが放物線の形状をしている場合は、線形回帰モデルよりも二次回帰モデルを構築する方が適切です。こうすることで、回帰モデルの方程式がデータ サンプルによりよく適合します。
多項式回帰は、指数回帰や対数回帰と同様、非線形回帰の一種であることに注意してください。
多項式回帰式
多項式回帰モデルの方程式は、y=β 0 +β 1 x+β 2 x 2 +β 3 x 3 …+β m x m +ε です。
![]()
金:
-

は従属変数です。
-

は独立変数です。
-

は多項式回帰式の定数です。
-

変数に関連付けられた回帰係数です

。
-

これは誤差または残差、つまり観測値とモデルによって推定された値の差です。
したがって、合計が含まれるサンプルがある場合、
![]()
観察結果を基に、行列形式の多項式回帰モデルを提案できます。
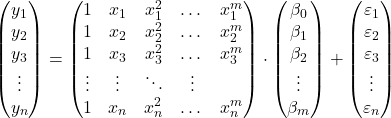
上記の行列式は、各行列に文字を割り当てることで書き換えることができます。
![]()
したがって、最小二乗基準を適用すると、多項式回帰モデルの係数を推定するための式に到達できます。
![]()
ただし、これらの計算を手作業で行うのは非常に面倒で時間がかかるため、多項式回帰モデルをより高速に実行できるコンピューター ソフトウェア (Minitab や Excel など) を使用する方が便利です。
多項式回帰モデルの例
多項式回帰の定義とその実行方法がわかったので、概念を完全に理解するために実際の例を見てみましょう。
まず、データ グラフが多項式曲線の形状をしている場合、多項式回帰モデルを実行する必要があることに留意する必要があります。たとえば、ドットプロットが 3 次曲線の形式である場合、3 次多項式回帰モデルを構築する必要があります。
したがって、次の画像に見られるように、独立変数の値が増加すると従属変数の増加が速くなるため、データのドット プロットは二次形状になります。この場合、線形回帰モデルが実行されましたが、見てわかるように、線がすべての点の下にあるセクションと線がすべての点の上にあるセクションがあるため、点がうまく適合しません。
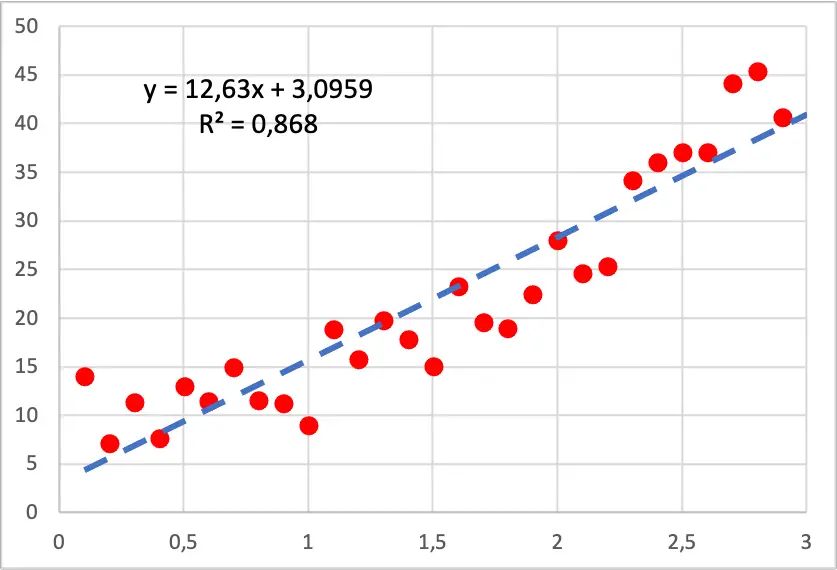
一方、2次多項式回帰モデルを実行すると、以下の画像でわかるように、サンプル データによりよく適合します。

さらに、多項式回帰モデルを作成すると、決定係数が 86.80% から 94.05% に向上し、大幅に向上します。したがって、新しい回帰モデルはデータセットをより適切に説明します。
一方、多項式回帰を実行する必要があることを示すもう 1 つの兆候は、残差のプロットです。線形回帰で残差のグラフが放物線または別のタイプの多項式の形状をしている場合、多項式回帰モデルは調査されたデータにより確実に適合します。
他のタイプの非線形回帰
非線形回帰には主に 3 つのタイプがあります。
- 多項式回帰– 回帰モデルの方程式は多項式の形式です。
- 対数回帰: 独立変数の対数が取得されます。
- 指数回帰: 独立変数は方程式の指数で見つかります。