Google スプレッドシートでの多項式回帰 (ステップバイステップ)
回帰分析は、1 つ以上の予測変数と応答変数の間の関係を定量化するために使用されます。
最も一般的なタイプの回帰分析は単純線形回帰で、予測変数と応答変数が線形関係にある場合に使用されます。
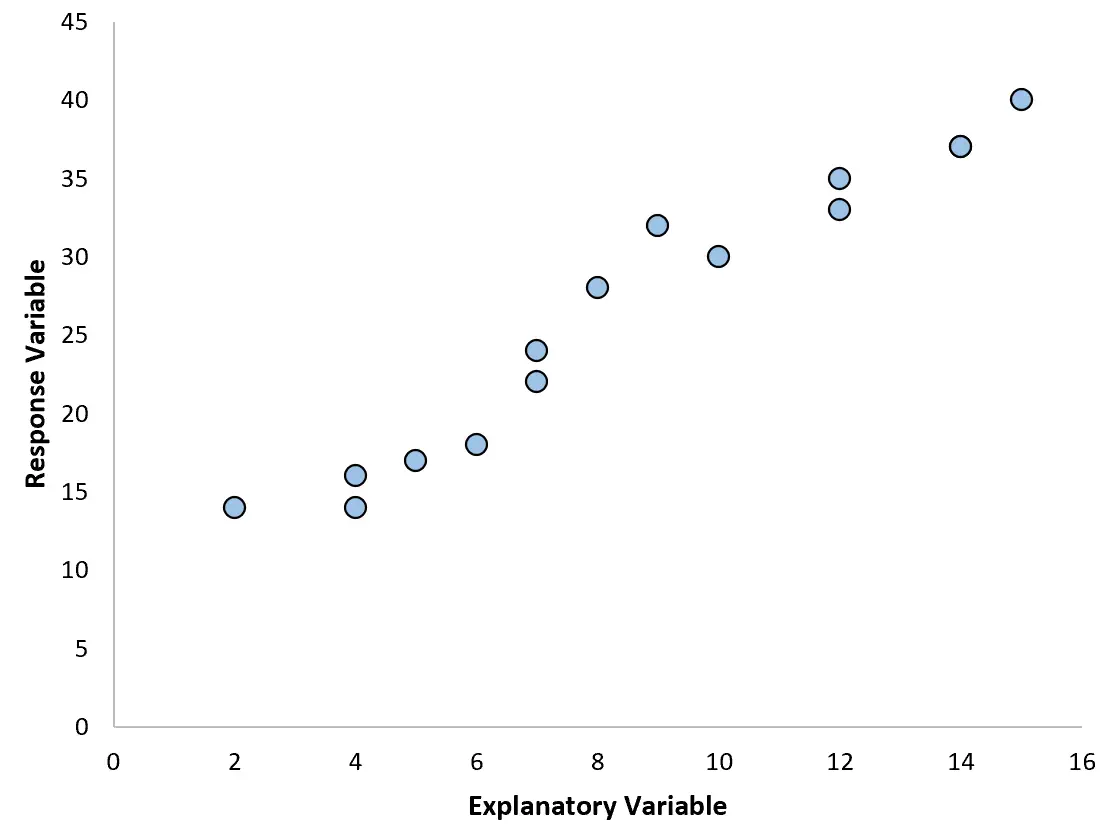
ただし、予測変数と応答変数の間の関係が非線形になる場合があります。
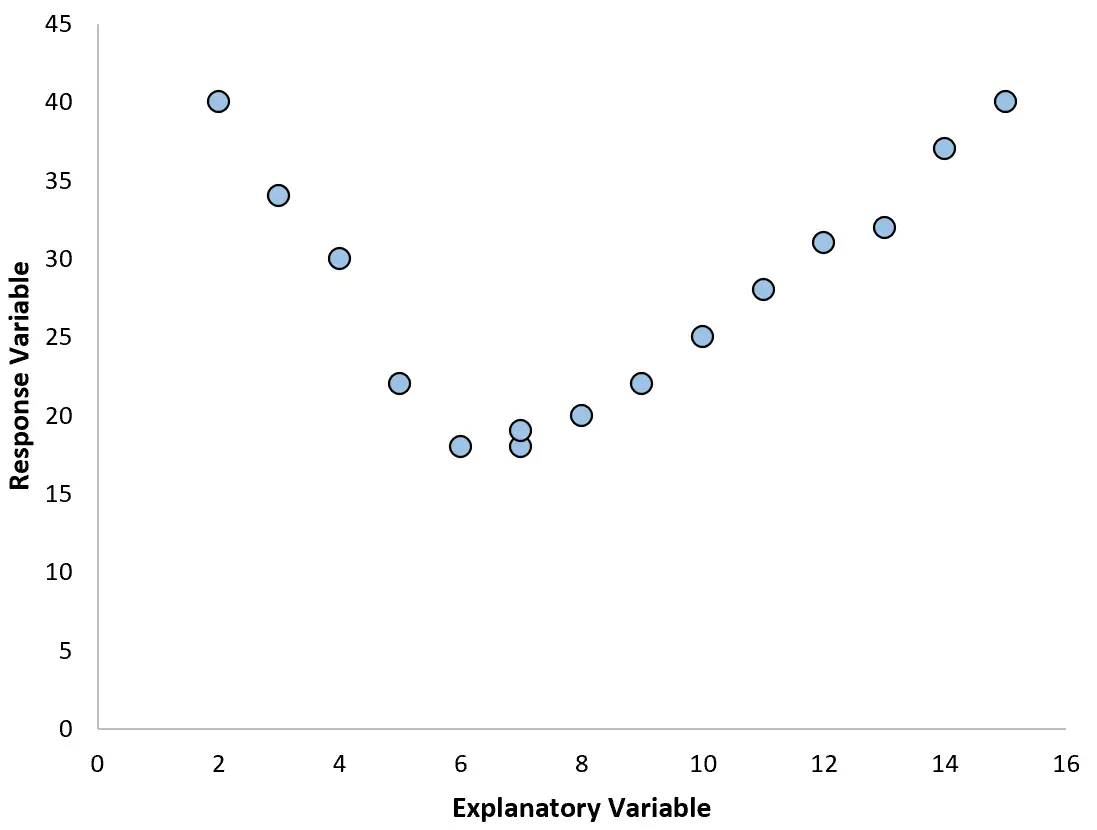
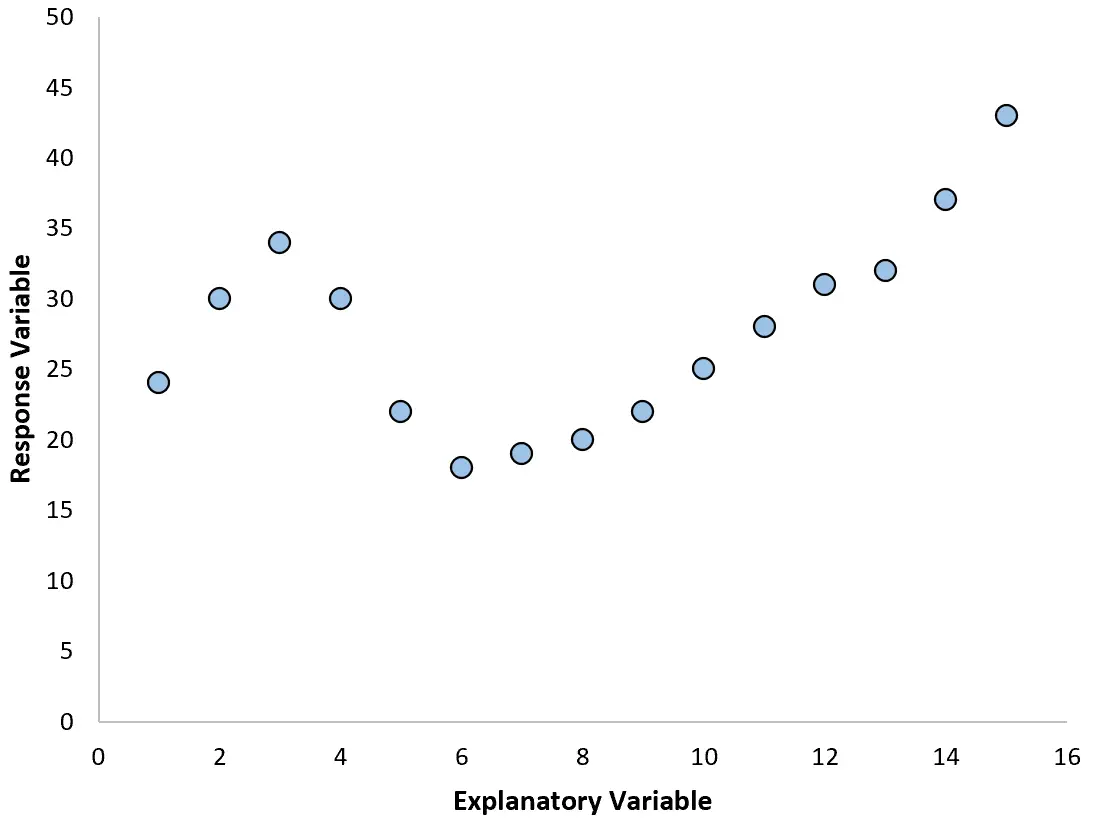
このような場合、変数間の非線形関係を説明できる多項式回帰を使用することが合理的です。
このチュートリアルでは、Google スプレッドシートで多項式回帰を実行する方法を段階的に説明します。
ステップ 1: データを作成する
まず、次の値を使用して偽のデータセットを作成しましょう。
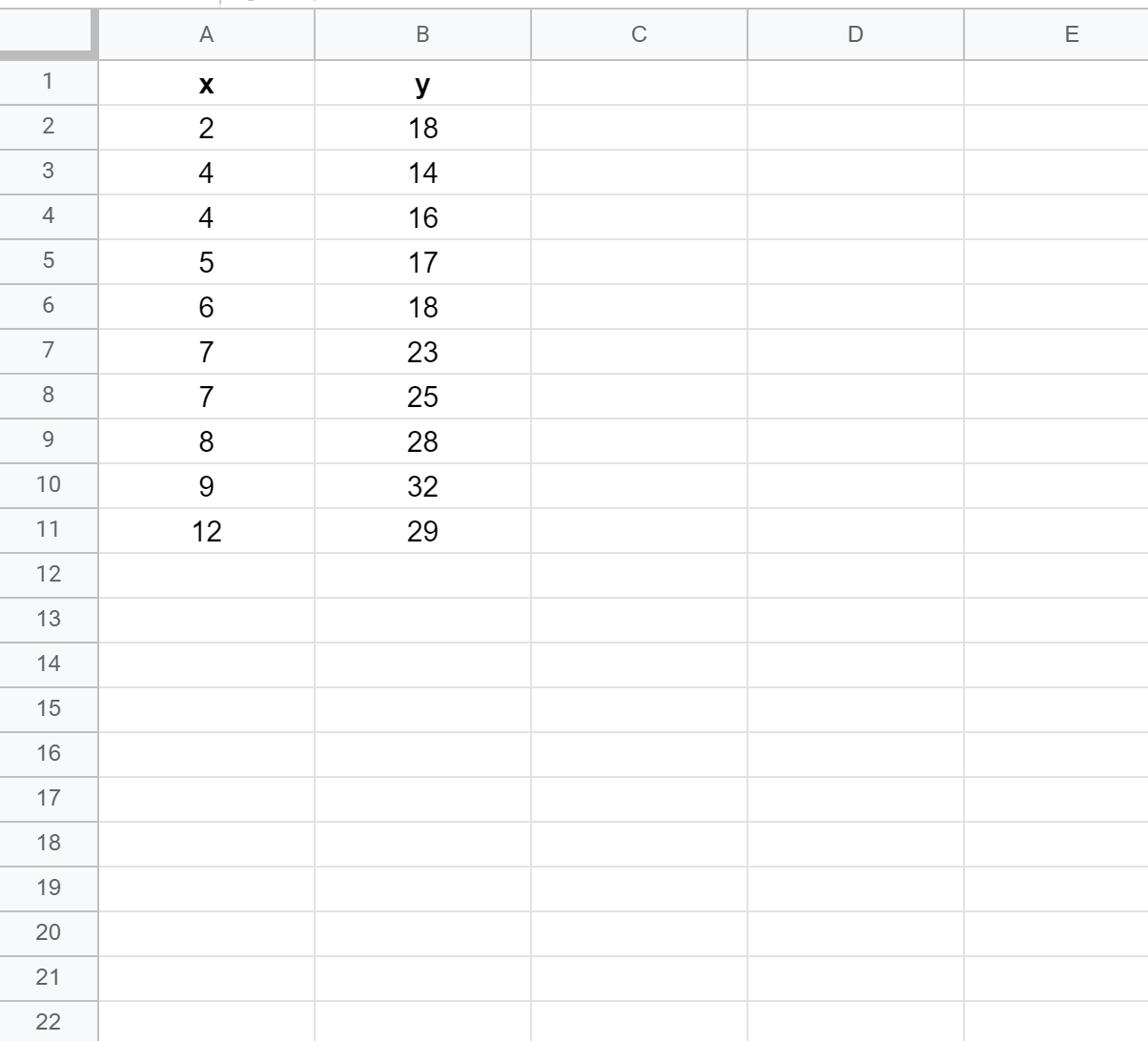
ステップ 2: 散布図を作成する
次に、データを視覚化するための散布図を作成します。
まず、次のようにセルA2:B11を強調表示します。
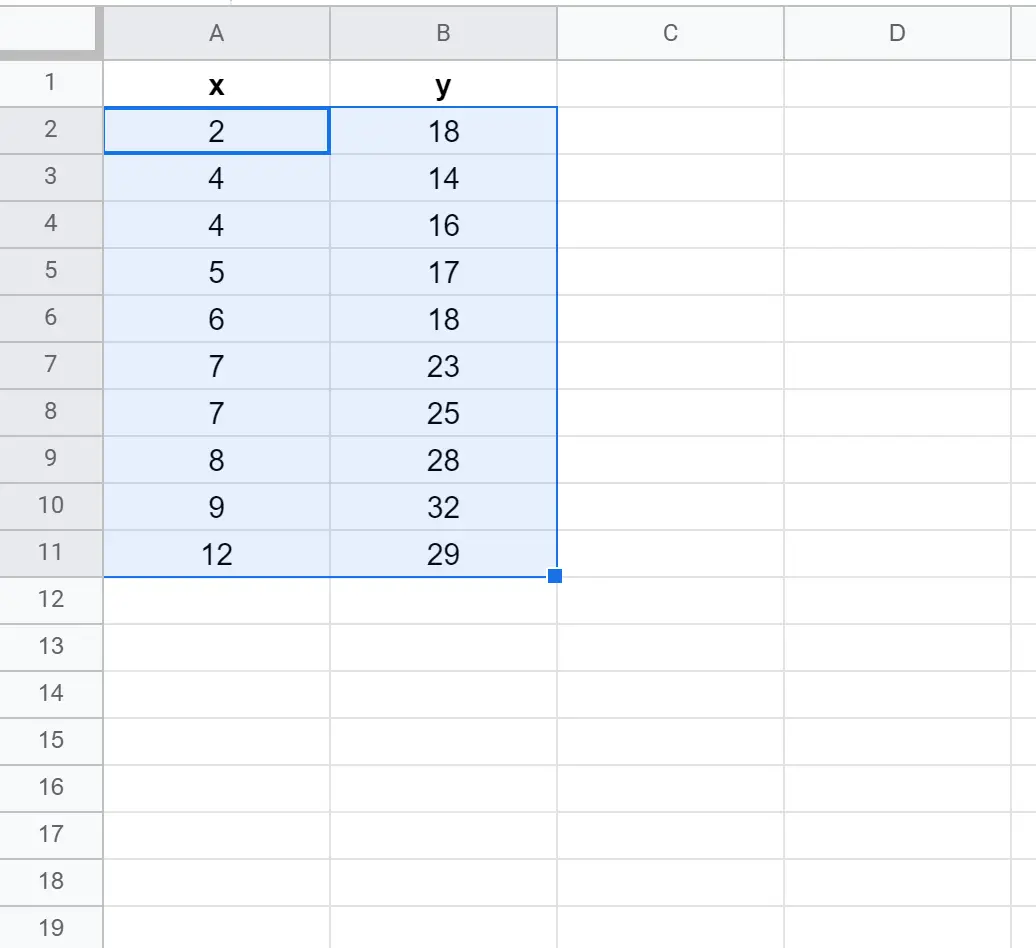
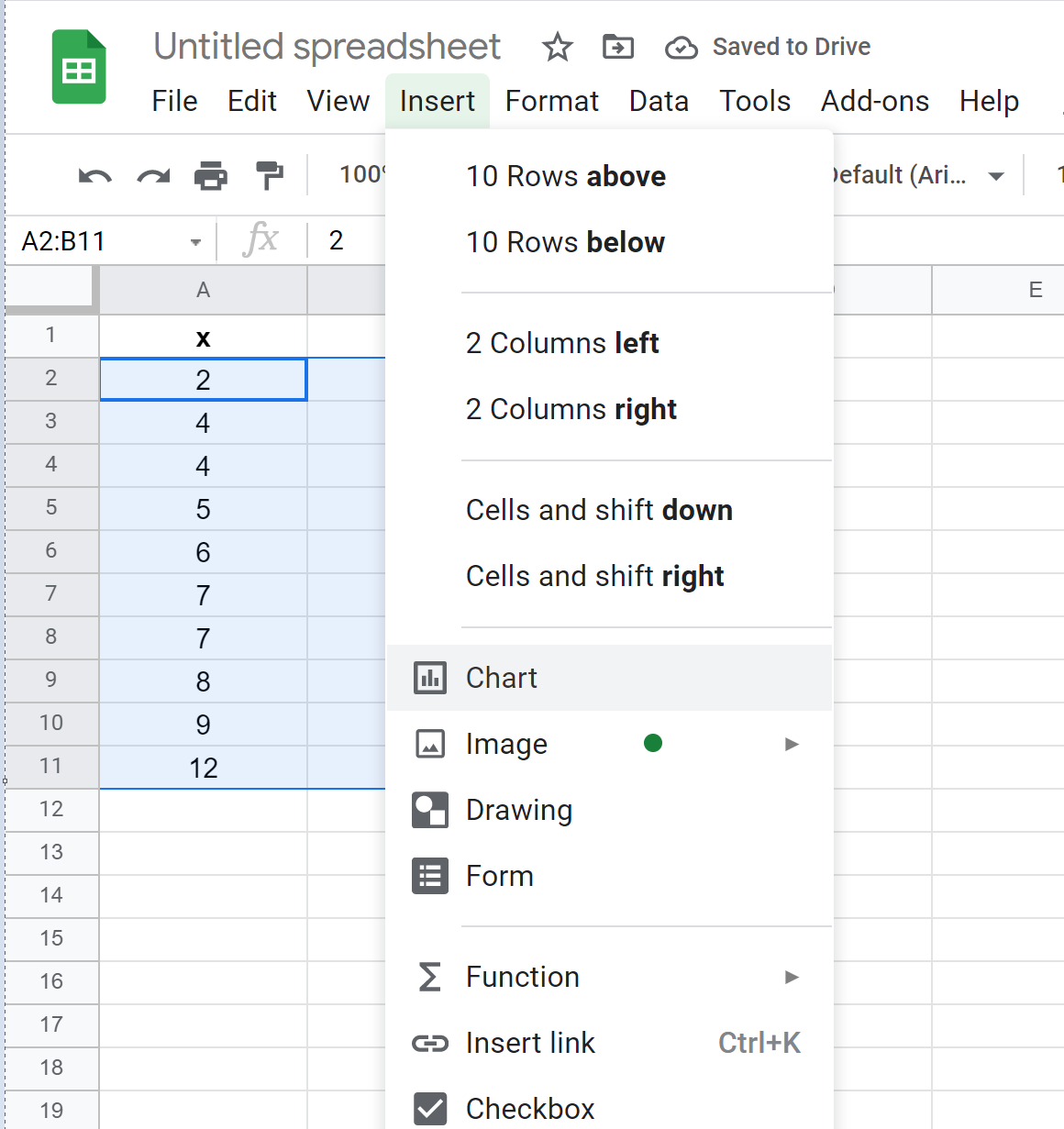
次に、 [挿入]タブをクリックし、ドロップダウン メニューから[グラフ]をクリックします。
デフォルトでは、Google スプレッドシートは散布図を挿入します。
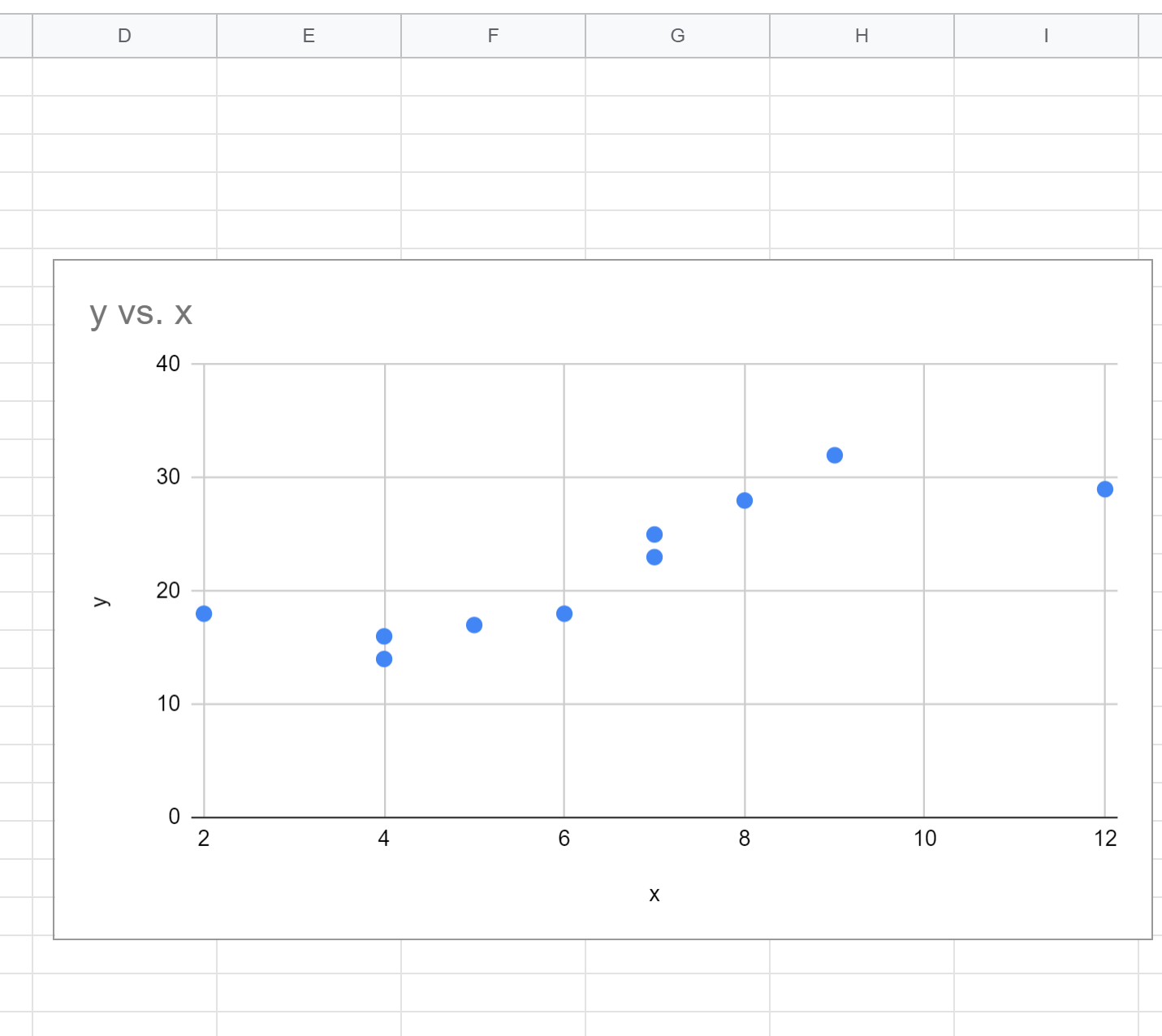
ステップ 3: 多項式回帰式を見つける
次に、散布図上の任意の場所をダブルクリックして、右側にグラフ エディタウィンドウを表示します。
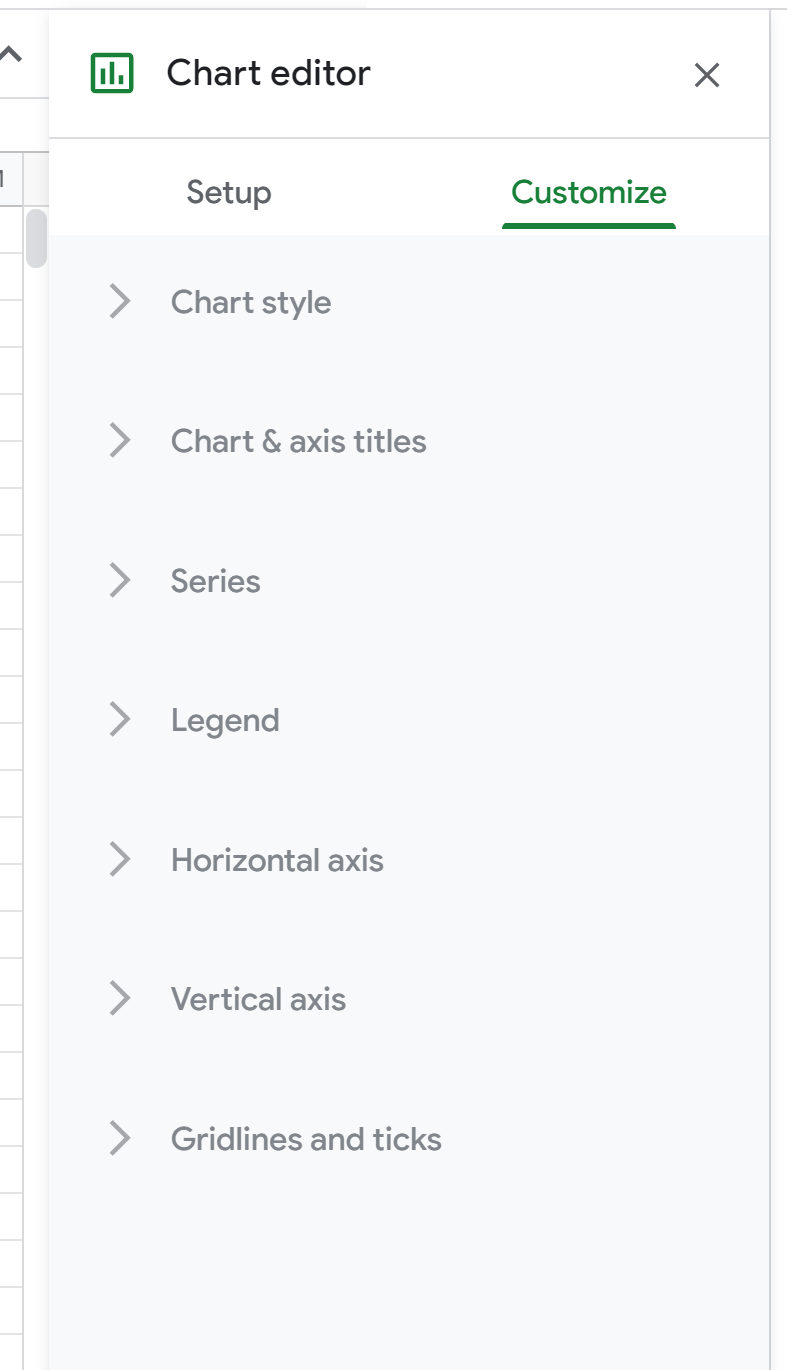
次に、 「シリーズ」をクリックします。次に、下にスクロールして[トレンドライン] の横のボックスをオンにし、[タイプ] を[多項式]に変更します。 [ラベル] で[方程式を使用]を選択し、 [R2を表示]の横のボックスをオンにします。
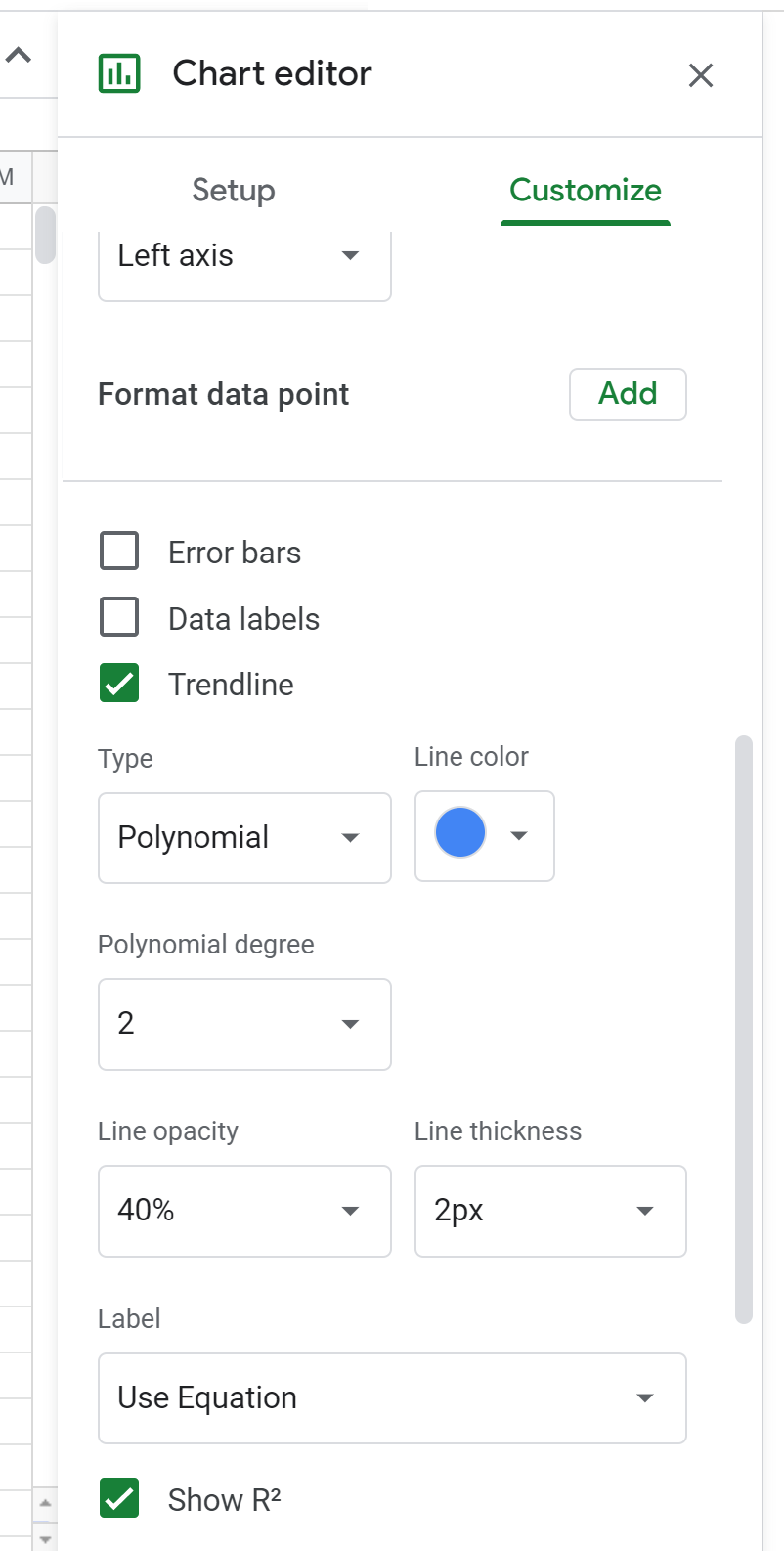
これにより、散布図の上に次の数式が表示されます。
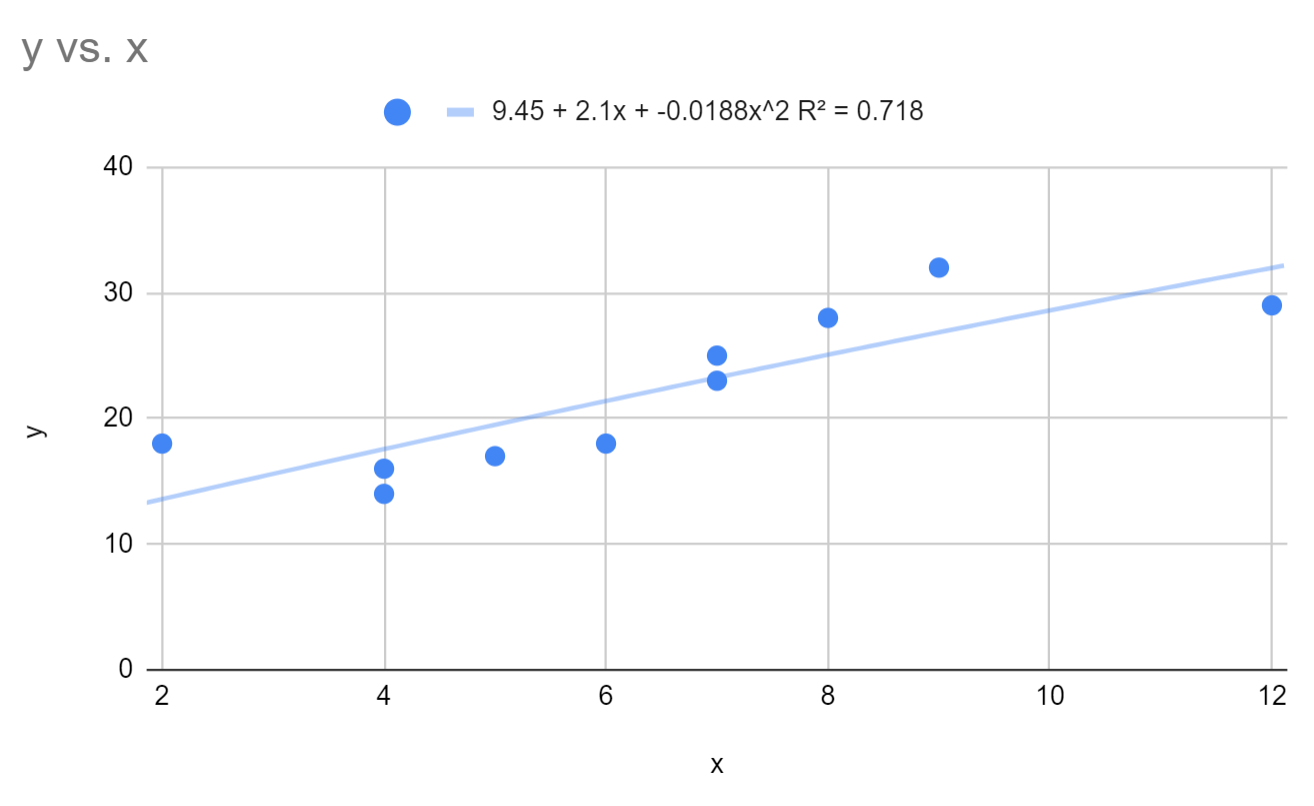
近似された多項式回帰式は次のとおりであることがわかります。
y = 9.45 + 2.1x – 0.0188x 2
このモデルの R 二乗は0.718です。
R 二乗は、予測変数によって説明できる応答変数の変動のパーセンテージを示していることを思い出してください。値が大きいほど、モデルは優れています。
次に、グラフエディタで多項式の次数を 3 に変更します。
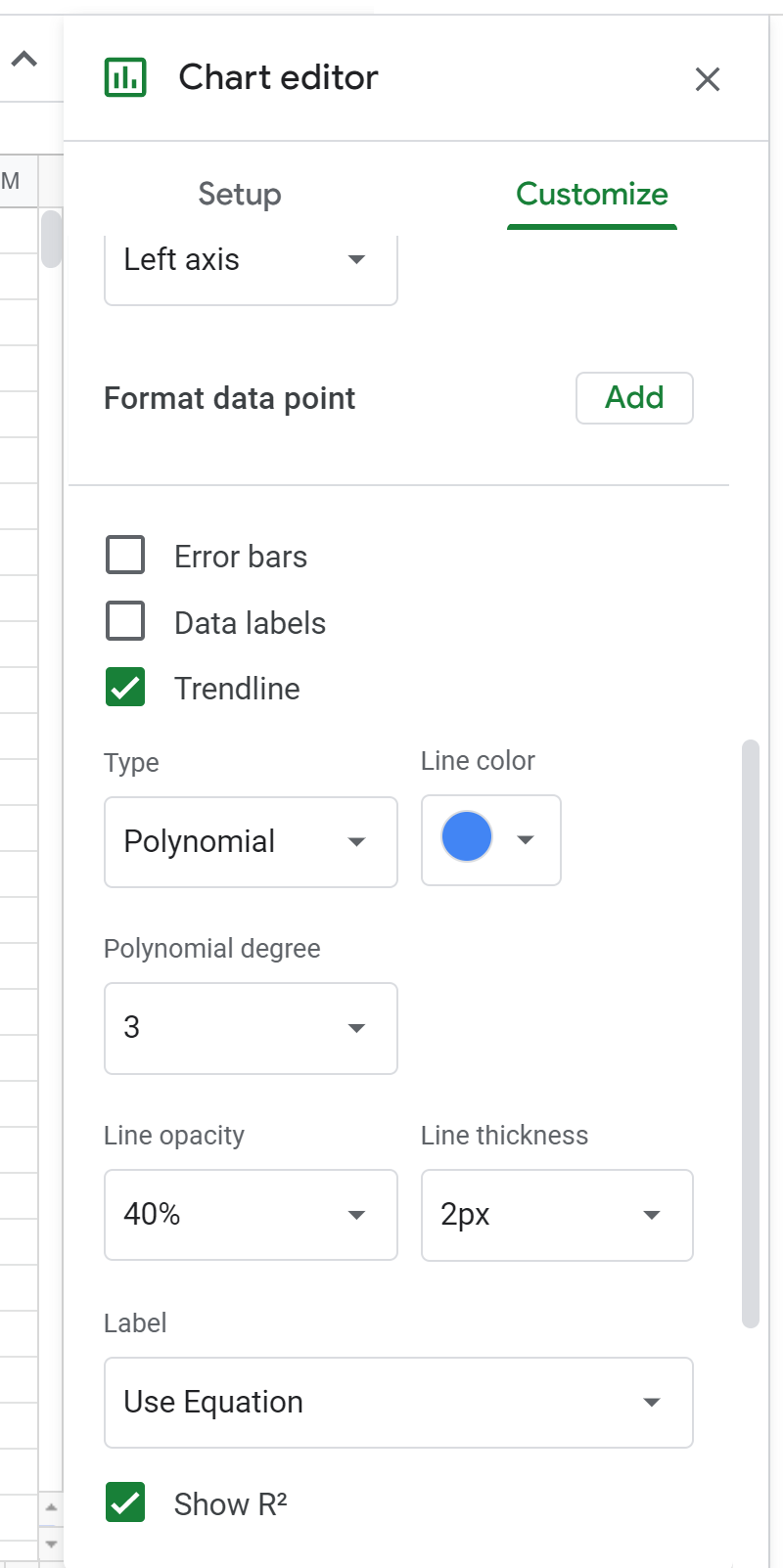
これにより、散布図の上に次の数式が表示されます。
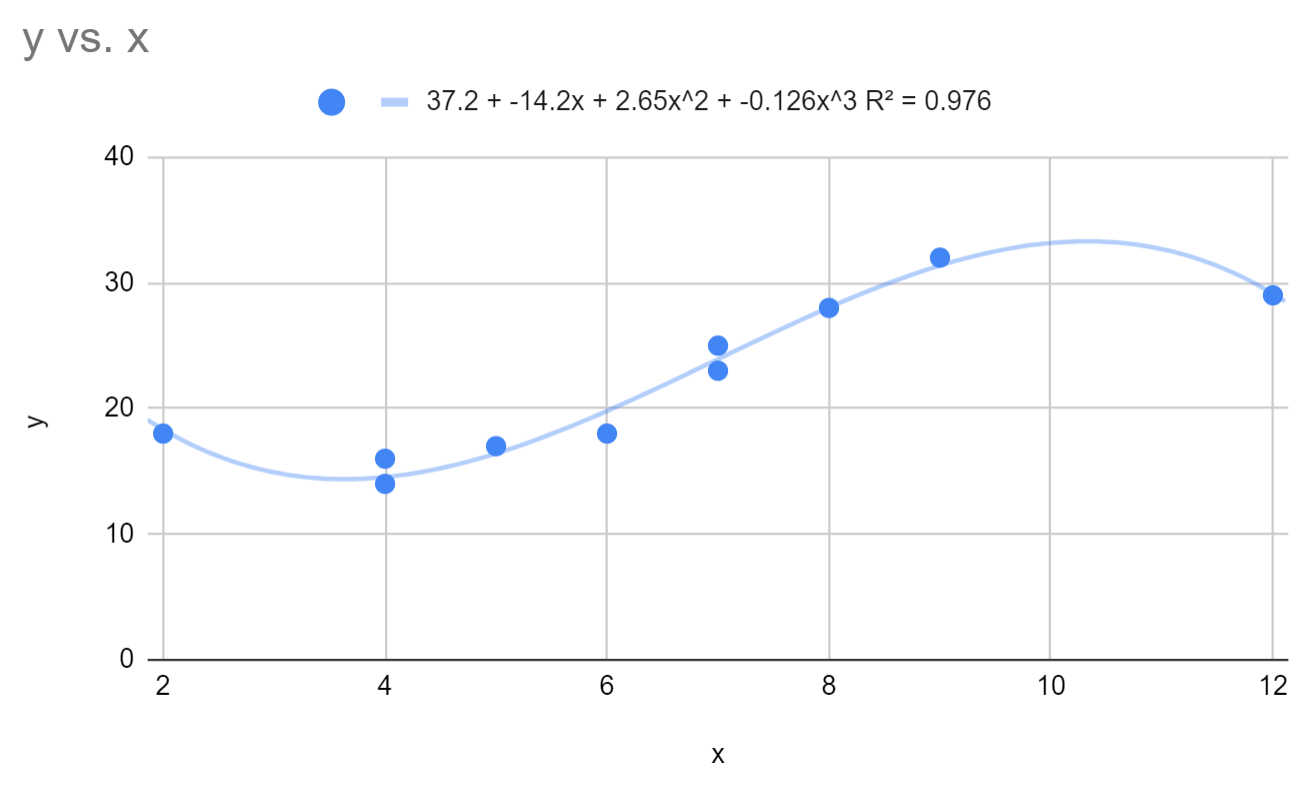
これにより、近似された多項式回帰式が次のように変更されます。
y = 37.2 – 14.2x + 2.64x 2 – 0.126x 3
このモデルの R 二乗は0.976です。
このモデルの R 二乗は、次数 2 の多項式回帰モデルの R 二乗よりも大幅に高いことに注意してください。これは、この回帰モデルが基礎となるデータの傾向を捉えるのに大幅に優れていることを示唆しています。
多項式の次数を 4 に変更すると、R 2 乗はわずかに0.981まで増加します。これは、これらのデータの傾向を捉えるには次数 3 の多項式回帰モデルで十分であることを示唆しています。
近似回帰式を使用して、予測変数の指定された値から応答変数の期待値を見つけることができます。たとえば、 x = 4 の場合、 yの期待値は次のようになります。
y = 37.2 – 14.2(4) + 2.64(4) 2 – 0.126(4) 3 = 14.576
このページでは、他の Google スプレッドシートのチュートリアルを見つけることができます。