密度関数
この記事では、密度関数とは何か、密度関数から確率を計算する方法、およびこの確率関数の特性について説明します。さらに、密度関数と分布関数の違いがわかるようになります。
密度関数とは何ですか?
密度関数 は、確率密度関数とも呼ばれ、連続確率変数が特定の値を取る確率を記述する数学関数です。
言い換えれば、変数に関連付けられた密度関数は、変数が値を取る確率を数学的に定義します。
たとえば、人口内で成人の身長が 1.80 m を超える確率が 35% であるとします。この確率を計算する際、密度関数は 35% の確率を示します。
確率密度関数は PDF と略される場合があります。
密度関数を使用して確率を計算する
連続変数が区間内で値を取る確率を求めるには、区間の限界間の前記変数に関連付けられた密度関数の積分を計算する必要があります。
![]()
金
![]()
は連続確率変数の密度関数です。
言い換えると、ある区間で変数が値を取る確率は、その区間の密度関数の下の面積に相当します。
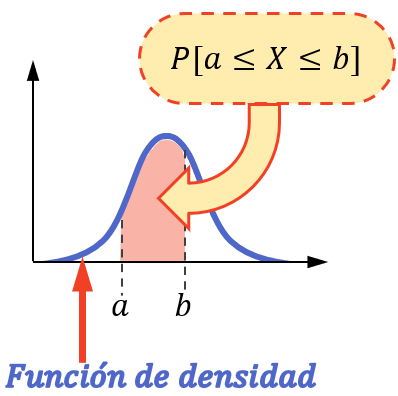
確率計算は、統計変数が正規分布、指数分布、ポアソン分布などの連続分布に従う場合にのみこの方法で実行できることに注意してください。
密度関数のプロパティ
密度関数には次の特性があります。
- 密度関数の値は、x の任意の値に対してゼロまたは正になります。
![]()
- さらに、密度関数の最大値は 1 に等しくなります。
![]()
- 実際、密度関数グラフの下の合計面積は、すべての確率のセットに対応するため、変数に関係なく常に 1 と等価です。
![]()
- 前のセクションで説明したように、連続変数が区間内で値を取る確率は、その区間内の密度関数の積分で計算されます。
![]()
密度関数と分布関数
この最後のセクションでは、密度関数と分布関数がどのように異なるかを見ていきます。これらは一般に混同されやすい 2 種類の確率関数であるためです。
数学的には、分布関数は密度関数の積分に相当するため、分布関数は連続変数の累積確率を表します。
つまり、任意の値の分布関数のイメージは、変数がその値またはそれより低い値を取る確率に等しくなります。
したがって、これら 2 種類の関数間の数学的関係は次のようになります。
![]()
金
![]()
は密度関数であり、
![]()
は分布関数です。
密度関数のグラフ表示が、平均 1、標準偏差 0.5 の正規分布に従う変数の分布関数と比較してどのように変化するかに注目してください。

配布機能の詳細については、以下のリンクをクリックしてください。