対応のあるサンプルの t 検定: 定義、公式、例
対のあるサンプルの t 検定は、一方のサンプルの各観測値がもう一方のサンプルの観測値と関連付けられる場合に、2 つのサンプルの平均を比較するために使用されます。
このチュートリアルでは次について説明します。
- 対応のあるサンプルの t 検定を実行する動機。
- 対応のあるサンプルの t 検定を実行するための式。
- 対応のあるサンプルの t 検定を実行するために満たさなければならない仮定。
- 対応のあるサンプルの t 検定を実行する方法の例。
対応のあるサンプルの t 検定: モチベーション
対応のあるサンプルの t 検定は、通常、次の 2 つのシナリオで使用されます。
1. 治療の前後に被験者の測定が行われます。たとえば、大学バスケットボール選手の最大垂直ジャンプは、トレーニング プログラムへの参加の前後に測定されます。
2. 測定は 2 つの異なる条件下で行われます。たとえば、患者の反応時間を 2 つの異なる薬剤で測定します。
どちらの場合も、一方のサンプルからの各観測値をもう一方のサンプルからの観測値と関連付けることができる 2 つのグループ間の平均測定値を比較したいと考えています。
対応のあるサンプルの t 検定:式
対応のあるサンプルの t 検定では、常に次の帰無仮説が使用されます。
- H 0 : μ 1 = μ 2 (2 つの母集団平均は等しい)
対立仮説は、左または右の両側に存在する可能性があります。
- H 1 (両側): μ 1 ≠ μ 2 (2 つの母集団の平均は等しくない)
- H 1 (左): μ 1 < μ 2 (母集団 1 の平均は母集団 2 の平均より低い)
- H 1 (右): μ 1 > μ 2 (母集団 1 の平均は母集団 2 の平均より大きい)
次の式を使用して t 検定統計量を計算します。
t = x diff / (s diff /√n)
金:
- x diff :差の平均の例
- s:差の標準偏差の例
- n:サンプルサイズ (つまり、ペアの数)
(n-1) 自由度の t 検定統計量に対応する p 値が、選択した有意水準 (一般的な選択肢は 0.10、0.05、および 0.01) より小さい場合、帰無仮説を棄却できます。
対応のあるサンプルの t 検定: 仮定
対応のあるサンプルの t 検定の結果が有効であるためには、次の前提を満たす必要があります。
- 参加者は母集団からランダムに選択する必要があります。
- ペア間の差はほぼ正規分布する必要があります。
- 差異に極端な外れ値があってはなりません。
対応のあるサンプルの t 検定: 例
特定のトレーニング プログラムが大学バスケットボール選手の最大垂直ジャンプ (インチ単位) を向上させることができるかどうかを知りたいとします。
これをテストするために、20 人の大学バスケットボール選手の 単純なランダム サンプルを採用し、それぞれの最大垂直ジャンプを測定できます。次に、各プレーヤーにトレーニング プログラムを 1 か月間使用してもらい、月末に最大垂直跳びを再度測定します。

トレーニング プログラムが実際に最大垂直ジャンプに影響を与えたかどうかを判断するには、次の手順を使用して、α = 0.05 の有意水準で一対のサンプルの t 検定を実行します。
ステップ 1: 差異の要約データを計算します。
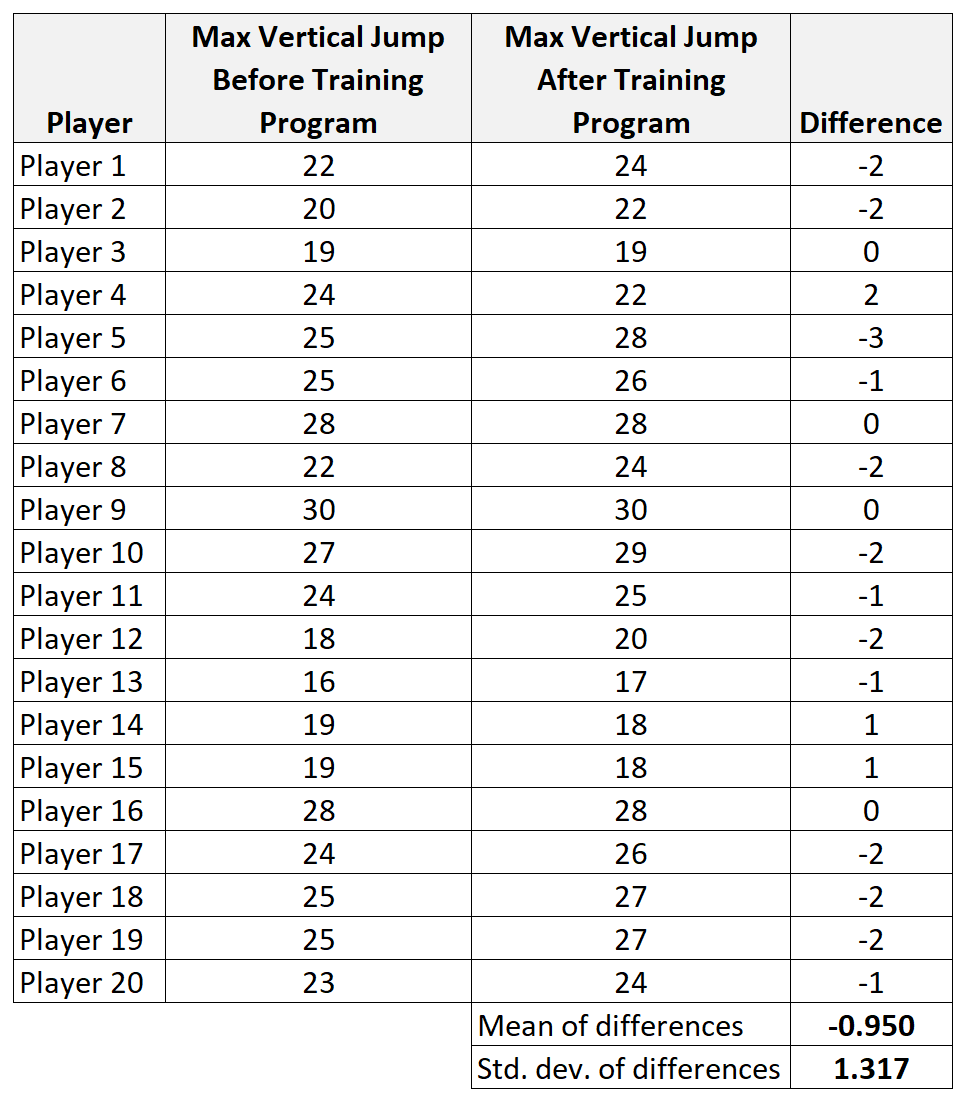
- x diff :差のサンプル平均 = -0.95
- s:差異のサンプル標準偏差 = 1.317
- n:サンプルサイズ (ペアの数) = 20
ステップ 2: 前提条件を定義します。
次の仮説を使用して、対応のあるサンプルの t 検定を実行します。
- H 0 : μ 1 = μ 2 (2 つの母集団平均は等しい)
- H 1 : μ 1 ≠ μ 2 (2 つの母集団平均は等しくない)
ステップ 3: t検定統計量を計算します。
t = x差分/ (s差分/√n) = -0.95 / (1.317/ √ 20) = -3.226
ステップ 4: t検定統計量の p 値を計算します。
P 値に対する T スコアの計算ツールによると、t = -3.226 および自由度 = n-1 = 20-1 = 19 に関連付けられた p 値は0.00445です。
ステップ 5: 結論を導き出します。
この p 値は有意水準 α = 0.05 を下回っているため、帰無仮説を棄却します。トレーニングプログラムに参加する前と後で、プレーヤーの平均最大垂直ジャンプが異なると言える十分な証拠があります。
注:対サンプル t 検定計算機を使用するだけで、この対サンプル t検定全体を実行することもできます。
追加リソース
次のチュートリアルでは、さまざまな統計プログラムを使用して、対応のあるサンプルの t 検定を実行する方法を説明します。
Excel で対応のあるサンプルの t 検定を実行する方法
SPSS で対応のあるサンプルの t 検定を実行する方法
Stata で対応のあるサンプルの t 検定を実行する方法
TI-84 電卓で対応のあるサンプルの t 検定を実行する方法
R で対応のあるサンプルの t 検定を実行する方法
Python で対応のあるサンプルの t 検定を実行する方法
対応のあるサンプルの T 検定を手動で実行する方法