対称分布
この記事では、対称分布とは何か、対称分布の例、分布が対称か非対称かを判断する方法について学びます。
対称分布とは何ですか?
統計において、対称分布とは、平均の左側と右側の値の数が同じである分布のことです。言い換えれば、対称分布では、平均が対称軸になります。
たとえば、正規分布は対称分布です。
すべての対称分布では、平均値は中央値と等しくなります。しかし、分布が単峰性である場合 (統計的最頻値が単一の値である場合)、平均、中央値、および最頻値は等価になります。
論理的には、対称分布とは何かを完全に理解するには、平均、中央値、最頻値が何であるかを明確にする必要があります。これらの統計概念の意味をここで確認できます。
対称分布の例
対称分布の定義を考慮して、このタイプの分布の例を以下に示します。
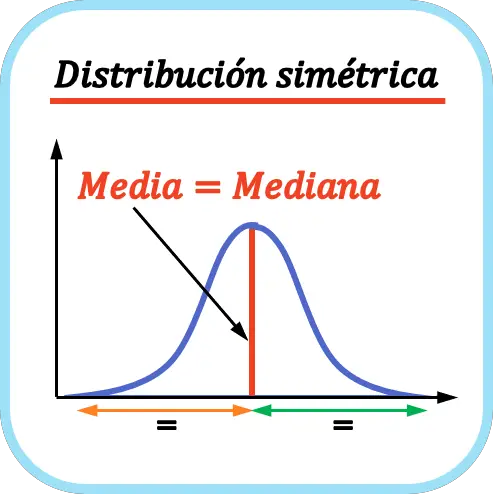
グラフが示すように、平均はすべてのデータのちょうど中央に位置するため、分布は対称的です。つまり、曲線の左側の裾は右側の裾と同じです。この場合、モードは単峰性であるため、平均、中央値、および最頻値は同じになります。
2 つの異なるタイプの対称確率分布の 2 つの明確な例は、正規分布と一様分布です。これは、これらは平均の左右に同じ数の値があるためです。
一方、分布は対称かつ二峰性、つまり 2 つのモードを持つこともあります。次の例を見てください。
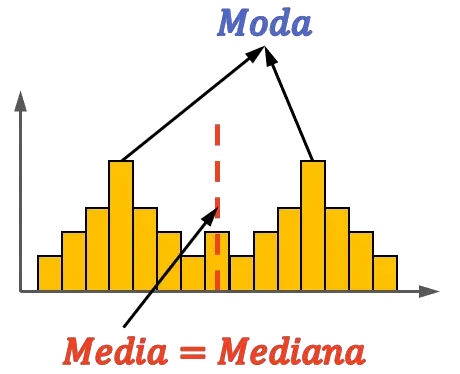
この他の例でわかるように、二峰性分布は他の値に関係なく中央に平均値と中央値を持つことができるため、対称になることもあります。ただし、この場合、最頻値は必ずしも平均値と最頻値に等しい必要はありません。
対称性に基づく他のタイプの分布
対称分布の他に、他に 2 つのタイプの非対称分布があります。
- 対称分布: 分布は平均値の左右に同じ数の値を持ちます。
- 正に歪んだ分布: 分布には、平均の左側より右側の方が異なる値が多くあります。
- 負に歪んだ分布: 分布には、平均の右側よりも左側の方が異なる値が多くあります。

分布が対称かどうかを確認する方法
分布が対称かどうかを判断するには、ピアソンの非対称係数を計算する必要があります。その式は次のとおりです。
![]()
金
![]()
はピアソン係数、
![]()
算術平均、
![]()
モード (統計) と
![]()
標準偏差。
したがって、ピアソン非対称係数の符号に応じて、分布は対称または非対称になります。
- ピアソンの歪度係数が正の場合、分布が正に歪んでいることを意味します。
- ピアソンの歪度係数が負の場合、分布が負に歪んでいることを意味します。
- ピアソンの歪度係数がゼロの場合、分布が対称であることを意味します。
ただし、ピアソン係数は、分布が単峰性の場合にのみ計算できます。それ以外の場合は、式が次のようなフィッシャーの非対称係数を使用する必要があります。

金
![]()
算術平均、
![]()
標準偏差と
![]()
データの総数。
フィッシャーの非対称係数の解釈はピアソン係数と同じです。値が正の場合は分布が正の非対称であることを意味し、負の場合は分布が負の非対称であることを意味し、ゼロの場合は分布が対称であることを意味します。