平均と標準偏差から確率を求める方法
次のプロセスを使用して、正規分布確率変数が存在する確率を見つけることができます。
ステップ 1: Z スコアを見つけます。
Z スコアは、個々のデータ値が平均からどれだけ標準偏差離れているかを示します。次のように計算されます。
z スコア = (x – μ) / σ
金:
- x:個別のデータ値
- μ:母集団平均
- σ:母集団標準偏差
ステップ 2: Z スコアに対応する確率を見つけます。
Z スコアを計算したら、それに対応する確率を Z テーブルで見つけることができます。
次の例は、さまざまなシナリオでこのプロセスを使用する方法を示しています。
例 1: 一定の値未満の確率
特定のテストのスコアは、平均 μ = 82、標準偏差 σ = 8 で正規分布します。特定の生徒のテストのスコアが 84 未満である確率はどれくらいですか?
ステップ 1: Z スコアを見つけます。
まず、スコア 84 に関連付けられた Z スコアを見つけます。
z スコア = (x – μ) / σ = (84 – 82) / 8 = 2/8 = 0.25
ステップ 2: Z テーブルを使用して、対応する確率を見つけます。
次に、z テーブルで値0.25を探します。

特定の生徒の得点が 84 点未満になる確率は約59.87%です。
例 2: 特定の値より大きい確率
特定の種のペンギンの身長は、平均 μ = 30 インチ、標準偏差 σ = 4 インチで正規分布します。ペンギンをランダムに選択した場合、そのペンギンの身長が 28 インチを超える確率はどれくらいですか?
ステップ 1: Z スコアを見つけます。
まず、高さ 28 インチに関連付けられた Z スコアを見つけます。
スコア z = (x – μ) / σ = (28 – 30) / 4 = -2 / 4 = -0.5
ステップ 2: Z テーブルを使用して、対応する確率を見つけます。
次に、値-0.5を探します。 表z:
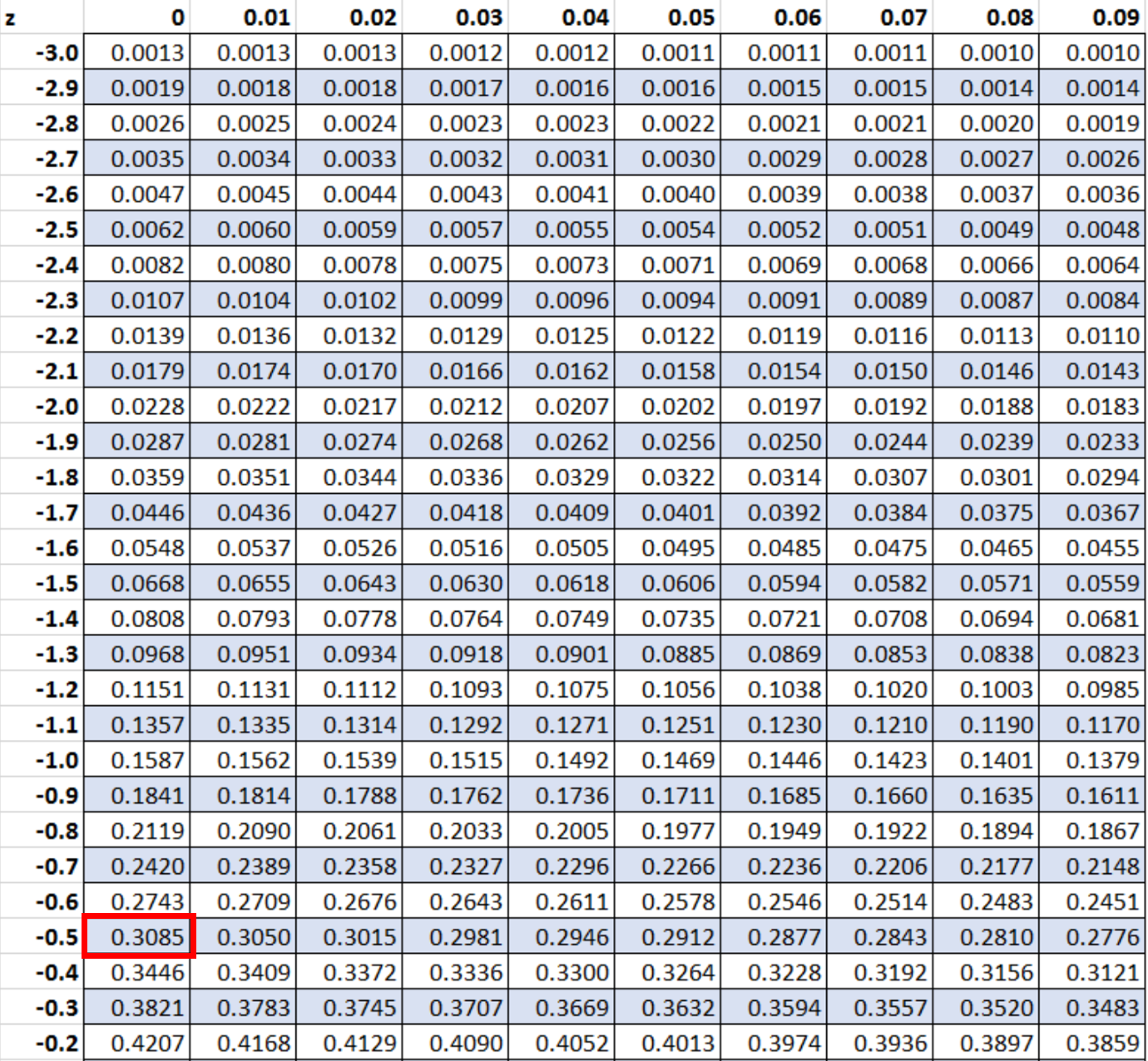
Z スコア -0.5 に対応する値は 0.3085 です。これは、ペンギンの身長が 28 インチ未満になる確率を表します。
ただし、ペンギンの身長が 28 インチを超える確率を知りたいので、その確率を 1 から引く必要があります。
したがって、ペンギンの身長が 28 インチを超える確率は、 1 – 0.3085 = 0.6915となります。
例 3: 2 つの値の間の確率
特定の種類のカメの体重は、平均 μ = 400 ポンド、標準偏差 σ = 25 ポンドで正規分布します。カメをランダムに選択した場合、その体重が 410 ポンドから 425 ポンドの間である確率はどれくらいですか?
ステップ 1: Z スコアを見つけます。
まず、410 冊と 425 冊の書籍に関連付けられた Z スコアを見つけます。
410 の Z スコア = (x – μ) / σ = (410 – 400) / 25 = 10/25 = 0.4
z スコア 425 = (x – μ) / σ = (425 – 400) / 25 = 25 / 25 = 1
ステップ 2: Z テーブルを使用して、対応する確率を見つけます。
まず、値0.4を探します。 表z:

次に値1を探します。 表z:

次に、大きい値から小さい値を引きます: 0.8413 – 0.6554 = 0.1859 。
したがって、ランダムに選択されたカメの体重が 410 ポンドから 425 ポンドの間である確率は18.59%です。