平均値の差の標本分布
この記事では、統計における 2 つの平均の差の標本分布がどのようなものになるかについて説明します。また、平均値の差の標本分布の公式と、段階的に解決される演習も見つかります。
平均値の差の標本分布はどのようなものですか?
平均値の差の標本分布は、 2 つの異なる母集団から得られるすべてのサンプルの平均値間の差を計算して得られる分布です。
つまり、平均値の差の標本分布を取得するには、2 つの研究母集団から考えられるすべてのサンプルを選択し、選択した各サンプルの平均値を計算し、最後に 2 つの母集団からすべての平均値の差を計算する必要があります。したがって、これらすべての操作を適用した後に得られる一連の値は、平均値の差の標本分布を形成します。

平均値の標本分布の差は、2 つの異なる母集団からランダムに選択されたサンプルの 2 つの平均値の差が母集団の平均値の差に近い確率を計算するために使用されます。
平均値の差の標本分布の公式
サンプルサイズが十分に大きい場合(n 1 ≧ 30 および n 2 ≧ 30)、平均値の差の標本分布は正規分布に従います。より正確には、前記分布のパラメータは次のように計算されます。
![Rendered by QuickLaTeX.com \begin{array}{c}\displaystyle \mu_{\overline{x_1}-\overline{x_2}}=\mu_1-\mu_2 \qquad \sigma_{\overline{x_1}-\overline{x_2}}=\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}\\[6ex]\displaystyle N_{\overline{x_1}-\overline{x_2}}\left(\mu_1-\mu_2, \sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}\right) \end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-90c67b74b4e9326b7869d641a59725d9_l3.png)
注:両方の母集団が正規分布である場合、平均値の差の標本分布はサンプル サイズに関係なく正規分布に従います。
したがって、平均値の差の標本分布は正規分布で定義されるため、平均値の差の標本分布の統計量を計算する式は次のようになります。

金:
-

はサンプル i の平均です。
-

は母集団 i の平均です。
-

は母集団 i の標準偏差です。
-

はサンプルサイズ i です。
-

は、標準正規分布 N(0,1) によって定義される変数です。
異なる母集団からのサンプルは異なるサンプルサイズを持つ可能性があることに注意してください。
平均値の差の標本分布の具体例
平均標本分布の差の定義とその式が何であるかを理解したら、ステップバイステップの例を見て、平均標本分布の差の概念の理解を完了します。
- 統計研究では、特定の年齢の男子と女子の身長の差を分析したいと考えています。この年齢の男の子の人口を定義する分布の平均は 157 cm、標準偏差は 9 cm であり、一方、この年齢の女の子の人口を定義する分布の平均は 148 cm であることがわかっています。 cm、標準偏差は7 cmです。この年齢の 30 人の男子のサンプルと 35 人の女子のサンプルを選択した場合、男子のサンプルの平均身長が女子のサンプルの平均身長より 12 cm 大きい確率はどれくらいですか?
この問題を解決するために、最初に行うことは、平均標本分布の差の統計量を計算することです。したがって、上記の式を適用します。
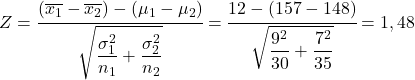
したがって、少年のサンプルの平均身長が少女の平均身長より 12 cm 大きい確率は、Z 変数が 1.48 より大きい確率と同等です。
![P[(\overline{x_1}-\overline{x_2})>12]=P[Z>1,48]” title=”Rendered by QuickLaTeX.com” height=”19″ width=”253″ style=”vertical-align: -5px;”></p>
</p>
<p>したがって、 <a href=](https://statorials.org/wp-content/ql-cache/quicklatex.com-683cd2a72980115d8d18c906d619370a_l3.png) Z の表で Z>1.48 の確率を探します。
Z の表で Z>1.48 の確率を探します。
![P[(\overline{x_1}-\overline{x_2})>12]=P[Z>1,48]=0,0694″ title=”Rendered by QuickLaTeX.com” height=”19″ width=”331″ style=”vertical-align: -5px;”></p>
</p>
<p>つまり、サンプルの男子の平均身長が女子の平均身長より 12 cm 大きい確率は 6.94% です。</p>
</div><!-- End Content -->
<!-- Start Author Box -->
<div class=](https://statorials.org/wp-content/ql-cache/quicklatex.com-5b83fdc11bd2320249679c4752660451_l3.png)
著者について
ベンジャミン・アンダーソン博士
私はベンジャミンです。退職した統計教授から、専任の Statorials 教育者になりました。 統計分野における豊富な経験と専門知識を活かして、私は Statorials を通じて学生に力を与えるために自分の知識を共有することに尽力しています。もっと知る