平均と標準偏差の関係 (例付き)

平均は、一連のデータの平均値を表します。

次のように計算されます。

サンプル平均 = Σx _i / n

金：

• Σ： 「和」を意味する記号
• x _i :データセット内の i^番目の観測値
• n:データセット内の観測値の総数

標準偏差は、平均に対するデータセット内の値の分布を表します。

次のように計算されます。

サンプル標準偏差 = √ Σ(x _i – x _bar ) ² / (n-1)

金：

• Σ： 「和」を意味する記号
• x _i :サンプルの^{i 番目}の値
• x _bar :サンプルの平均値
• n:サンプルサイズ

平均と標準偏差の関係に注目してください。平均は、標準偏差を計算するための式で使用されます。

実際、サンプルの平均値が分からない限り、サンプルの標準偏差を計算することはできません。

次の例は、実際にデータセットのサンプル平均とサンプル標準偏差を計算する方法を示しています。

例: データセットの平均と標準偏差の計算

10 人の異なるバスケットボール選手が獲得したポイントを示す次のデータセットがあるとします。

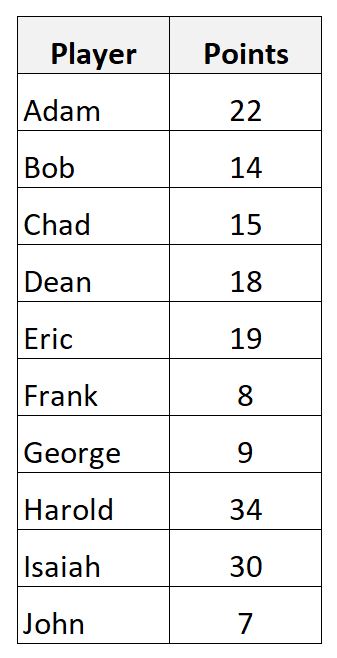次の式を使用して、得点のサンプル平均を計算できます。

• サンプル平均 = Σx _i / n
• サンプル平均 = (22+14+15+18+19+8+9+34+30+7) / 10
• サンプル平均 = 17.6

得点のサンプル平均は17.6です。これは、全プレイヤーが獲得した平均ポイント数を表します。

サンプルの平均値がわかったら、それを式に代入してサンプルの標準偏差を計算します。

• サンプル標準偏差 = √ Σ(x _i – x _bar ) ² / (n-1)
• サンプル標準偏差 = √ ((22-17.6) ² + (14-17.6) ² + (15-17.6) ² + (18-17.6) ² + (19-17.6) 6) ² + (8-17.6) ² + (9 -17.6) ² + (34-17.6) ² + (30-17.6) ² + (7-17.6) ² ) / (10-1)
• サンプル標準偏差 = 9.08

サンプルの標準偏差は9.08です。これは、各ポイント値とサンプル ポイント平均間の平均距離を表します。

各メトリクスから異なる情報が得られるため、データセットの平均と標準偏差の両方を知ることは役に立ちます。

平均値により、データセットの「中心」値がどこにあるかがわかります。

標準偏差は、データセット内の平均値付近の値の分布を把握します。標準偏差値が高いほど、サンプル内での値の分散が大きくなります。

これら 2 つの値を知ることで、データセット内の値の分布について多くのことを学ぶことができます。

追加リソース

次のチュートリアルでは、平均偏差と標準偏差に関する追加情報を提供します。

統計において平均が重要なのはなぜですか?
統計において標準偏差が重要なのはなぜですか?
Excel で平均偏差と標準偏差を計算する方法