幾何学的平均
この記事では、幾何平均とは何か、その計算方法、および幾何平均と算術平均の違いについて説明します。また、幾何平均の演習を段階的に解決し、このタイプの平均の特性を確認することもできます。最後に、任意のデータセットの幾何平均を計算する計算機を見つけます。
幾何平均とは何ですか?
幾何平均は、記述統計の中心性の尺度です。一連の統計データの幾何平均は、すべての値の積の n 乗根に等しくなります。
幾何平均は、ビジネス ファイナンスで収益率、平均パーセンテージ、複利を計算するために使用されます。
したがって、幾何平均の公式は次のようになります。

幾何平均は、サンプル内のすべてのデータが正の場合にのみ計算できます。値が負の場合、ルートには負の解が存在するか、解が存在しないことになるため、一方、データがゼロの場合、データの乗算はゼロになるため、幾何平均は 0 に等しくなります。
存在する平均の種類は幾何平均だけではありません。算術平均、加重平均、二乗平均、調和平均もあります。
幾何平均と算術平均の違い
幾何平均と算術平均の主な違いは、幾何平均は算術平均よりも極値の影響を受けにくいことです。さらに、算術平均は負の値とゼロの値を使用して計算できますが、幾何平均は正の値を使用してのみ計算できます。
同様に、幾何平均は通常、同じデータセットの算術平均よりも低くなります。
幾何平均の計算はより複雑であるため、その統計的有意性の解釈がより困難であることにも注意してください。
つまり、幾何平均には算術平均と比較して長所と短所があり、データの性質に応じて、さまざまな平均を計算することが適切になります。
幾何平均の計算方法
幾何平均を計算するには、次の手順を実行する必要があります。
- サンプル内のすべての統計データの積を計算します。
- 計算された積の n 乗根を求めます。
- 得られる結果は、統計サンプルの幾何平均です。
ご覧のとおり、積と根を計算するだけで済むため、電卓やコンピューター プログラムを使用してデータ セットの幾何平均を求めることは比較的簡単です。逆に手で計算するのはかなり手間がかかります。
👉これが、以下の計算機を使用してデータセットの幾何平均を計算することをお勧めする理由です。
幾何平均の例
幾何平均に関する理論を理解したら、幾何平均を取得する方法を正確に理解できるように例を示します。
- 過去 5 年間の企業の経済的成果が判明しています。同社は初年度に 10% の経済的収益性を生み出し、2 年目に利益は 23% に達し、3 年目に得たお金は 16%、4 年目には 7% の経済的収益性を達成し、投資額は増加しました。 5 年目には 20% の収益となりました。すべてのパーセンテージの平均を計算するように求められます。
これまで見てきたように、パーセンテージの平均を計算するには、算術平均を使用するのではなく、幾何平均を使用して計算を行う必要があります。
したがって、幾何平均の公式を適用します。
![]()
そして、例の値を式に代入して計算を実行します。
![]()
データ ポイントが 5 つあるため、5 番目の根を計算していることに注意してください。
幾何平均の数値結果は 1.15 で、これは同社が毎年平均 15% の経済成長を経験したことを意味します。
すべての値が正であったため幾何平均を取得できましたが、パーセントが負であった場合は、データを整数部分を含む正の小数として数式に入力する必要があることに注意してください。ゼロに等しい。たとえば、-30% の成長は、式で 0.70 (1-0.3=0.7) と表現される必要があります。
幾何平均計算機
サンプル統計量を以下の計算機に入力して、幾何平均を求めます。データはスペースで区切られ、小数点としてピリオドを使用して入力する必要があります。値が負またはゼロの場合、幾何平均を求めることはできないことに注意してください。
幾何平均の性質
幾何平均には次の特徴があります。
- これは平均の一種で、パーセンテージやインデックスの平均を求めるのに非常に便利です。
- すべてのデータが正の場合にのみ計算できます。
- 2 つの数値aとbの幾何平均の幾何学的意味は、辺がaとbである長方形と同じ面積を持つ正方形の辺です。
![]()
- 3 つの数値a 、 b 、 cの幾何平均の幾何学的意味は、その体積が辺a 、 b 、 cの平行六面体に等しい立方体の辺です。
![]()
- データセットの幾何平均の対数は、同じセットの対数の算術平均を与えます。
- 一連の値の幾何平均は、常に算術平均以下になります。
![]()
- 加重幾何平均は幾何平均と同じ方法で計算されますが、各データ項目の指数に重みを追加して統計値に重みを付けます。
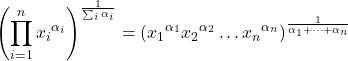
Excel で幾何平均を計算する
最後に、Excel プログラムを使用してデータセットの幾何平均を見つける方法を見てみましょう。
Excel で幾何平均を計算するには、 MEANS.GEOM 関数を使用する必要があります。幾何平均をとりたいすべての値を入力するだけで、関数は幾何平均の結果を返します。
たとえば、上記の例の幾何平均を求めるには、Excel ボックスに=MEDIA.GEOM(1.1;1.23;1.16;1.07;1.20) と記述する必要があります。
いずれかの値がゼロまたは負の場合、関数はエラーを返すことに注意してください。
ご覧のとおり、データをシートにコピーして数式を使用するだけなので、Excel で幾何平均を計算する方がはるかに簡単かつ高速です。