二元配置分散分析を手動で実行する方法

二元配置分散分析は、 2 つの因子に分割された 3 つ以上の独立したグループの平均間に統計的に有意な差があるかどうかを判断するために使用されます。

このチュートリアルでは、二元配置分散分析を手動で実行する方法について説明します。

例: 手動二元配置分散分析

植物学者が、日光への曝露や水やりの頻度が植物の成長に影響を与えるかどうかを知りたいとします。彼女は 40 個の種を植え、日光への曝露や水やりの頻度などのさまざまな条件で 1 か月間成長させます。

1 か月後、彼女は各植物の高さを記録します。結果を以下に示します。

上の表では、各条件の組み合わせで 5 つの植物が栽培されたことがわかります。

たとえば、5 つの植物を毎日水やり、日光を当てずに育てたところ、2 か月後の高さは 4.8 インチ、4.4 インチ、3.2 インチ、3.9 インチ、4.4 インチでした。

次の手順を使用して、二元配置分散分析を実行できます。

ステップ 1: 最初の要素 (水やりの頻度) の二乗和を計算します。

まず、40 個の植物の全体の平均高さを計算します。

全体の平均 = (4.8 + 5 + 6.4 + 6.3 + … + 3.9 + 4.8 + 5.5 + 5.5) / 40 = 5.1525

次に、毎日水やりをするすべての植物の平均高さを計算します。

1 日の平均 = (4.8 + 5 + 6.4 + 6.3 + … + 4.4 + 4.8 + 5.8 + 5.8) /20 = 5.155

次に、毎週水やりをしたすべての植物の平均高さを計算します。

週平均 = (4.4 + 4.9 + 5.8 + 6 + … + 3.9 + 4.8 + 5.5 + 5.5) /20 = 5.15

次に、次の式を使用して「水やりの頻度」係数の二乗和を計算します。

Σn(X _j – X ..) ²

金：

• n : グループ j のサンプルサイズ
• Σ : 「和」を意味するギリシャ語の記号
• X _j : グループ j の平均
• X .. : 大きな平均

この例では、「散水頻度」係数の二乗和を次のように計算します: 20(5.155-5.1525) ² + 20(5.15-5.1525) ² = 0.00025

ステップ 2: 2 番目の要素 (太陽光への曝露) の二乗和を計算します。

まず、40 個の植物の全体の平均高さを計算します。

全体の平均 = (4.8 + 5 + 6.4 + 6.3 + … + 3.9 + 4.8 + 5.5 + 5.5) / 40 = 5.1525

次に、太陽にさらされていないすべての植物の平均高さを計算します。

太陽なしの平均 = (4.8 + 4.4 + 3.2 + 3.9 + 4.4 + 4.4 + 4.2 + 3.8 + 3.7 + 3.9) / 10 = 4.07

この計算を繰り返して、さまざまな太陽光にさらされた植物の平均高さを求めます。

• 日照量が少ない場合の平均 = 5.1
• 平均平均日照量 = 5.89
• 平均日照量 = 5.55

次に、次の式を使用して「日光曝露」係数の二乗和を計算します。

Σn(X _j – X ..) ²

金：

• n : グループ j のサンプルサイズ
• Σ : 「和」を意味するギリシャ語の記号
• X _j : グループ j の平均
• X .. : 大きな平均

この例では、「日光曝露」係数の二乗和を次のように計算します: 10(4.07-5.1525) ² + 10(5.1-5.1525) ² + 10(5.89 -5.1525) ² + 10(5.55-5.1525) ² = 18.76475

ステップ 3: 内部の平方和を計算します (エラー)

次に、各因子の組み合わせと個々の草丈の差の二乗和を求めて二乗和を計算します。

たとえば、日光にさらさずに毎日水を与えたすべての植物の平均高さは 4.14 です。次に、これらの個々の植物の差の二乗和を次のように計算できます。

• 毎日の水やりと日光なしの SS: (4.8-4.14) ² + (4.4-4.14) ² + (3.2-4.14) ² + (3.9-4.14) ² + (4.4-4.14) ² = 1.512

要素の組み合わせごとにこのプロセスを繰り返すことができます。

• 毎日の水やりと日照不足の SS: 0.928
• 毎日の水やりと平均日照量のSS: 1,788
• 毎日の水やりと強い日差しのSS: 1.648
• 太陽が当たらない場合の毎週の水やりの SS: 0.34
• 毎週の水やりと日照不足の SS: 0.548
• 毎週の水やりと平均日照時間の SS: 0.652
• 毎週の水やりと強い日差しのSS： 1,268

次に、これらすべての値の合計を取得して、内部の二乗和を求めることができます (誤差)。

内の平方和 = 1.512 + 0.928 + 1.788 + 1.648 + 0.34 + 0.548 + 0.652 + 1.268 = 8.684

ステップ 4: 平方和の合計を計算する

次に、各植物の高さと総平均の差の合計を取ることで平方和の合計を計算できます。

二乗和の合計 = (4.8 – 5.1525) ² + (5 – 5.1525) ² + … + (5.5 – 5.1525) ² = 28.45975

ステップ 5: 相互作用二乗和を計算する

次に、次の式を使用して相互作用二乗和を計算します。

• 相互作用 SS = SS 合計 – SS ファクター 1 – SS ファクター 2 – SS 内部
• SS 相互作用 = 28.45975 – 0.00025 – 18.76475 – 8.684
• SS 相互作用 = 1.01075

ステップ 6: ANOVA 表を完成させる

最後に、二元配置分散分析テーブルの値を入力します。

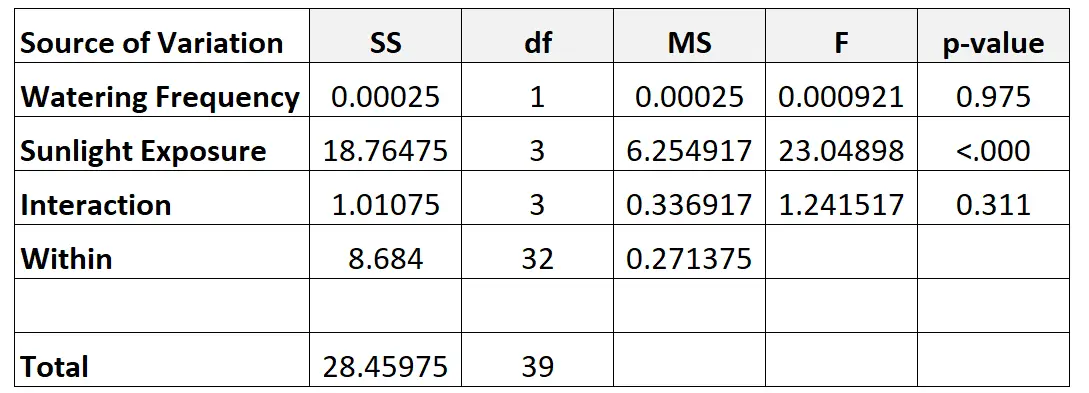
表内のさまざまな数値を計算する方法は次のとおりです。

• df 水やり頻度: d-1 = 2-1 = 1
• df 太陽光への曝露: k-1 = 4-1 = 3
• dfInteraction : (j-1)*(k-1) = 1*3 = 3
• df In : n – (j*k) = 40 – (2*4) = 32
• 合計DF: n-1 = 40-1 = 39
• MS： SS/DF
• 散水頻度 F : 屋内 MS/MS 散水頻度
• F 太陽光への曝露: MS / MS 屋内での太陽光曝露
• インタラクション F : インタラクション MS / MS 内
• p 値散水頻度: 分子 df = 1、分母 df = 32 の F 値 0.000921 に対応する p 値
• 太陽光露出の p 値: 分子 df = 3、分母 df = 32 の F 値 23.04898 に対応する p 値
• p 値相互作用: 分子 df = 3、分母 df = 32 の F 値 1.241517 に対応する p 値。

注 #1: n = 観察の総数、j = 水やり頻度のレベル数、k = 日光曝露のレベル数。

注#2 : F 値に対応する p 値は、F 分布計算機を使用して計算されました。

ステップ 7: 結果を解釈する

ANOVA 表から次のことがわかります。

• 水やりの頻度と日光への曝露の間の相互作用の p 値は0.311でした。 α = 0.05 では、これは統計的に有意ではありません。
• 水やり頻度の p 値は0.975でした。 α = 0.05 では、これは統計的に有意ではありません。
• 日光曝露の p 値は<0.000でした。これは、α = 0.05 で統計的に有意です。

これらの結果は、日光への曝露が草丈に統計的に有意な影響を与える唯一の要因であることを示しています。

また、相互作用効果がないため、日光曝露の影響は水やり頻度の各レベルで一貫しています。

簡単に言えば、植物に毎日水やりをするか毎週水をやるかは、日光への曝露が植物に与える影響には影響しません。

追加リソース

次のチュートリアルでは、ANOVA に関する追加情報を提供します。

一元配置分散分析を手動で実行する方法
反復測定 ANOVA を手動で実行する方法
完全ガイド: 二元配置分散分析結果をレポートする方法