手動による多重線形回帰 (ステップバイステップ)
重線形回帰は、 2 つ以上の予測変数と応答変数の間の関係を定量化するために使用できる方法です。
このチュートリアルでは、多重線形回帰を手動で実行する方法について説明します。
例: 手動による重回帰
応答変数yと 2 つの予測子変数 x 1および x 2を含む次のデータセットがあるとします。
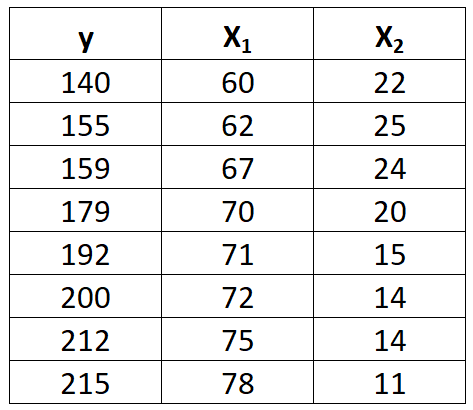
重線形回帰モデルをこのデータセットに適合させるには、次の手順を実行します。
ステップ 1: x 1 2 、x 2 2 、x 1 y、x 2 y、および x 1 x 2を計算します。
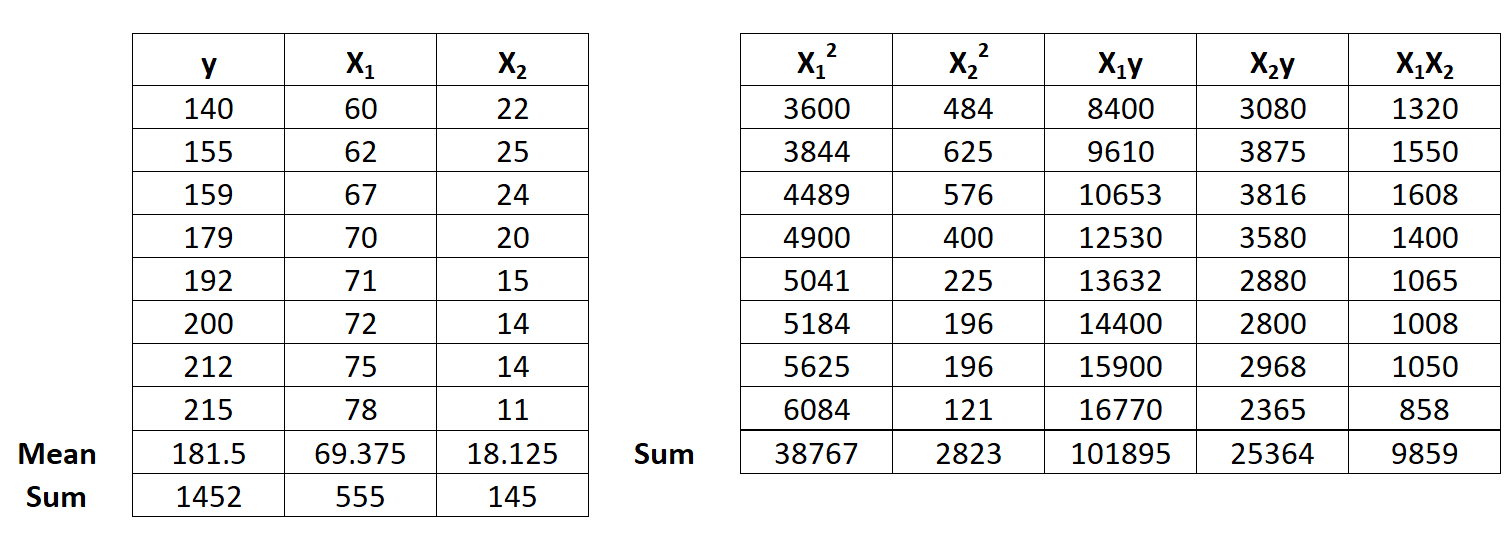
ステップ 2: 回帰合計を計算します。
次に、次の回帰合計の計算を実行します。
- Σx12 = ΣX12 – ( ΣX1 ) 2 / n = 38.767 – (555) 2 / 8 = 263.875
- Σx22 = ΣX22 – ( ΣX2 ) 2 / n = 2823 – (145) 2 / 8 = 194.875
- Σ x 1 y = Σ
- Σ × 2y = Σ
- Σ × 1 × 2 = Σ
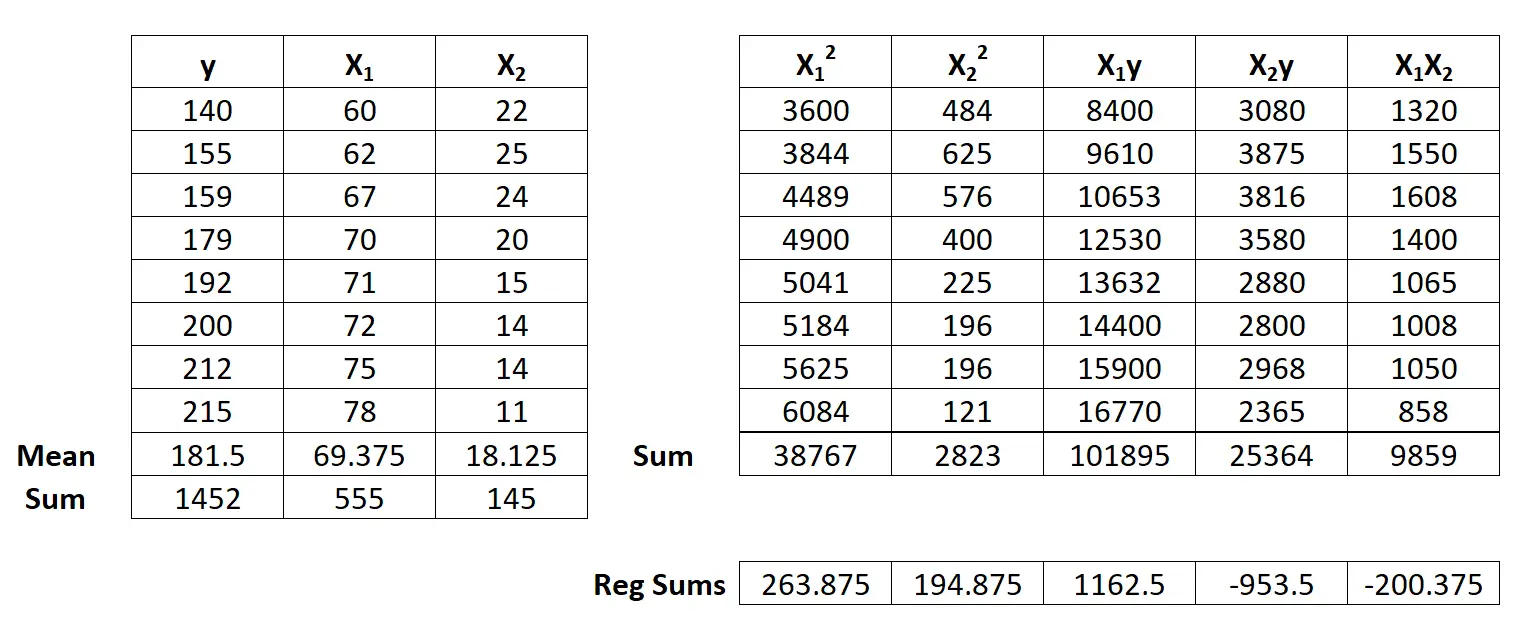
ステップ 3: b 0 、b 1 、および b 2を計算します。
b 1を計算する式は次のとおりです: [(Σx 2 2 )(Σx 1 y) – (Σx 1 x 2 )(Σx 2 y)] / [(Σx 1 2 )(Σx 2 2 ) – (Σx 1 x 2) ) 2 ]
したがって、 b 1 = [(194.875)(1162.5) – (-200.375)(-953.5)] / [(263.875) (194.875) – (-200.375) 2 ] = 3.148
b 2を計算する式は次のとおりです: [(Σx 1 2 )(Σx 2 y) – (Σx 1 x 2 )(Σx 1 y)] / [(Σx 1 2 )(Σx 2 2 ) – (Σx 1 x 2) ) 2 ]
したがって、 b 2 = [(263.875)(-953.5) – (-200.375)(1152.5)] / [(263.875) (194.875) – (-200.375) 2 ] = -1.656
b 0を計算する式は次のとおりです: y – b 1 X 1 – b 2 X 2
したがって、 b 0 = 181.5 – 3.148(69.375) – (-1.656)(18.125) = -6.867
ステップ 5: b 0 、b 1 、および b 2を推定された線形回帰式に代入します。
推定される線形回帰式は次のとおりです: ŷ = b 0 + b 1 *x 1 + b 2 *x 2
この例では、 ŷ = -6.867 + 3.148x 1 – 1.656x 2となります。
重回帰式を解釈する方法
この推定線形回帰式を解釈する方法は次のとおりです: ŷ = -6.867 + 3.148x 1 – 1.656x 2
b0 = -6.867 。両方の予測子変数がゼロに等しい場合、y の平均値は -6.867 です。
b1 = 3.148 。 x 2 が一定のままであると仮定すると、x 1の1 単位の増加は、平均して y の 3.148 単位の増加に関連付けられます。
b2 = -1.656 。 x 1 が一定のままであると仮定すると、x 2の1 単位の増加は、平均して y の 1,656 単位の減少に関連します。
追加リソース
重線形回帰の概要
単純な線形回帰を手動で実行する方法