Excelで指数分布を使用する方法
指数分布は、特定のイベントが発生するまで待機する時間をモデル化するために使用される確率分布です。
この分布は、次のような質問に答えるために使用できます。
- 小売業者は顧客が店舗に入るまでどれくらい待つ必要がありますか?
- バッテリーはどれくらいの時間使い続ければ切れますか?
- コンピュータは壊れるまでどれくらいの期間動作し続けるでしょうか?
各シナリオで、特定のイベントが発生するまで待機する必要がある時間を計算したいと考えています。したがって、各シナリオは指数分布を使用してモデル化できます。
確率変数X が指数分布に従う場合、 Xの累積密度関数は次のように書くことができます。
F (x; λ) = 1 – e -λx
金:
- λ:速度パラメータ (λ = 1/μ として計算)
- e: 2.718 にほぼ等しい定数
Excel で指数分布の累積密度関数に関連する確率を計算するには、次の式を使用できます。
=EXPON.DIST(x, lambda, cumulative)
金:
- x : 指数関数的に分布した確率変数の値
- lambda : レートパラメータ
- cumulative : 累積密度関数を使用するかどうか (TRUE または FALSE)
次の例は、この公式を実際に使用する方法を示しています。
例1: 次の顧客が到着するまでの時間
平均して 2 分ごとに新しい顧客が店舗に入ります。顧客が到着した後、1 分以内に新しい顧客が到着する確率を決定します。
解決策:顧客間の平均時間は 2 分です。したがって、レートは次のように計算できます。
- λ = 1/μ
- λ = 1/2
- λ = 0.5
したがって、Excel で次の数式を使用して、1 分以内に新規顧客が到着する確率を計算できます。
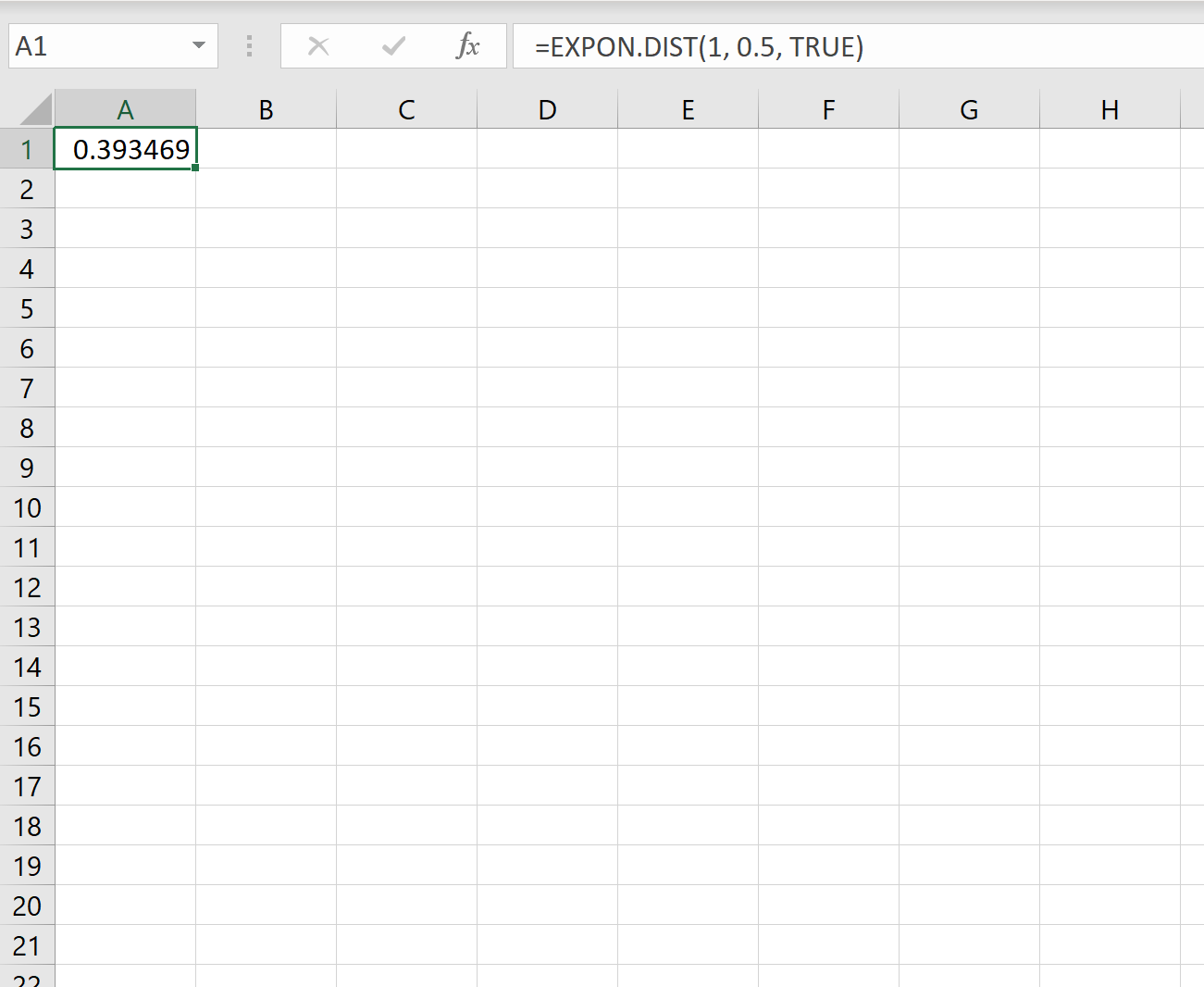
次の顧客が到着するまでに 1 分未満待たなければならない確率は0.393469です。
例 2: 次の地震までの時間
ある地域で平均 400 日ごとに地震が発生するとします。地震の後、次の地震が発生するまでに 500 日以上かかる確率を求めます。
解決策:地震の平均間隔は 400 日です。したがって、レートは次のように計算できます。
- λ = 1/μ
- λ = 1/400
- λ = 0.0025
したがって、Excel で次の式を使用して、次の地震が発生するまでに 500 日未満かかる確率を計算できます。
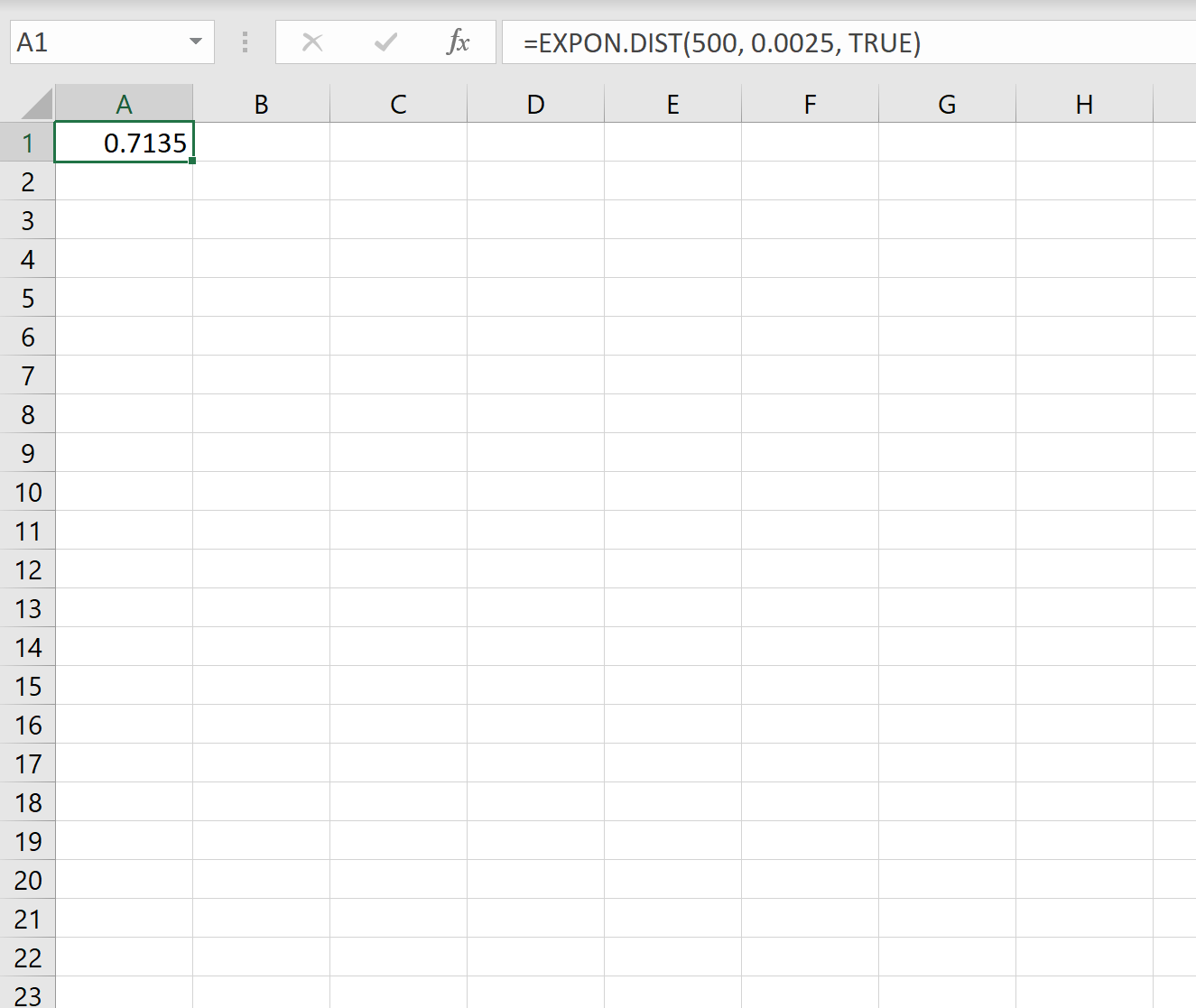
次の地震まで 500 日以内に起こる確率は 0.7135 です。
したがって、次の地震まで 500 日以上待たなければならない確率は 1 – 0.7135 = 0.2865となります。
例 3: 次の電話までの時間
コールセンターが平均して 10 分ごとに新しい電話を受けるとします。顧客からの電話後、10 ~ 15 分以内に新しい顧客から電話がかかる可能性を判断します。
解決策:通話間の平均時間は 10 分です。したがって、レートは次のように計算できます。
- λ = 1/μ
- λ = 1/10
- λ = 0.1
したがって、Excel で次の数式を使用して、次の顧客が 10 ~ 15 分以内に電話をかける確率を計算できます。
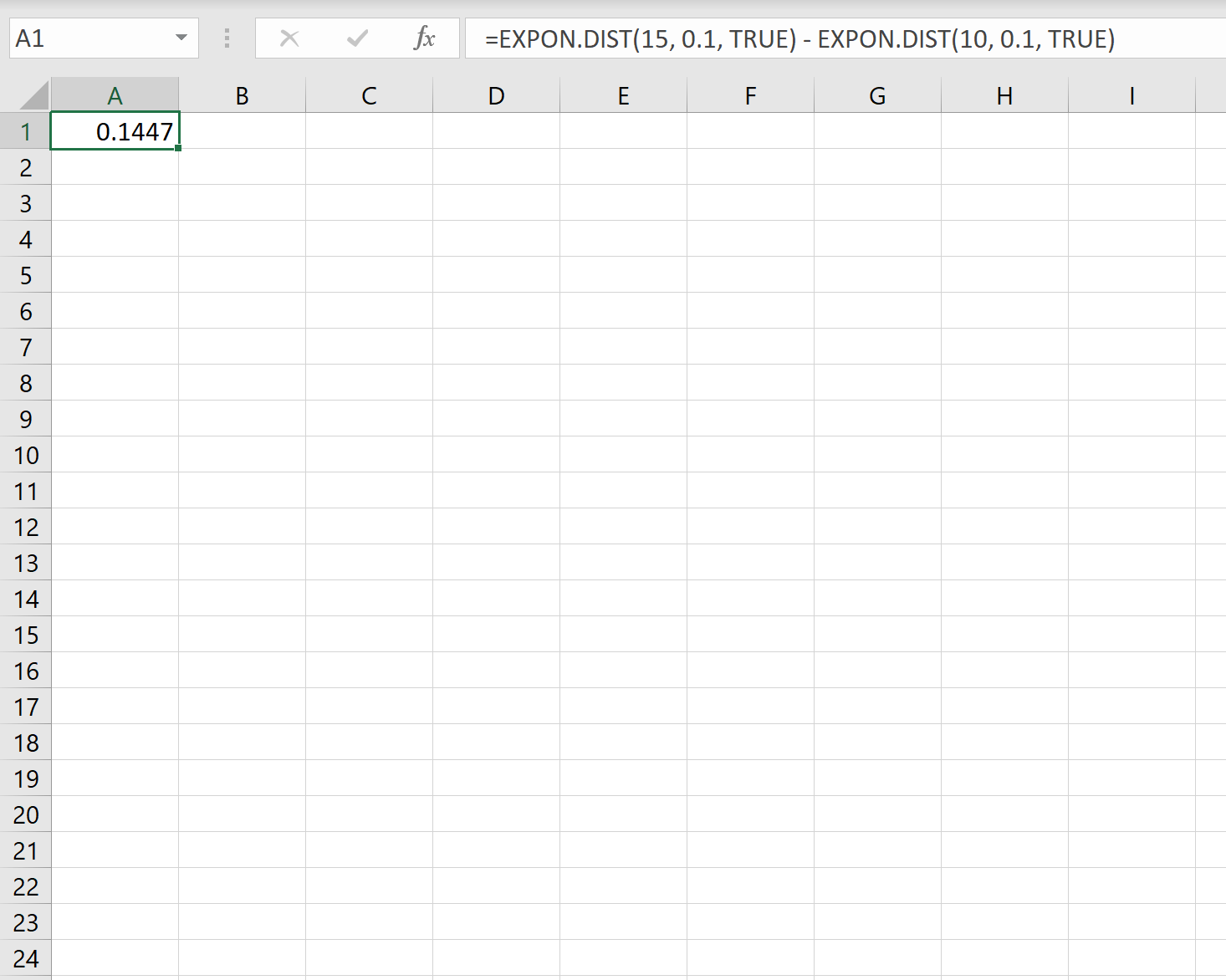
新規顧客から 10 ~ 15 分以内に電話がかかる可能性。は0.1447です。