条件付き確率 (または条件付き確率)

ここでは、条件付き確率（または条件付き確率）とは何かを確認します。条件付き確率の計算方法と、このタイプの確率の特性を例に説明します。さらに、段階的に解かれた条件付き確率の演習を練習することができます。

条件付き確率とは何ですか?

条件付き確率 は、条件付き確率とも呼ばれ、別のイベント B が発生した場合にイベント A が発生する確率を示す統計的尺度です。つまり、条件付き確率 P(A|B) は、イベント B がすでに発生した後にイベント A が発生する確率を指します。

条件付き確率は、2 つのイベント間の垂直バーで書かれます: P(A|B)、「イベント B が与えられた場合のイベント A の条件付き確率」となります。

条件付き確率の値は 0 から 1 までの数値であることに注意してください。条件付き確率が高いほど、イベント B が発生したときにイベント A が発生する可能性が高くなりますが、条件付き確率が低いほど、イベント A が発生する可能性は低くなります。イベントBが発生すると発生します。

条件付き確率の式

イベント B が与えられた場合のイベント A の条件付き確率は、イベント A とイベント B の交差の確率をイベント B の確率で割ったものに等しくなります。

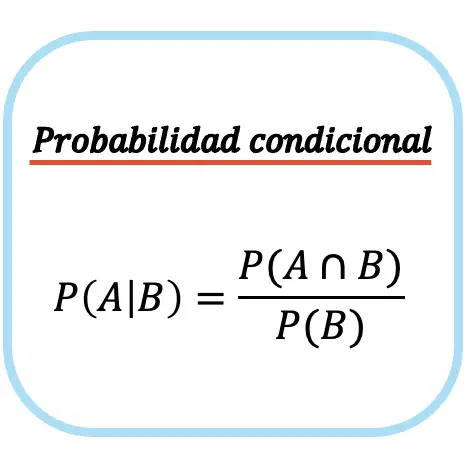
条件付き確率 (または条件付き確率) の公式は、無条件イベントの発生確率がゼロでない場合、つまり P(B) ≠ 0 の場合にのみ使用できることに注意してください。言い換えれば、イベント B が発生する可能性がある場合。

条件付き確率はその逆関数から計算することもできます。つまり、P(B|A) が既知であれば、P(A|B) を決定できます。ただし、これを行うには、ベイズの定理を適用する必要があります。この定理の構成をここで確認できます。

条件付き確率の例

条件付き確率の定義と公式が何であるかを理解したら、このタイプの確率の例を段階的に解き、その意味を完全に理解します。

• 30 人の生徒のクラスで試験を受けた後、何人の生徒が勉強し、何人が合格したかを調べるデータが収集されました。結果は次の分割表に示されています。収集したデータから、すでに勉強している場合に試験に合格する条件付き確率を計算します。

条件付き確率を取得するには、前に見た公式を適用する必要があります。

したがって、まず学生が勉強して勉強して合格した確率を見つける必要があります。学生が勉強した確率を求めるには、ラプラスの法則を使用するだけです。つまり、勉強した学生の数を観測値の総数で割ります。

そして、勉強して合格した生徒の数を合計で割ることにより、分割表から生徒が同時に勉強して合格した確率を求めることができます。

したがって、学生が勉強した場合に試験に合格する確率は次のようになります。

依存イベントと独立イベントの条件付き確率

このセクションでは、条件付き確率と依存イベントと独立イベント (または依存イベントと独立イベント) の間にどのような関係があるのかを見ていきます。なぜなら、これら 2 種類のイベントは異なる概念ではありますが、条件付き確率に関連付けられているからです。

2 つのイベント (または発生) は、発生確率が互いに依存しない場合、独立しています。このような場合、2 つのイベント間の交差は、各イベントの個別の確率の積と等価になります。したがって、条件付き確率の式は次のように簡略化されます。

つまり、イベント A と B が独立している場合、イベント B が与えられた場合のイベント A の条件付き確率は、イベント A が発生する確率とまったく同じになります。

一方、2 つのイベントが依存関係にある場合、一方のイベントの確率がもう一方のイベントの確率に依存することを意味します。したがって、 2 つのイベント A と B が依存関係にある場合、イベント B が与えられた場合のイベント A の条件付き確率は、イベント A の発生確率とは異なります。

条件付き確率の演習を解決しました

演習 1

ボールがいっぱい入った袋の中では、半分はオレンジ色、残りの半分は緑色であることがわかります。さらに、すべてのボールの 3 分の 1 はオレンジ色であり、同時にサインが付いています。オレンジ色のボールを引いたときに信号を受信する確率はどれくらいですか?

この演習を解くには、次の条件式確率を適用する必要があります。

問題文は、袋の半分がオレンジであることを示しています。したがって、オレンジ色のボールを拾う理論上の確率は 50% です。

一方、全体の 3 分の 1 はオレンジ色のボールであり、シグナルがあることがわかっているため、シグナルのあるオレンジ色のボールを取得する確率は次のようになります。

最後に、計算された確率を条件付き確率の式に代入して、その値を求めます。

要約すると、オレンジ色のシグナルでボールを引く確率は 66% です。

演習 2

箱の中に 6 本の青ペンと 3 本の黒ペンがある場合、1 本の青ペンを引く確率と 2 本の青ペンを連続して引く確率を計算します。

青いペンを 1 回拾う確率を求めるには、単純にラプラスの法則を使用します。

この問題では、2 本の青ペンを連続して拾う確率、つまり、以前に青ペンを拾ったことがある場合に青ペンを拾う条件付き確率を知ることも求められます。

青のペンを引くと、状況はあまり有利ではなくなりますが、合計ではペンが 1 本減ります。したがって、条件付き確率は次のようになります。

演習 3

コイントスの結果が表の場合、サイコロを振って数字が 4 になる条件付き確率はいくらですか?

この演習を解くには、条件付き確率の理論を考慮する必要があります。これは、「サイコロを投げて 4 の目を得る」イベントと「コインを投げて表を得る」イベントは独立しているためです。したがって、条件付き確率の式を使用する必要はありませんが、次の等式が満たされます。

したがって、条件付き確率を求めるには、単純にラプラスの法則を使用します。

演習 4

ある国の 25 社の会計年度と、その年の経済結果に応じて株価がどのように変化するかを調査しました。収集されたデータは次の分割表で確認できます。

過去 1 年間に利益が出た場合、その企業の株価が上昇する可能性はどのくらいですか?

この演習では、企業が経済的にプラスの成果を達成した場合に株価が上昇する条件付き確率について尋ねます。したがって、この確率を計算するには、条件付き確率の公式を使用する必要があります。

したがって、最初に企業が利益を得る確率を計算し、次に企業が 1 株当たりの価格を上昇させながら経済的利益を得る確率を計算します。

そして、見つかった値を式に代入し、条件付き確率を計算します。

条件付き確率の性質

条件付き確率、または条件付き確率のプロパティは次のとおりです。

• イベント B が与えられた場合のイベント A の条件付き確率と、イベント B が与えられた場合の補足イベント A の条件付き確率の合計は 1 に等しくなります。

• イベント A がイベント B のサブセットである場合、B が true の場合、A は常に発生します。したがって、これらの場合、イベント B が与えられた場合のイベント A の条件付き確率は 1 です。

• 2 つの異なるイベントが与えられた場合、条件付き確率に関して次の等式が常に成り立ちます。