セットの演算: 和集合、積集合、補数、差分
セットとは要素の集合です。
セットを大文字で指定し、中括弧を使用してセットの要素を定義します。たとえば、要素 1、2、3 を持つ「A」というセットがあるとします。これを次のように記述します。
A = {1、2、3}
このチュートリアルでは、確率と統計で最も一般的に使用される集合演算について説明します。
連合
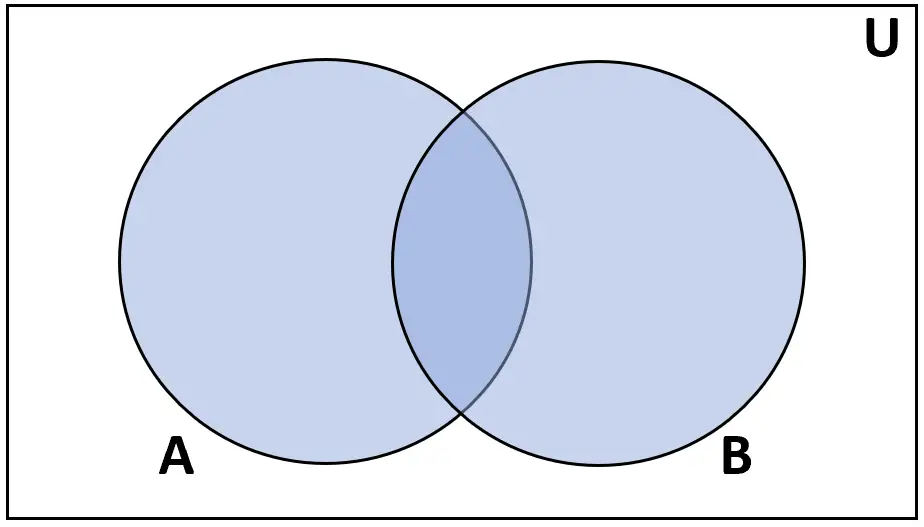
定義:セット A と B の和集合は、A または B のいずれかにある要素のセットです。
評価: A ∪ B
例:
- {1, 2, 3} ∪ {4, 5, 6} = {1, 2, 3, 4, 5, 6}
- {1, 2} ∪ {1, 2} = {1, 2}
- {1, 2, 3} ∪ {3, 4} = {1, 2, 3, 4}
交差点
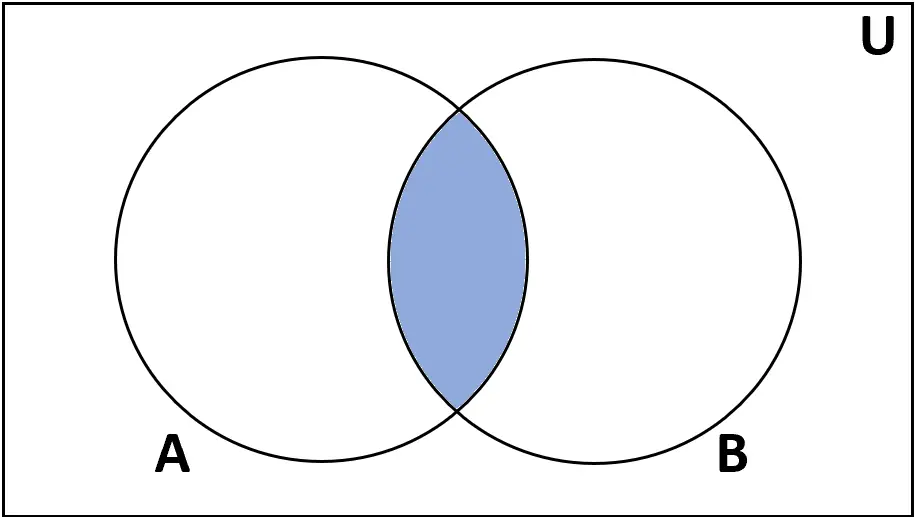
定義:セット A と B の共通部分は、A と B の両方にある要素のセットです。
表記: A ∩ B
例:
- {1, 2, 3} ∩ {4, 5, 6} = {∅}
- {1, 2} ∩ {1, 2} = {1, 2}
- {1, 2, 3} ∩ {3, 4} = {3}
補体
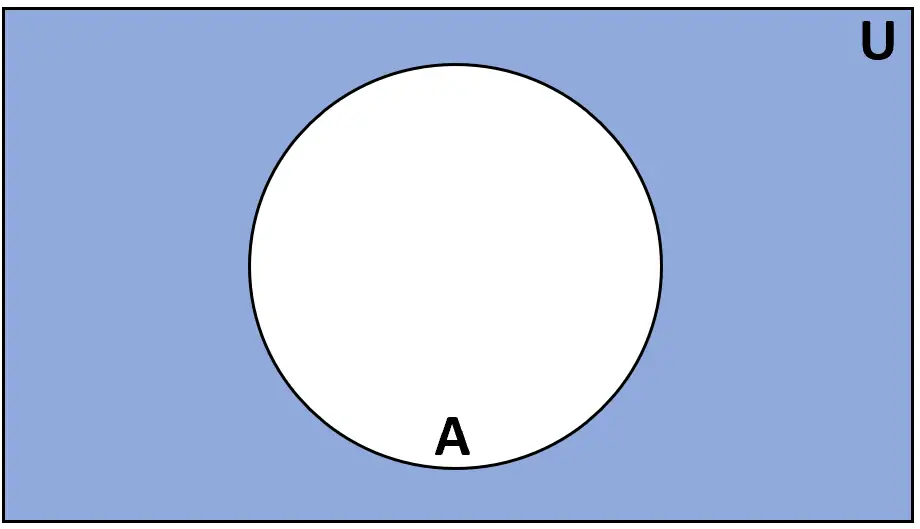
定義:集合 A の補集合は、普遍集合 U にはあるが A には存在しない要素の集合です。
評価: A’ またはAc
例:
- U = {1, 2, 3, 4, 5, 6} かつ A = {1, 2} の場合、A c = {3, 4, 5, 6}
- U = {1, 2, 3} かつ A = {1, 2} の場合、A c = {3}
違い
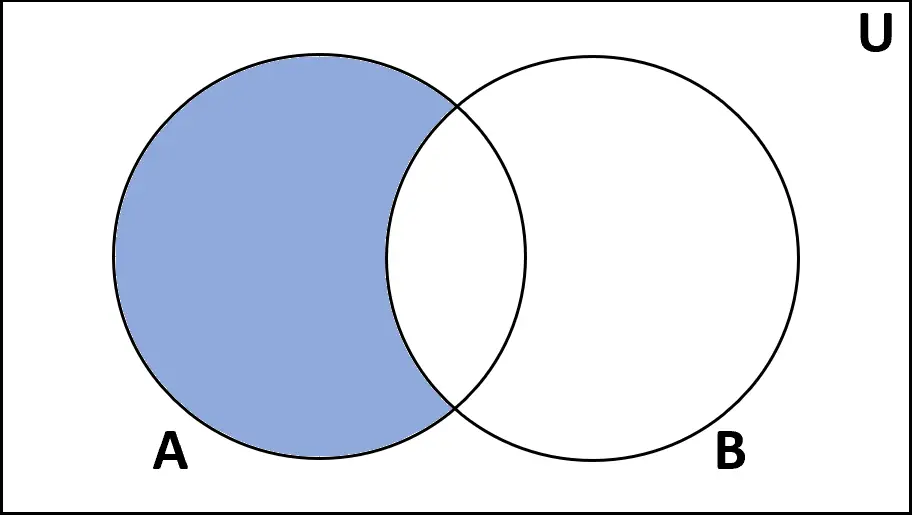
定義:セット A と B の違いは、A にはあるが B には存在しない要素のセットです。
評価: A ~ B
例:
- {1、2、3} – {2、3、4} = {1}
- {1, 2} – {1, 2} = {∅}
- {1、2、3} – {4、5} = {1、2、3}
対称的な差異
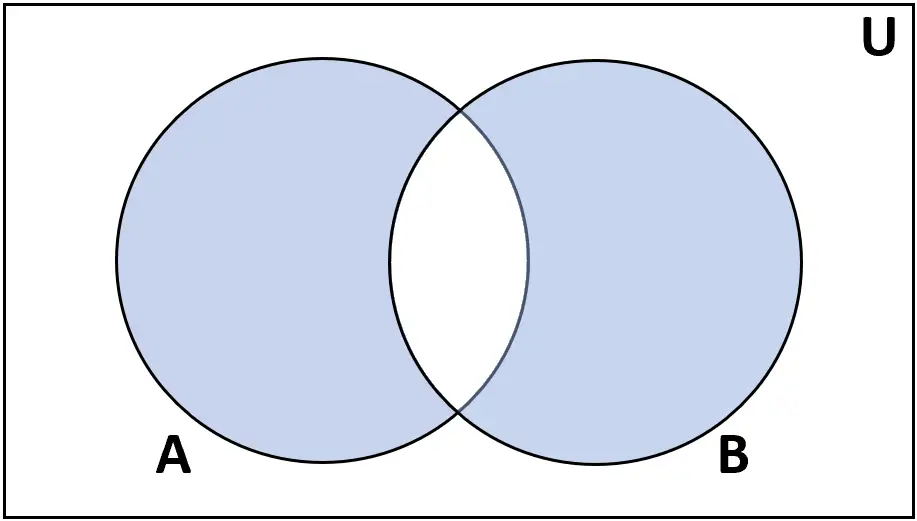
定義:セット A と B の対称的な違いは、 A または B のどちらかに存在するが、両方には存在しない要素のセットです。
評価: AΔB
例:
- {1, 2, 3} Δ {2, 3, 4} = {1, 4}
- {1, 2} Δ {1, 2} = {∅}
- {1, 2, 3} Δ {4, 5} = {1, 2, 3, 4, 5}
デカルト積
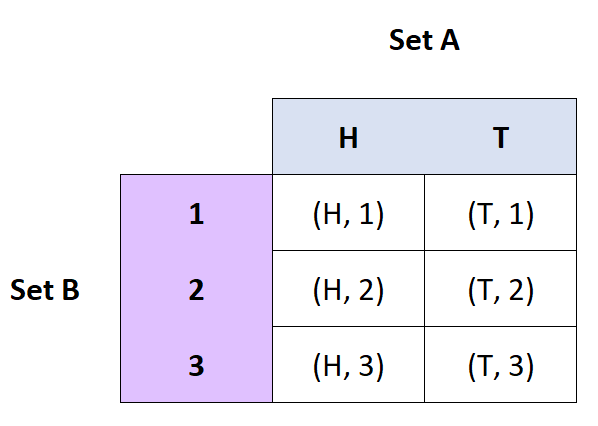
定義:集合 A と B のデカルト積は、A と B の順序付きペアの集合です。
評価: A × B
例:
- A = {H, T} および B = {1, 2, 3} の場合、A x B = {(H, 1), (H, 2), (H, 3), (T, 1), ( T、2)、(T、3)}
- A = {T, H} および B = {1, 2, 3} の場合、A x B = {(T, 1), (T, 2), (T, 3), (H, 1), ( H、2)、(H、3)}